the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Monitoring of induced distributed double-couple sources using Marchenko-based virtual receivers
Joeri Brackenhoff
Jan Thorbecke
Kees Wapenaar
We aim to monitor and characterize signals in the subsurface by combining these passive signals with recorded reflection data at the surface of the Earth. To achieve this, we propose a method to create virtual receivers from reflection data using the Marchenko method. By applying homogeneous Green’s function retrieval, these virtual receivers are then used to monitor the responses from subsurface sources. We consider monopole point sources with a symmetric source signal, for which the full wave field without artifacts in the subsurface can be obtained. Responses from more complex source mechanisms, such as double-couple sources, can also be used and provide results with comparable quality to the monopole responses. If the source signal is not symmetric in time, our technique based on homogeneous Green’s function retrieval provides an incomplete signal, with additional artifacts. The duration of these artifacts is limited and they are only present when the source of the signal is located above the virtual receiver. For sources along a fault rupture, this limitation is also present and more severe due to the source activating over a longer period of time. Part of the correct signal is still retrieved, as is the source location of the signal. These artifacts do not occur in another method that creates virtual sources as well as receivers from reflection data at the surface. This second method can be used to forecast responses to possible future induced seismicity sources (monopoles, double-couple sources and fault ruptures). This method is applied to field data, and similar results to the ones on synthetic data are achieved, which shows the potential for application on real data signals.
- Article
(10884 KB) - Full-text XML
-
Supplement
(364 KB) - BibTeX
- EndNote
Seismic monitoring of processes in the subsurface has been an active field of research for many years. Traditionally, most recording setups are limited to the surface of the Earth, although boreholes can also be utilized. The latter approach is more expensive and complicated, however. In the case of monitoring with active sources, the receivers in these recording setups measure valuable reflection data, which provide quantifiable information about processes in the subsurface. Some examples of using this information are monitoring time shifts in seismic data to predict the velocity–strain relation for a depleting reservoir (Hatchell and Bourne, 2005) and the monitoring of geomechanics in the subsurface by using time-lapse data (Herwanger and Horne, 2009). The responses from passive sources, such as when the signal is caused by an induced earthquake, can be measured as well. These passive measurements are more difficult to process due to the fact that the signal is complex and unknown (McClellan et al., 2018); however, the information content in these induced seismic signals is of great interest. Induced seismicity has had a large impact in countries such as the Netherlands (van Thienen-Visser and Breunese, 2015) and the USA (Magnani et al., 2017), and there is much discussion about the cause and the effects. To determine the cause of induced seismicity, the source of the signal is of particular interest, and consequently inversions for the source mechanism (Zhang and Eaton, 2018) as well as the location of the source (Eisner et al., 2010) are often performed. These methods can be carried out from surveys that are located at the surface of the Earth or inside boreholes; however, they are limited in accuracy. Ideally, one would use a dense network of receivers around the source location to directly monitor the wave field.
Due to practical difficulties and expenses associated with placing a dense network of receivers in the subsurface, the wave field generally cannot be directly measured around the source location of the signal. An alternative to using physical receivers for these measurements is the use of virtual receivers. A virtual receiver is not physically present in the subsurface; rather, it is created through processing measured signals at the surface. Virtual receivers can be created in a variety of ways. A mathematical basis for the retrieval of these virtual receivers is the so-called homogeneous Green's function representation. The classical form of this representation was proposed by Porter (1970) and extended for inverse source problems by Porter and Devaney (1982) and for inverse scattering methods by Oristaglio (1989). This representation states that if the responses from two signals are measured on an enclosing recording surface, the response between the two sources of the signals can be retrieved. It forms the basis for seismic interferometry to create virtual sources (Wapenaar et al., 2005) or virtual receivers (Curtis et al., 2009). All of these approaches require access to the medium from an enclosing surface and introduce artifacts if this requirement is not met. Even though this limitation is well known, for many cases these approaches are still utilized.
A novel approach that can be used when the acquisition surface is not closed is the data-driven 3-D Marchenko method. This method can create virtual sources and receivers in the subsurface (Wapenaar et al., 2014; Slob et al., 2014). In order to achieve this, the method requires a reflection response recorded at the surface of the Earth and an estimation of the first arrival of the signal from a location in the subsurface to the receiver locations in the measurement array. This first arrival can be estimated from a background velocity model, which requires no detailed information about the subsurface. Through the Marchenko method, the Green's function with a virtual receiver in the subsurface can be retrieved. Using this method, many virtual receivers can be created in the subsurface, which can be used to monitor the wave field from the virtual receiver locations to the receiver array. To obtain the signal between an induced signal from the subsurface and the virtual receiver locations, homogeneous Green's function retrieval can be employed; however, as pointed out before, the classical retrieval scheme would include artifacts due to the open surface of the recording. These artifacts can disturb the interpretation of the signal. An alternative retrieval scheme was developed by Wapenaar et al. (2016), who showed that if a focusing function is used in combination with a Green's function, an open surface can be used for the retrieval instead of an enclosing one, without the artifacts of the classical method when applied to an open surface. A focusing function is a wave field that is designed to focus at a location in the subsurface and can be retrieved from reflection data using the Marchenko method (van der Neut et al., 2015). This single-sided representation has been proven to work successfully on both synthetic data and on field data (Brackenhoff et al., 2019).
Using the single-sided method, two approaches for monitoring induced seismicity can be taken. First, virtual receivers can be used in combination with a virtual source. In this case, all the signals are created from the reflection data using the Marchenko method. This has the benefit that the virtual source can be created at any location in the subsurface, where one expects induced seismicity to happen, and that the source signal can be controlled. This is the way that the method has been mostly applied in previous works. Another approach that can be taken is to create virtual receivers using the Marchenko method and to use a real induced seismic source signal instead of a virtual Green's function. This effectively allows for the monitoring of the actual signal in the subsurface, including the source location and mechanism. This could be a boon to induced seismicity monitoring; however, this approach does require some modifications. Induced seismicity often causes more complex source signals that evolve over a period of time and cover an extended area in the subsurface. These rupture planes or fault sources are the main topic of interest.
In this work, we aim to apply the single-sided homogeneous Green's function retrieval on both synthetic and field data for a distribution of virtual double-couple sources. We first apply the method on synthetic data for point sources and show the principles of the representation. We then use the same synthetic data to apply the representation with modifications to the sources originating from a fault plane and show the results that can be achieved. Finally, we also apply the representation on field data for both types of sources.
2.1 Green's function and focusing function
In this paper, we present several representations for the retrieval of wave fields in the subsurface. First, we review the properties and quantities that are relevant for these representations. To this end, we consider a medium that is acoustic, lossless and inhomogeneous with mass density ρ(x) and compressibility κ(x), where indicates the Cartesian coordinate vector. We make use of a Green's function in this medium that obeys the following wave equation:
where indicates a Green's function that at time t describes the response of the medium at location x due to a unit impulsive point source of volume-injection rate density δ(x−xA)δ(t) at source location xA. δ(⋅) is the Dirac delta function, ∂t the temporal partial differential operator and ∂i a component of a vector containing the spatial partial differential operators in the three principal directions . Einstein's summation convention applies to repeated subscripts. The Green's function obeys source–receiver reciprocity, which allows for the interchange of the source and receiver position; hence, . We impose causality on the Green's function, for t<0, such that it is forward propagating, originating from the source and a causal solution to Eq. (1). A schematic illustration of the Green's function is shown in Fig. 1a, where several possible ray paths are drawn for a heterogeneous model. This includes the direct arrival, primary reflections and multiple reflections.
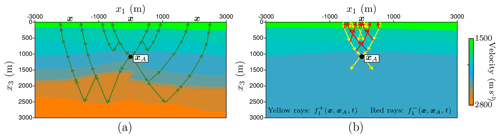
Figure 1(a) Schematic representation of the Green's function , defined in the physical medium, with a source located at xA, which is measured at a varying location x at the surface. (b) Schematic representation of the focusing function , defined in the truncated medium, where the wave field propagates from x at the surface to the focal location xA. For both functions, several possible ray paths are drawn. For the focusing function the downgoing waves are marked with yellow arrows and the upgoing waves with red arrows.
We also consider the time-reversed Green's function , which is the acausal solution to Eq. (1), where the causality condition implies for t>0. Superposition of the causal and acausal Green's function yields the homogeneous Green's function:
where obeys the homogeneous wave equation,
Equation (3) is similar to Eq. (1), with the exception of the lack of a source singularity on the right-hand side of the equation.
Aside from the Green's function, we consider the focusing function , which describes a wave field at time t and location x, that converges to a focal location xA in the subsurface of a medium that is truncated below the focal location. The focusing function can be decomposed as
where denotes the downgoing and the upgoing component of the focusing function. A schematic representation of the focusing function can be found in Fig. 1b. Similar to the Green's function, several possible ray paths are drawn; however, to distinguish the decomposed wave fields, the downgoing focusing function is marked with yellow rays and the upgoing focusing function with red rays. The medium of the focusing function and the Green's function are identical until the focal depth, after which the medium of the focusing function becomes truncated. The physical and truncated medium can be used in reciprocity theorems in order to relate the focusing function to the Green's function, which is shown in Sect. S2 of the Supplement. For moderately inhomogeneous media, the focusing function and Green's function can be separated from each other in time. The coda of the focusing function resides in the interval between the direct arrival of a related Green's function and its time reversal. The direct arrival of the focusing function coincides with the direct arrival of the time-reversed Green's function. This difference in time intervals explains some of the effects that are present in the representations that are used in this paper. Both the focusing function and Green's function can be retrieved for a heterogeneous medium from the reflection data and an estimate of the direct arrival through use of the Marchenko method. We will not explain this method in detail in this paper; instead, we refer the reader to Wapenaar et al. (2014) for a more detailed overview.
Due to the nature of some equations, we also make use of the frequency domain version of the time domain quantities. To obtain these transformations we make use of the Fourier transform. We define the Fourier transform of a space- and time-dependent function u(x,t) as
where u(x,ω) is the Fourier-transformed version of u(x,t) in the space-frequency domain, with ω as the angular frequency and i the imaginary unit. By using Eq. (5) we obtain the space-frequency domain versions of Eqs. (1), (2), (3) and (4) as
respectively, where ℜ indicates the real part of a complex function.
2.2 Homogeneous Green's function representation
The classical homogeneous Green's function representation was originally developed for a configuration in which the Green's function was measured on an arbitrarily shaped surface enclosing the medium of interest (Porter, 1970; Porter and Devaney, 1982; Oristaglio, 1989). The representation states that if the responses from two sources inside the medium are recorded on the surface, the response between the two source locations can be obtained. For seismic recording setups, the measurements are usually only available at the surface of the Earth, meaning that the surface is single-sided instead of closed, which will introduce significant errors into the final result.

Figure 2Setup for the single-sided Green's function representation for (a) a case in which the source of the Green's function is located below the focal location and (b) a case in which the source of the Green's function is located above the focal location. The rays in this figure indicate full Green's functions and focusing functions, including multiple scattering.
In recent years a new representation for homogeneous Green's function retrieval was developed that is designed to work with the single-sided surface, whereby a focusing function is used together with a Green's function (Wapenaar et al., 2016). Consider the setup in Fig. 2, where a heterogeneous medium 𝕍A is bounded by two horizontal surfaces 𝕊0 and 𝕊A on two different levels in the vertical direction x3. The surfaces extend infinitely in the horizontal directions x1 and x2. The medium above 𝕊0 is homogeneous, with mass density ρ0 and compressibility κ0, and the surface itself is nonreflecting, while the medium below 𝕊A can be heterogeneous. The upper surface 𝕊0 corresponds to the surface where the receiver locations x of the focusing functions and Green's functions are available. In this scenario, we assume that we have three functions available at the upper surface: a Green's function that has a source location below 𝕊A, a Green's function that has a source location inside medium 𝕍A and a focusing function that has a focal location xA located at the depth of 𝕊A.
The available functions can be used to obtain the response between two locations. To this end, we use the representation given by Eq. (35) of the Supplement (for the derivation see Sect. 2.3 of the Supplement):
where ℑ is the imaginary part of a complex function and χ(xB) is the characteristic function
This representation states that by applying the focusing function components to a Green's function at the upper surface, the Green's function between the focal location xA of the focusing function and the source location xB of the Green's function can be obtained. The focal location will become the receiver of this new Green's function, and the source location of the original Green's function on the right-hand side of Eq. (10) will become the source location of the new Green's function. However, contributions from the imaginary part of the focusing function between the source and receiver locations are present if the source location is located inside the medium 𝕍A, as is the case if the Green's function from Fig. 2b with source location is used. Because they are related to a focusing function, these artifacts will be present between the direct arrival of the Green's function and its time reversal. In this case, the source location is present above the focal location. These contributions vanish if the source location is present outside 𝕍A, in other words if it is located below the focal location, such as when the Green's function from Fig. 2a with source location is used. This would mean that without knowledge of , we are limited in the correct application of the representation. To overcome this limitation, we substitute Eq. (10) into the right-hand side of Eq. (7) to create the single-sided homogeneous Green's function representation:
which corresponds to Eq. (33) from our companion paper (Wapenaar et al., 2019). The additional contributions have vanished from this representation, and the homogeneous Green's function will be obtained when it is evaluated instead of the causal Green's function.
2.3 Virtual sources and receivers
Generally, the focusing function and Green's function are not directly available. These functions can be obtained through the use of the Marchenko method (Broggini et al., 2012; Wapenaar et al., 2014; van der Neut et al., 2015), which is a data-driven method that requires only reflection data at the surface of the Earth and an estimation of the first arrival of the wave field at the location of interest inside the medium. The method handles the primaries of the reflection data in the same way as conventional methods; however, unlike those methods, the Marchenko method can also correctly handle the multiples in the data. The first arrival can be estimated through the use of a macro-velocity model. The method cannot handle attenuation on the reflection data and ignores evanescent waves. On field data, the data require additional processing to account for these and other requirements. The Marchenko method has been applied successfully on both synthetic and field data; for examples see Ravasi et al. (2016), Staring et al. (2018) and Brackenhoff et al. (2019).

Figure 3Schematic setup for (a) the two-step process and (b) the one-step process for retrieving the homogeneous Green's function in the subsurface. The red and green arrows show the focusing functions that are used to respectively create the virtual receiver and virtual source location. The red and green dots show the locations for the virtual receiver and virtual source, respectively. The black star indicates the source location of a real subsurface response, indicated with a black arrow, that is measured at the surface 𝕊0 on the same receiver location x as the focusing and Green's functions. is a surface located just above 𝕊0 on which the source locations x′ of the reflection response are located. The rays in this figure indicate full Green's functions and focusing functions, including multiple scattering.
The method can be used in the homogeneous Green's function retrieval scheme in two ways, which are schematically shown in Fig. 3. The first approach is a two-step process, as shown in Fig. 3a, where both the source and receiver of the homogeneous Green's function are obtained by redatuming them from the reflection response. This type of source–receiver redatuming is discussed in Sect. 3.4 of our companion paper by Wapenaar et al. (2019). First, we consider the fact that the data that we use in the field are band-limited and therefore a source signal s(t) is convolved with the Green's function, which changes its phase and amplitude:
where is a pressure wave field in the medium and s(ω) is the Fourier transform of the source signal. For the first step, we introduce a second surface that is located just above 𝕊0 and assume that a reflection response of the medium has been measured; x′ is the source location on the surface . The reflection response is used to create a virtual source location in the subsurface. To this end, we utilize a modification of Eq. (12) and use Eq. (13b) to create an equivalent version for pressure wave fields, which is the same as Eq. (41) of our companion paper:
In Eq. (14), we assume that the source spectrum is strictly real-valued. The focusing function is obtained through use of the Marchenko method and employed in Eq. (14) to create a wave field with a virtual source location, which is indicated by the green line in Fig. 3a. This function will be used to create a source location for the wave field retrieved through the homogeneous Green's function representation. This source is called a virtual source because it is not physically present in the subsurface.
In the second step of the process, using the Marchenko method, many focusing functions are created for focal points at varying locations in the medium that serve as the virtual receiver locations for the retrieved wave field. This is indicated by the red dots and arrows in Fig. 3a. Similarly to the virtual source, these are called virtual receivers because they are not physically present in the medium. We use these focusing functions in Eq. (10), which we modify using Eq. (13b) as follows:
In this representation, we make use of the wave field with the virtual source location that we obtained in the first step. The acausal part of the left-hand side of the time domain version of Eq. (14) can be removed easily by applying causality through the use of a Heaviside function. Since we assumed s(ω) to be real-valued, substitution of Eq. (15) into Eq. (7) yields
where . This is a similar representation to Eq. (39) for modified back propagation from our companion paper by Wapenaar et al. (2019).
The second way we can use the Marchenko method in the application of homogeneous Green's function retrieval is a one-step process during which the Marchenko method is only used to retrieve focusing functions to create virtual receivers. This is shown in Fig. 3b. Here, no virtual source is created from the reflection data using Eq. (14); rather, the actual response from a real source inside the medium is used, which is illustrated by the black star and arrow in Fig. 3b. The response that is monitored is used as in Eq. (15). It generally cannot be used in Eq. (16), however. If the source spectrum of the response is not strictly real-valued, the signal is not symmetric in time because , and therefore there will be a phase difference between the causal and acausal wave field, making the superposition of the signal with its time-reverse incorrect. Assuming that through processing of the signal, the type of wavelet that is applied to the data can be controlled, symmetry of the source signal can be ensured by using zero-phase wavelets. When this condition is fulfilled, Eq. (16) can be used for the subsurface response. Monitoring real source signals is the eventual goal of this approach, such as for the case of induced seismicity. The boon of this method is that aside from the measured signal, no information about the source of the data is required. There are limitations to this approach as well; the most pressing is that to evaluate the integral, the signal needs to be recorded on the same receiver array that was used to record the reflection data.
2.4 Modifications for realistic induced seismicity sources
2.4.1 Double-couple point sources
For the case of induced seismicity, the source signal can be more complex than just a single monopole point source. To include the mechanics for induced earthquakes more accurately, the double-couple source mechanism can be included in the representation. The double-couple source mechanism is accepted as representative for an earthquake response if the wavelength of the signal is at least of the same dimension as the size of the fault that originated the earthquake (Aki and Richards, 2002). It can be implemented through the use of a moment tensor, which is useful for the case of finite-difference modeling (Li et al., 2014). The response of a monopole source and double-couple source for a homogeneous medium is shown in Fig. 4, along with their radiation patterns in the center. While the monopole source response has a uniform amplitude along the wave front, the double-couple source response has a varying amplitude and polarity along the wave front due to the variation in the radiation pattern. Consequently, the orientation of the double-couple source affects the source signal, which is visible in Fig. 4b, while the orientation of the monopole source does not matter. Hence, the orientation of the fault is crucial to the characteristics of the double-couple source signal. To include this orientation in the representation, we introduce the operator , which acts on the wave field and creates the double-couple source orientation from the monopole source signature. This operator is defined as
where is a component of the vector containing the partial derivatives acting on the monopole signal originating from source location xB, which turns it into a double-couple source mechanism, is a component of the unit vector that orients one couple of the signal parallel to the fault plane and is a component of the vector that orients the other couple perpendicular to the fault plane. The operator can be applied to Eq. (15):
Assuming that the source signal is symmetric in time, the operator is also applied to Eq. (16):
In these two equations, the operator can be freely applied to both sides because the integral is not evaluated over the source locations. Consequently, if the wave field response used as a source for the homogeneous wave field has a double-couple signature, the homogeneous wave field will also have a double-couple signature. Note that the operator does not operate on the focusing functions, and hence we can use the monopole responses for these signals.
2.4.2 Double-couple sources along extended faults
In the case of induced seismicity, the fault or rupture plane that triggers the signal can be larger than the wavelength of the signal. In this case, the double-couple point source is no longer a valid approximation for the source of the signal. Studies of induced faults suggest that the signal develops over the fault during an extended period of time (Buijze et al., 2017). To approximate this type of source, a superposition of many point sources can be utilized. The total signal of the resulting superposition can be written as the superposition of the individual signals:
where the superscript k indicates the number of the source location that has the source spectrum s(k)(ω). The different source spectra include a linear phase term that determines the time at which the signal is triggered along the fault plane. P(xA,ω) can be created in two different ways, similarly as before.
First, we consider the two-step process in which both the source and receiver are virtual. In this case, every source location can be treated separately to retrieve the homogeneous wave field, and the superposition can be done after each signal has been retrieved through Eq. (19) and then shifted over t(k):
where H is the Heaviside step function and t(k) is the time at which the kth signal originates on the fault. The Heaviside in Eq. (21) selects the shifted causal signal from the shifted homogeneous (two-sided) signal before the superposition takes place, which is required to construct the correct signal. If the shifted homogeneous signals were used instead, the shifted acausal part of later signals would overlap the causal part of signals that originated earlier. Through the use of Eq. (21) the correct signal can be retrieved.
In the case that the source signal is measured rather than virtually created, the same approach cannot be taken. This signal is by definition measured after superposition; therefore, each point source cannot be evaluated separately. To represent this, Eq. (18) is adjusted to take the implicit superposition into account, according to
In this scenario, the sum is inside the integral and the entire signal is superposed before the focusing function is applied to it. This also results in a superposition of contributions of the focusing function between the virtual receiver location and the fault plane (i.e., the second term on the left-hand side). Substituting Eq. (22) into Eq. (7) will not lead to a cancellation of the focusing function on the left-hand side, as the wave field does not have a symmetric source signal due to the time differences between all the sources. As such, Eq. (22) is the endpoint and we will not obtain a homogeneous wave field, but rather a signal between the source and virtual receiver plus additional artifacts caused by the focusing function between the virtual receiver and the fault plane. Similar to the single source, each set of artifacts maps in between the shifted direct arrival of the wave field and its time reversal. Due to the different shift of each signal, the artifacts overlap the shifted causal and acausal parts of other signals and cannot be easily separated. However, because of the limited duration of the artifacts, the signal at later times will be free from these artifacts. Additionally, due to the nature of the characteristic function, the artifacts also vanish when the source location is outside the volume 𝕍A. In other words, if the virtual receiver location xA is above the shallowest source location, the correct signal can be retrieved for this virtual receiver.
3.1 Numerical results
3.1.1 Monopole and double-couple point sources
To demonstrate the different approaches to homogeneous Green's function retrieval, we apply the methods first on synthetic data. Figure 5a shows a density model and Fig. 5b shows the accompanying P-wave velocity model. The model contains an area of faulting in the center of the model, which is highlighted with a black dashed line. To create the required reflection data, the model is used in a finite-difference modeling code for wave field modeling (Thorbecke and Draganov, 2011). An example of an acoustic common-source record from the center of the model is shown in Fig. 5c. This type of common-source record and a smoothed version of the velocity model in Fig. 5b are the only input that we will use for our applications. To retrieve the required Green's functions and focusing functions with the Marchenko method, we model the first arrival from a point in the subsurface to the surface of the medium using the smooth velocity model and a homogeneous density model. This first arrival is then used to initiate the Marchenko method to retrieve focusing functions and a Green's function from the reflection response at the surface (i.e., from the common-source records). The scheme that we use is based on the Marchenko code created by Thorbecke et al. (2017). This is a code for an acoustic wave field Marchenko method, excluding free-surface multiples in the reflection data. Free-surface multiples could be included in the scheme as shown by Singh et al. (2015), but this is beyond the scope of the current paper.
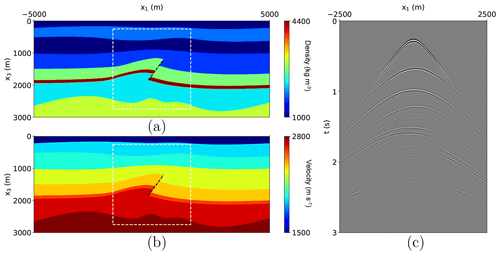
Figure 5(a) Density (kg m−3) and (b) P-wave velocity (m s−1) of the numerical model used to create reflection data. The white box denotes the area of interest for the purpose of homogeneous Green's function retrieval. The black dashed line indicates a fault plane. (c) Common-source record created using the model data in (a) and (b), with the source at the top center of the model, using a finite-difference modeling code and convolved with a 30 Hz Ricker wavelet.
Figure 6 shows the results of the homogeneous Green's function retrieval. All snapshots show the same area in the subsurface, which is denoted by the white box in Figs. 5a and b. Note that the box does not show the true aspect ratio of the area; however, the snapshots in Fig. 6 do. Each pixel in the image is a receiver location, and the source location for all images is exactly the same. The columns show snapshots of the wave field in the subsurface at four different points in time, 0, 150, 300 and 450 ms. Each row corresponds to a specific way the wave field in the subsurface was constructed. In the first row, the source and the receivers of the wave field are placed inside the model and the wave field is directly modeled. This is the benchmark that the other results will be compared to. All snapshots contain an overlay of black dashed lines, which indicate the locations of geological layer interfaces. As can be seen in the figure, the wave field of the modeling scatters at these lines.
The Marchenko-based approach is an improvement over classical methods as shown by Brackenhoff et al. (2019) because of the focusing functions that are utilized. To demonstrate this, we first consider a more conventional approach, namely the classical back propagation method from Sect. 2.4 of our companion paper by Wapenaar et al. (2019), from which we use Eq. (23):
where p− is the upgoing component of the pressure wave field at 𝕊0, and is the time-reversed first arrival of the Green's function and is the same first arrival that is used as the initial estimation of the focusing function used in the Marchenko method. For more information about the method, we refer the reader to our companion paper. Here, we demonstrate the issues with this approach, which can be seen in Fig. 6e–h. The primary upgoing wave field can be recovered using this method; however, the downgoing wave field is missing and strong artifacts are present. This is due to the fact that the multiples and the downgoing wave field are not taken into account properly using the back propagation method. To make a more detailed comparison between the result of this method and the modeling, we extract the measurements from two receiver locations. These locations are indicated in Fig. 6a, where the red dot is a receiver location above the source location and the blue dot a receiver location below the source location. Parts of these measurements are displayed in Fig. 7, where the left column corresponds to the red dot and the right column to the blue dot. The results in the rows of Fig. 7 correspond to the results of the rows in Fig. 6. However, the normalized amplitudes of the traces are used instead of the exact amplitudes. This is done because the first arrivals that were used for the Marchenko method and back propagation were retrieved in a smooth velocity medium without any density information, which is realistic, considering the availability of data in the field. Because of these limitations the absolute amplitude of the first arrival will be incorrect; while this has no effect on the relative amplitude, it does cause an incorrect overall scaling on the final retrieved wave field. However, we can still use the normalized traces to analyze the events that are retrieved with the correct relative amplitude. The trace in Fig. 7c, located above the virtual source, shows that while some of the correct events are retrieved, a large amount of desired events are missing. These problems are more severe for the receiver below the source location. In Fig. 7d, physical events are missing and there are artifacts present all over the trace. The classical back propagation method lacks a great deal of accuracy.
The third row of Fig. 6 shows the result of Green's function retrieval using the method described by Eq. (15). The Green's function and focusing functions that are required for this method are retrieved using the Marchenko method. This means that all the receivers and the source are virtual. When the result is compared to the benchmark, it is clear that there are some issues. The wave field below the source location, as indicated by the yellow dashed line, contains numerous artifacts, and the downgoing direct arrival of the wave field is missing; however, the coda of the wave field is present both above and below the source location, which is a significant improvement over the back propagation. The remaining errors below the source location are caused by the fact that the focusing function between the virtual source and receiver is present, and the lack of compensation for these contributions causes artifacts in the final result. When the virtual receivers are located above the virtual source location, the wave field is comparable to the benchmark and the direct arrival is present. When the trace in Fig. 7a is compared to e, the arrival times of the events match and there are no artifacts present; however, there is a mismatch in amplitude. This is due to transmission losses in the reflection response that the Marchenko method in its current form does not compensate for. These effects have been partially compensated for through the use of the method discussed by Brackenhoff (2016), although not all the effects have been removed. Also, we expect some numerical issues due to the fact that the modeling and the retrieval of the data are two fundamentally different approaches and the data are discretized. The modeling of the first arrival in the smooth model not only affects their amplitudes, but the arrival times will also shift slightly. Due to this slight shift the sampling points of the modeling and the retrieved wave field may not match exactly. We ensure that the wavelet is zero-phase for the modeling and the Marchenko method to fulfill the symmetric source signal requirement for the homogeneous Green's function representation. When the receiver location below the source is considered in Fig. 7f, the results are less accurate. The trace of the modeling contains no signal before the first arrival, whereas the trace for the Green's function retrieval contains numerous events and is lacking the first arrival. The coda of the traces shows a match that is comparable to the receiver location above the source. The arrival times of the events show a good match, while the amplitudes show errors. Because this receiver is located deeper inside the model, the transmission effects are stronger and therefore the error is larger.
Next, the homogeneous Green's function retrieval using Eq. (16) is considered. The input for this approach is exactly the same as the one used for the previous approach using Eq. (15); however, this time, we expect to retrieve the correct result. Looking at Fig. 6m–p, the result more closely matches the result of the benchmark. The improvement over the previous result for the deeper virtual receivers is clear. For some of the deeper receivers, part of the wave field is still not completely present, however. This is the part of the wave field that has a steep angle. The reason for this missing part is that the reflection response at the surface does not contain the reflections corresponding to the angles at larger depths, as they travel outside the aperture of the recording survey. Therefore, these steep angles cannot be reconstructed. As can be seen when the trace from Fig. 7e is compared to g, the result of the two approaches is exactly the same if the virtual receiver is located above the source. The improvement is noticeable when the receiver is located below the source. Figure 7h does contain the first arrival and lacks any signal before this arrival; it therefore shows a better match to Fig. 7b. While the amplitude mismatch is still present, the arrival times of the events match and no artifacts are present. This also shows that the coda of Fig. 7f is correctly retrieved. We have indicated the moment that the correct coda is retrieved with a yellow line in this figure.

Figure 6Snapshots of the wave field inside the white box in Fig. 5 for point sources. (a–d) Directly modeled wave field using the exact model from Fig. 5a and b. (e–h) Back-propagated wave field obtained using Eq. (23). (i–l) Wave field in the subsurface, retrieved for virtual receivers and a virtual source using Eq. (15). The yellow line indicates the border between the area below and above the virtual source. (m–p) Similar to (i–l) for the homogeneous wave field using Eq. (16). (q–t) Similar to (m–p) using Eq. (19) and a double-couple signature inclined at an angle of 45∘. All wave fields have been convolved with a 30 Hz Ricker wavelet. The red and blue dot indicate the locations of the traces in Fig. 7. The black dashed lines indicate the locations of geological layer interfaces.
To make a more careful comparison between the modeled wave field and the wave fields retrieved from the reflection data, we plotted the traces from Fig. 7a–h together in Fig. 8, where the left column shows the result for the traces above and the right column shows the result for the traces below the virtual source location. Each subplot contains the modeled response with an overlay of one of the retrieval methods. The back propagation method shows very large errors for both receiver locations as can be seen in Fig. 8a and b. Strong physical events are missing and artifacts are present on both traces. When comparing the results in Fig. 8c, the match of the events between the modeled wave field and the retrieved wave field is not perfect. As mentioned before, this is due to the influence of the smooth model and numerical effects that occur. A similar match can be seen in Fig. 8e. The retrieval of the Green's function with the artifacts below the source location, which is displayed in Fig. 8d, shows the errors at an early time; however, it also demonstrates that the events in the coda are well captured. This error is not present in the case of the homogeneous Green's function retrieval as shown in Fig. 8f. These results show that the approach using the Marchenko method is capable of retrieving the relative amplitudes of the events and can retrieve arrival times that are very close to the actual arrival times, even if a smooth velocity model is used.
Finally, we consider the situation in which the source mechanism is more complex through the use of a double-couple signature. The retrieval in this case corresponds to the approach in Eq. (19) using a virtual source. The double-couple is an elastic mechanism; however, as we only require the first arrival to initiate the Marchenko method, the coda of the wave field is not of interest. The S-wave velocity used for the modeling of the first arrival is set to 500 m s−1 to ensure that all the S-wave events arrive after the first P-wave arrival. We incline the double-couple source at an angle of 45∘ and use it to model the first arrival, which is used to initiate the Marchenko method to retrieve the wave field response for the virtual source location. The focusing functions remain the same as the ones we used for the previous approaches in Fig. 6e–h. The result of this retrieval is shown in Fig. 6q–t. As Eq. (19) states, because the Green's function contains a double-couple signature, the homogeneous Green's function contains the same signature in both the direct arrival and in the coda of the wave field. The double-couple signature affects the amplitude of the wave field depending on the angle of the wave front; however, the arrival times are similar to those when a monopole virtual source is used. This becomes clear when the traces from Fig. 7i–j are considered. The arrival times for the events are similar to the previous result; however, there are apparent amplitude and phase differences caused by the different types of source signatures. Due to these differences, we have not included these traces in Fig. 8, as a direct comparison between the events cannot be made. The result shows that the double-couple signature can be successfully integrated in the Marchenko method.
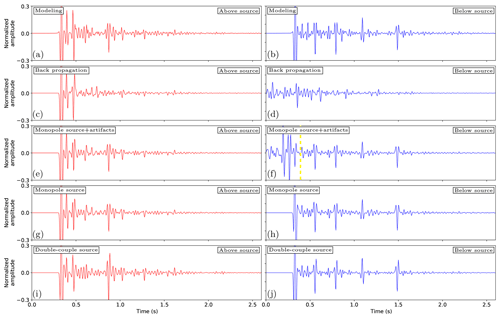
Figure 7Traces from receivers in the subsurface at two locations, extracted from Fig. 6. In the left column, the receiver is located above the source and corresponds to the red dot in Fig. 6a, and in the right column it is located below the source and corresponds to the blue dot in Fig. 6a. (a–b) Directly modeled wave field using the exact model from Fig. 5a and b. (c–d) Back-propagated wave field obtained using Eq. (23). (e–f) Wave field in the subsurface, retrieved for virtual receivers and a virtual source using Eq. (15). The yellow line in (f) indicates the time after which the correct signal is retrieved. (g–h) Similar to (e–f) for the homogeneous wave field using Eq. (16). (i–j) Similar to (g–h) using Eq. (19) and a double-couple signature inclined at an angle of 45∘. All wave fields have been convolved with a 30 Hz Ricker wavelet.
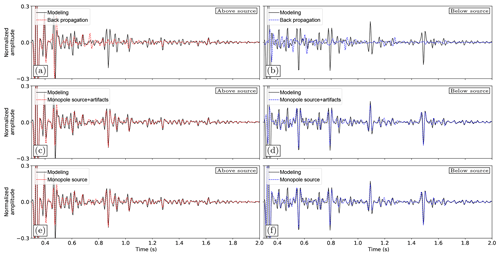
Figure 8(a) Overlay of the traces from Fig. 7a and c. (b) Similar to (a) for the traces from Fig. 7b and d. (c) Similar to (a) for the traces from Fig. 7a and e. (d) Similar to (a) for the traces from Fig. 7b and f. (e) Similar to (a) for the traces from Fig. 7a and g. (f) Similar to (a) for the traces from Fig. 7b and h. All wave fields have been convolved with a 30 Hz Ricker wavelet.
3.1.2 Double-couple sources along extended faults
Until now, we have only considered single point sources that have a symmetric signal. To study the situation of induced seismicity, we simulate a source that evolves over time over a larger area than a single point. We achieve this by placing a collection of sources along a line in the model. For this purpose, we place 131 sources along the fault plane that was indicated in Fig. 5, starting at the bottom left corner, with a spacing of 7.07 m. The time between the activation of the shots is 12 ms, simulating a propagation speed of the source along the fault of 589 m s−1. The fault is inclined at 45∘, and therefore we make use of double-couple sources that are inclined at the same angle. We consider two scenarios, one in which we have virtual sources and one in which we have a measurement of a real source.
For the first scenario, we approach the problem by considering each source position individually. We do this by retrieving the homogeneous wave field for each virtual source location separately and by shifting and superposing the results, similar to Eq. (21). Causality is applied to each individual wave field before the superposition to avoid overlap between the causal and acausal part of the wave fields. Snapshots of the results are shown in Fig. 9a–d for 0, 500, 1000 and 1500 ms. The reason for the large time steps is to ensure that all the sources along the fault have been activated during the final snapshot. The propagation of the source location along the fault is clear in these snapshots; however, a propagating wave field appears to be largely absent, with only a few events and ringing effects present. The reason for this phenomenon is that the velocity at which the sources are activated along the faults is lower than the propagation velocity of the medium. This effectively means that the phase velocity of the combined wave field along the fault is lower than the propagation velocity of the medium, and the emitted wave field therefore becomes evanescent. This effect can be seen more clearly by considering the traces from two receiver positions. Similar to Fig. 7, we extract the same receiver locations to consider the individual traces, as shown in Fig. 10. In Fig. 10a–b, the trace for the receiver location above the shallowest source location shows a trace with few events, except for some high-amplitude events. The receiver location below the deepest source shows a trace that contains more ringing effects with a uniform amplitude. Because the amplitudes are similar and the events located close together, little information can be gained from this trace.
In reality, faults are not uniform; rather, they are strongly heterogeneous, which causes variations for the source amplitude along the fault plane. To account for this effect, we apply random scaling to each source location along the fault plane before the superposition takes place. Applying a random scaling factor to the wave field only affects the amplitudes of the wave fields and does not affect the arrival times or the presence of the events in the wave field. The result of this approach is shown in Fig. 9e–h. The propagation of the source location along the fault is similar to the uniform-amplitude approach; however, the individual wave fields are visible due to the random-amplitude approach. Both the first arrivals and the codas can be seen, although there is much overlap between all the wave fields, which makes distinguishing individual events at later times challenging. When the two receiver traces in Fig. 10c–d are studied, this challenge is still present. The trace contains events; however, it is difficult to say whether these events correspond to the response of one source or another.
To make an estimation for the arrival times of the retrieved response, we numerically model the line source in the subsurface using the same random amplitude distribution as in the previous case. As we lack the capability to model snapshots of the response to the double-couple source acoustically, we make use of monopole point sources instead of double-couple sources. As a result, the amplitudes of the events should not be compared to the retrieved response; however, the arrival times can be compared. The wave field in Fig. 9i–l shows that the arrival times are comparable between the modeling result and the retrieved response. This is further proven when the traces in Fig. 10e–f are considered. The arrival times have a strong match, while the amplitudes are not comparable. This confirms that the correct events are retrieved through this approach.

Figure 9Snapshots of the wave field inside the white box in Fig. 5 for line sources. (a–d) Response in the subsurface, retrieved using Eq. (21) for virtual receivers and virtual double-couple sources inclined at 45∘ with a uniform amplitude. (e–h) Similar to (a–d) using random amplitudes for the source. (i–l) Directly modeled wave field using the exact model from Fig. 5a and b and monopole point sources with a random amplitude. (m–p) Similar to (e–h) using a superposition of double-couple sources with random amplitudes using Eq. (22). The yellow line indicates the border between the area below and above the shallowest source. (q–t) Similar to (e–h), but instead of using the homogeneous Green's function retrieval, the back propagation using Eq. (23) is used for each source position. (u–x) Similar to (m–p), but instead of using the Green's function retrieval, the back propagation using Eq. (23) is used. All wave fields have been convolved with a 30 Hz Ricker wavelet. The red and blue dot indicate the locations of the traces in Fig. 10. The black dashed lines indicate the locations of geological layer contrasts.
Next, we consider a different scenario with a real source instead of a virtual one. Here, we once again retrieve the wave field response of each source separately. However, instead of retrieving a separate wave field for each of these responses and then superposing these results together, we superpose the responses before the wave field is retrieved, following Eq. (22). By using this approach we obtain a response record that matches the response of a real source recording in the subsurface. The same random amplitude distribution that we used for the previous two results is applied for this approach as well to make the comparison fair. The wave field that is obtained is shown in Fig. 9m–p, where we can see that the propagation of the source location along the fault is captured properly. There are issues with the approach due to the limitation of the representation that is used. The response to each source has artifacts that arrive before the first arrival when the virtual receiver is located below any of the source locations. These effects overlap the causal wave fields of sources at other locations and obscure the events that should be present. Additionally, the downgoing first arrival is missing for all source locations. These problems are inherent to the representation and cannot be easily avoided; however, the coda of the response for later times will be correct, as we saw for the point source in Fig. 7e–h. When the traces for this approach from Fig. 10g–h are studied, we can see that if the receiver is located below the source locations, individual events belonging to the sources are impossible to distinguish. If the receiver is located above all the sources, however, the response is retrieved correctly. The lower receiver contains the correct coda at a later time. We indicated this moment with a yellow line in Fig. 10h, similar to Fig. 7f. This, combined with the fact that the source location of the signal can be clearly distinguished, shows that this approach has potential for field recordings.
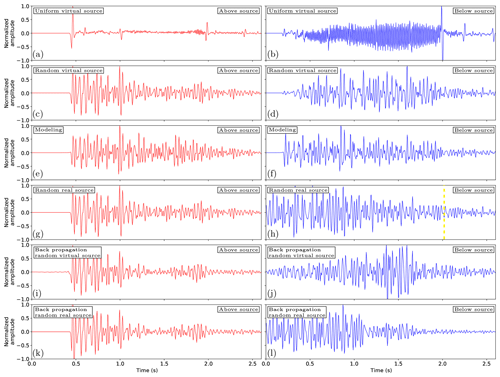
Figure 10Traces of receivers in the subsurface at two locations, extracted from Fig. 9. In the left column, the receiver is located above the source and corresponds to the red dot in Fig. 9a, and in the right column it is located below the source and corresponds to the blue dot in Fig. 9a. (a–b) Response in the subsurface, retrieved using Eq. (21) for virtual receivers and virtual double-couple sources inclined at 45∘ with a uniform amplitude. (c–d) Similar to (a–b) using random amplitudes for the source. (e–f) Directly modeled wave field using the exact model from Fig. 5a and b and monopole point sources with a random amplitude. (g–h) Similar to (c–d) using a superposition of double-couple sources with random amplitudes using Eq. (22). The yellow line in (h) indicates the time after which the correct signal is retrieved. (i–j) Similar to (c–d), but instead of using the homogeneous Green's function retrieval, the back propagation using Eq. (23) is used for each source position. (k–l) Similar to (g–h), but instead of using the Green's function retrieval, the back propagation using Eq. (23) is used. All wave fields have been convolved with a 30 Hz Ricker wavelet.
Finally, as an example for the improvement of this approach over conventional methods, we repeat the retrieval of a fault plane source using the back propagation method. We consider both the approach for retrieving a virtual source and retrieving a real source. For the first approach, we retrieve the response for each source location, mute the acausal part of the response and shift it in time to create one source signal. However, instead of using homogeneous Green's function retrieval to obtain the responses, we employ the classic back propagation and show the resulting wave field in Fig. 9q–t. While the primary upgoing wave field is still captured, the coda and the downgoing wave field are absent. Aside from the missing events, artifacts are present at all times in the result. When the extracted traces are considered in Fig. 10i–j, we can see that the trace is completely different to the traces in Fig. 10c–d. Due to the fact that the missing events and the artifacts shift along with the source position, it masks the entire trace.
The effects of the classical back propagation approach have a similar result when we repeat the experiment for our real source example. We use classical back propagation instead of Green's function retrieval on the simulated real source response and show the result in Fig. 9u–x. Similar problems with the coda and the downgoing wave field are present, and the artifacts in the wave field still occur. The extracted trace above the source locations in Fig. 10k shows the same result as in Fig. 10i, which is consistent with the previous results. The extracted trace below the source locations in Fig. 10l shows the strong degradation in quality and has no match with the desired result in Fig. 10d. This shows that for both types of sources, real or virtual, the single-sided approach with a focusing function is an improvement over the classical approach using back propagation. Therefore, the latter approach will not be used for the field data.
3.2 Field data results
To demonstrate that our approach is not limited to synthetic data, we also apply the method on field reflection data. The field data were recorded in the Vøring basin in a marine setting by SAGA Petroleum A.S., which is currently part of Equinor. Due to the setting, the receivers only recorded P waves. The data consist of 399 common-source records, an example of which is shown in Fig. 11c. The data were preprocessed before the application of the homogeneous Green's function retrieval through the use of the estimation of primaries through sparse inversion (EPSI) method to remove the source wavelet, retrieve the near offsets and remove the free-surface multiples (van Groenestijn and Verschuur, 2009). Moreover, we applied source–receiver reciprocity to allow for the retrieval of two directions of offset and adaptive corrections to compensate for attenuation and incorrect source strength. Along with the reflection data, a smooth P-wave velocity model was also provided, which is shown in Fig. 11a. We indicate the region of interest, where we will perform homogeneous Green's function retrieval, with a white dashed box. The model is not displayed in a true-to-life aspect ratio. The reflection data and the velocity model are the only inputs that are available for the homogeneous Green's function retrieval. No direct information about the subsurface is available for this area; however, using the reflection data and the velocity model, an image of the subsurface was created using the Marchenko method, shown in Fig. 11b, which we will use as a reference point at which scattering is expected to take place. This imaging was done independently of the homogeneous Green's function retrieval and is only used as a reference. More information about imaging using the Marchenko method, as well as an application on field data, can be found in Staring et al. (2018). The homogeneous Green's function retrieval for this dataset has been successfully performed, as was shown in Brackenhoff et al. (2019); however, in this work we will expand the results to include the line source configuration.
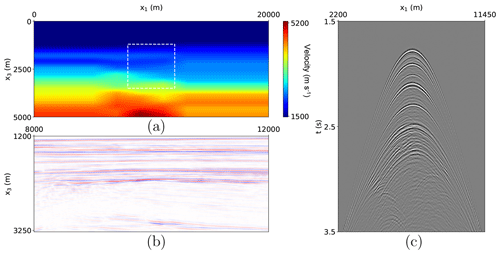
Figure 11Real data example, with the (a) P-wave velocity (m s−1) of the field data. The white box denotes the area of interest for the purpose of homogeneous Green's function retrieval. (b) Image of the subsurface located in the region indicated by the white dashed box. (c) Common-source record of the field reflection data, processed for the purpose of applying the Marchenko method. The reflection data source wavelet was reshaped to a 30 Hz Ricker wavelet. The data were recorded in the Vøring basin in Norway and provided by Equinor.
Because there is no information about the subsurface available, we cannot directly model in the subsurface and therefore have no benchmark; however, we have shown with the previous examples that the method is capable of retrieving the correct result. We perform homogeneous Green's function retrieval in the subsurface for both a virtual source and virtual receivers. The virtual source is a double-couple source inclined at −20∘. The result is shown in Fig. 12a–d for 0, 300, 600 and 900 ms. The image of the subsurface from Fig. 11b is used as an overlay to help indicate the region where scattering of the wave field is expected. The scattering takes place along regions where high amplitudes are present for the subsurface image, which indicates a match between the image and the homogeneous wave field. Aside from the direct arrival, there is also a coda present, which contains several events. The result is not as clean as the synthetic data, however. This is due to the limitations of the field data. The data are attenuated, a problem that the Marchenko method cannot properly account for. The attenuation has been corrected for during the processing; however, this process is imperfect and will leave imperfections in the final result. There is also incoherent noise present in the field data, which has not been removed during the processing and will be present in the final result.
Figure 12a shows a red and blue dot, which indicate the location of traces that are extracted and are shown in the left and right column of Fig. 13, respectively. No benchmark for these traces is available, and thus it cannot be directly validated. The results in Fig. 13a–b show that the traces contain multiple well-defined events and that the noise on the trace has lower amplitudes than these events. The amplitude of the first arrival is strong compared to the coda and the phase of all the events is similar. This shows that if the faults in the model are small compared to the wavelength, this approach can be useful for interpretation and characterization of the source mechanism.

Figure 12Snapshots of the wave field inside the white box in Fig. 11 for the field data. (a–d) Homogeneous wave field in the subsurface, retrieved for virtual receivers and a virtual double-couple source inclined at −20∘ using Eq. (19). (e–h) Similar to (a–d) for a line source of double-couple sources with random amplitudes inclined at −22.4∘ using Eq. (21). (i–l) Similar to (e–h) using a superposition of double-couple sources with random amplitudes using Eq. (22). The yellow line indicates the border between the area below and above the shallowest source. The images are overlain with the image of the subsurface from Fig. 11b. All wave fields had their source wavelets reshaped to a 30 Hz Ricker wavelet.
Next, we consider the two line source configurations for the virtual and the real source configuration. As there is no clear fault present in the model, the fault line is arbitrarily placed in the center of the model, inclined at an angle of −22.4∘; 161 sources are used with a spacing of 6.99 m, whereby the time between the activation of the shots is 12 ms, simulating a propagation speed of the source along the fault of 583 m s−1. A random amplitude is assigned to each of the source locations to generate propagating waves. The first situation we consider is using Eq. (21), whereby homogeneous Green's function retrieval is performed for each location separately, the results are superposed and causality is imposed. The results of this approach are shown in Fig. 12e–h for 0, 1000, 2000 and 3000 ms. Similar to the synthetic data, the movement of the source is well captured and the first arrival and the coda are present in the signal. Part of the wave field is not present; this corresponds to high angles at deeper depths, which, as we explained before, are not present in the reflection response and therefore cannot be reconstructed. The result has a similar quality as the single double-couple source in Fig. 12a–d and the results on the synthetic data Fig. 9.
There is no induced seismicity signal present for this area, so a real source signal cannot be used, but we simulate this as follows. Similar to the approach for the synthetic data, we use the Marchenko method to retrieve a wave field response with a double-couple signature for each source location. These signals are then superposed to create a single source record as a substitute for a real source signal. This approach follows Eq. (22), the results of which are shown in Fig. 12i–l. Similar to the results for the synthetic data, the match between the two approaches above the shallowest source location is strong. This is proven further when the traces above the source from Fig. 13c and e are compared to each other. The traces are nearly identical. If we consider a location below the deepest source location, the results are less comparable, again similar to the results that were achieved on the synthetic data. The traces for this location, shown in Fig. 13d and f, support this conclusion. The match in this situation is nonexistent for earlier times, and the information is hard to appraise. At later times, as indicated by the yellow line, the coda of the two approaches match each other, similar to what was seen before. For both types of retrieval, the source locations are well defined in both time and space and not obscured by artifacts that could cast doubt on the source locations. Using both types of approach shows potential for the determination of the source location and the coda and can help in the characterization of the fault mechanism.
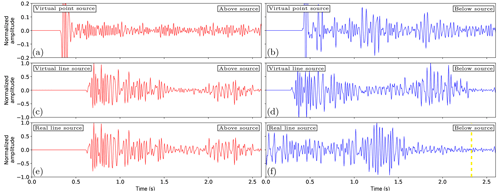
Figure 13Traces of receivers in the subsurface at two locations, extracted from Fig. 12. In the left column, the receiver is located above the source and corresponds to the red dot in Fig. 12a, and in the right column it is located below the source and corresponds to the blue dot in Fig. 12a. (a–b) Homogeneous wave field in the subsurface, retrieved for virtual receivers and a virtual double-couple source inclined at −20∘ using Eq. (19). (c–d) Similar to (a–b) for a line source of double-couple sources with random amplitudes inclined at −22.4∘ using Eq. (21). (e–f) Similar to (c–d) using a superposition of double-couple sources with random amplitudes using Eq. (22). The yellow line in (f) indicates the time after which the correct signal is retrieved. All wave fields had their source wavelets reshaped to a 30 Hz Ricker wavelet.
In this paper, we considered two methods to monitor full wave fields in the subsurface using the Marchenko method and found that in both cases, the Marchenko-based approach is an improvement over classical methods such as back propagation. The first method is based on the creation of both virtual receivers and virtual sources in the subsurface. In this case, all the signals are created from the reflection data at the surface, and no response from a real subsurface source is used. For virtual point sources, we showed that we can ensure that the source signal is symmetric and that therefore the full homogeneous wave field can be retrieved without artifacts. The main limitation is that the steepest part of the wave field at large depths cannot be retrieved. This approach works for virtual sources with both a monopole signature and a more complex double-couple signature, the latter of which was used as a model for a small-scale induced seismicity signal. Larger-scale induced seismicity signals emitted from a fault plane were considered as well, simulated by a series of individual point sources with a double-couple signature. For this case, the homogeneous wave field was retrieved for all the sources separately, after which the causal parts were isolated, shifted in time and superposed together. This produces a response from an extended fault rupture that is operating over a larger window of time, which produces a far more complex signal. All the source locations can be distinguished using this method. This method can be used to forecast in a data-driven way the response to possible future induced seismic events.
The second method we considered creates virtual receivers in the subsurface that observe a real response from a subsurface source. To this end, we considered point sources for which the source signal was not assumed to be symmetric in time. The causal wave field that is retrieved in this case is missing a part of the direct arrival and contains artifacts. These problems are only present when the virtual receiver is located below the source location, and the artifacts map exclusively in the time interval between the direct arrival of the wave field and its time reversal. The coda of the causal wave field is retrieved in full, as is the source location of the subsurface response. When considering the responses propagating from a fault, the artifacts are more severe. Unlike in the method with the virtual sources, to simulate the response to a real rupturing fault, we shifted and superposed the source responses before the Green's function retrieval. Because of this, the artifacts are present for each point source; however, due to the time shift, the artifacts of one response coincided with the causal coda of other responses. As a result the coda of the retrieved wave field is only partially obtained. The source locations of the fault response are retrieved correctly. This method can be used to monitor in a data-driven way the response to actual induced seismic events everywhere between the surface and the source.
We applied the two methods to synthetic and field data. For the synthetic data we showed that the retrieved responses match very well with directly modeled responses. The results obtained from the field data are very similar to those obtained from the synthetic data. The results on the datasets show the potential for the application of the method on real source signals in the future.
The modeling and processing software that have been used to generate the numerical examples in this paper can be downloaded from https://github.com/JanThorbecke/OpenSource (Thorbecke et al., 2014).
The seismic reflection data analyzed in Figs. 11, 12 and 13 are available from Equinor ASA, but restrictions apply to the availability of these data, which were used under license for the current study and are therefore not publicly available. Data are, however, available from the authors upon reasonable request and with the permission of Equinor ASA.
The supplement related to this article is available online at: https://doi.org/10.5194/se-10-1301-2019-supplement.
The videos of the snapshots in Figs. 6, 9 and 12 can be found at https://github.com/JanThorbecke/OpenSource/tree/master/movies (last access: 29 July 2019).
JB wrote the paper. KW and JB devised the methodology. JB and JT developed the software and generated the numerical examples. All authors reviewed the paper.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Advances in seismic imaging across the scales”. It is a result of the EGU General Assembly 2018, Vienna, Austria, 8–13 April 2018.
The authors thank Equinor ASA for giving us permission to use the vintage seismic reflection data of the Vøring Basin and Eric Verschuur and Jan-Willem Vrolijk for their assistance with the processing of the vintage seismic reflection data. The authors thank Matteo Ravasi, Dominic Cummings and an anonymous reviewer for their review and suggestions to improve this paper.
This work has received funding from the European Union’s Horizon 2020 research and innovation program: European Research Council (grant agreement no. 742703).
This paper was edited by Nicholas Rawlinson and reviewed by Matteo Ravasi, Dominic Cummings, and one anonymous referee.
Aki, K. and Richards, P. G.: Quantitative seismology, University Science Books, 2002. a
Brackenhoff, J.: Rescaling of incorrect source strength using Marchenko redatuming, M.sc. thesis, Delft University of Technology, Delft, Zuid-Holland, the Netherlands, available at: http://resolver.tudelft.nl/uuid:0f0ce3d0-088f-4306-b884-12054c39d5da (last access: 29 July 2019), 2016. a
Brackenhoff, J., Thorbecke, J., and Wapenaar, K.: Virtual sources and receivers in the real Earth, a method for induced seismicity monitoring, arXiv preprint, arXiv:1901.03566, 2019. a, b, c, d
Broggini, F., Snieder, R., and Wapenaar, K.: Focusing the wavefield inside an unknown 1D medium: Beyond seismic interferometry, Geophysics, 77, 25–28, 2012. a
Buijze, L., van den Bogert, P. A., Wassing, B. B., Orlic, B., and ten Veen, J.: Fault reactivation mechanisms and dynamic rupture modelling of depletion-induced seismic events in a Rotliegend gas reservoir, Neth. J. Geosci., 96, 131–148, 2017. a
Curtis, A., Nicolson, H., Halliday, D., Trampert, J., and Baptie, B.: Virtual seismometers in the subsurface of the Earth from seismic interferometry, Nat. Geosci., 2, 700–704, https://doi.org/10.1038/ngeo615, 2009. a
Eisner, L., Hulsey, B., Duncan, P., Jurick, D., Werner, H., and Keller, W.: Comparison of surface and borehole locations of induced seismicity, Geophys. Prospect., 58, 809–820, 2010. a
Hatchell, P. and Bourne, S.: Rocks under strain: Strain-induced time-lapse time shifts are observed for depleting reservoirs, The Leading Edge, 24, 1222–1225, 2005. a
Herwanger, J. V. and Horne, S. A.: Linking reservoir geomechanics and time-lapse seismics: Predicting anisotropic velocity changes and seismic attributes, Geophysics, 74, 13–33, 2009. a
Li, D., Helmberger, D., Clayton, R. W., and Sun, D.: Global synthetic seismograms using a 2-D finite-difference method, Geophys. J. Int., 197, 1166–1183, 2014. a
Magnani, M. B., Blanpied, M. L., DeShon, H. R., and Hornbach, M. J.: Discriminating between natural versus induced seismicity from long-term deformation history of intraplate faults, Sci. Adv., 3, e1701593, https://doi.org/10.1126/sciadv.1701593, 2017. a
McClellan, J. H., Eisner, L., Liu, E., Iqbal, N., Al-Shuhail, A. A., and Kaka, S. I.: Array processing in microseismic monitoring: Detection, enhancement, and localization of induced seismicity, IEEE Signal Proc. Mag., 35, 99–111, 2018. a
Oristaglio, M. L.: An inverse scattering formula that uses all the data, Inverse Probl., 5, 1097–1105, 1989. a, b
Porter, R. P.: Diffraction-limited, scalar image formation with holograms of arbitrary shape, J. Opt. Soci. Am., 60, 1051–1059, 1970. a, b
Porter, R. P. and Devaney, A. J.: Holography and the inverse source problem, J. Opt. Soc. Am., 72, 327–330, 1982. a, b
Ravasi, M., Vasconcelos, I., Kritski, A., Curtis, A., da Costa Filho, C. A., and Meles, G. A.: Target-oriented Marchenko imaging of a North Sea field, Geophys. J. Int., 205, 99–104, 2016. a
Singh, S., Snieder, R., Behura, J., van der Neut, J., Wapenaar, K., and Slob, E.: Marchenko imaging: Imaging with primaries, internal multiples, and free-surface multiples, Geophysics, 80, 165–174, 2015. a
Slob, E., Wapenaar, K., Broggini, F., and Snieder, R.: Seismic reflector imaging using internal multiples with Marchenko-type equations, Geophysics, 79, 63–76, 2014. a
Staring, M., Pereira, R., Douma, H., van der Neut, J., and Wapenaar, K.: Source-receiver Marchenko redatuming on field data using an adaptive double-focusing method, Geophysics, 83, 579–590, 2018. a, b
Thorbecke, J. and Draganov, D.: Finite-difference modeling experiments for seismic interferometry, Geophysics, 76, 1–18, 2011. a
Thorbecke, J., Brackenhoff, J., and Holicki, M.: OpenSource, Github, available at: https://github.com/JanThorbecke/OpenSource (last access: 29 July 2019), 2014.
Thorbecke, J., Slob, E., Brackenhoff, J., van der Neut, J., and Wapenaar, K.: Implementation of the Marchenko method, Geophysics, 82, 29–45, 2017. a
van der Neut, J., Vasconcelos, I., and Wapenaar, K.: On Green's function retrieval by iterative substitution of the coupled Marchenko equations, Geophys. J. Int., 203, 792–813, 2015. a, b
van Groenestijn, G. and Verschuur, D.: Estimation of primaries and near-offset reconstruction by sparse inversion: Marine data applications, Geophysics, 74, 119–128, 2009. a
van Thienen-Visser, K. and Breunese, J.: Induced seismicity of the Groningen gas field: History and recent developments, The Leading Edge, 34, 664–671, 2015. a
Wapenaar, K., Fokkema, J., and Snieder, R.: Retrieving the Green’s function in an open system by cross correlation: A comparison of approaches (L), J. Acoust. Soc. Am., 118, 2783–2786, 2005. a
Wapenaar, K., Thorbecke, J., van Der Neut, J., Broggini, F., Slob, E., and Snieder, R.: Marchenko imaging, Geophysics, 79, 39–57, 2014. a, b, c
Wapenaar, K., Thorbecke, J., and van der Neut, J.: A single-sided homogeneous Green's function representation for holographic imaging, inverse scattering, time-reversal acoustics and interferometric Green's function retrieval, Geophys. J. Int., 205, 531–535, 2016. a, b
Wapenaar, K., Brackenhoff, J., and Thorbecke, J.: Green's theorem in seismic imaging across the scales, Solid Earth, 10, 517–536, https://doi.org/10.5194/se-10-517-2019, 2019. a, b, c, d
Zhang, H. and Eaton, D. W.: Induced Seismicity Near Fox Creek, Alberta: Interpretation of Source Mechanisms, in: Unconventional Resources Technology Conference, Houston, Texas, 23–25 July, 2577–2584, Society of Exploration Geophysicists, American Association of Petroleum Geologists, Society of Petroleum Engineers, 2018. a