the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Integration of geoscientific uncertainty into geophysical inversion by means of local gradient regularization
Mark Lindsay
Vitaliy Ogarko
Mark Jessell
Roland Martin
Evren Pakyuz-Charrier
We introduce a workflow integrating geological modelling uncertainty information to constrain gravity inversions. We test and apply this approach to the Yerrida Basin (Western Australia), where we focus on prospective greenstone belts beneath sedimentary cover. Geological uncertainty information is extracted from the results of a probabilistic geological modelling process using geological field data and their inferred accuracy as inputs. The uncertainty information is utilized to locally adjust the weights of a minimum-structure gradient-based regularization function constraining geophysical inversion. Our results demonstrate that this technique allows geophysical inversion to update the model preferentially in geologically less certain areas. It also indicates that inverted models are consistent with both the probabilistic geological model and geophysical data of the area, reducing interpretation uncertainty. The interpretation of inverted models reveals that the recovered greenstone belts may be shallower and thinner than previously thought.
- Article
(12970 KB) - Full-text XML
- BibTeX
- EndNote
The integrated interpretation of multiple data types and disciplines in geophysical exploration is a powerful approach to mitigating the limitations inherent to each of the datasets. For instance, gravity data, which have poor horizontal resolution, can be integrated with seismic inversion to mitigate the poor lateral resolution of seismic inversion (Lelièvre et al., 2012). Likewise, geological modelling and geophysical inversions are routinely performed in the same area to obtain a subsurface model consistent with geological and geophysical measurements (Guillen et al., 2008; Lelièvre and Farquharson, 2016; Pears et al., 2017; Williams, 2008). When sufficient prior information is available, petrophysical constraints can be used in inversion (Lelièvre et al., 2012; Paasche and Tronicke, 2007) and integrated with geological modelling to derive local constraints (Giraud et al., 2017). However, in exploration scenarios, this can be impractical as the available petrophysical information may be insufficient to allow us to derive such constraints (Dentith and Mudge, 2014). In such cases, when more than one geophysical dataset is available, practitioners have relied on joint inversion using structural constraints (e.g. Gallardo and Meju, 2003; Haber and Oldenburg, 1997; Zhdanov et al., 2012). Alternatively, when one of the datasets has a spatial resolution that is superior to the others, structural information can be transferred into the gradient regularization constraint for the inversion of the lesser resolving method(s), thus mitigating some of the challenges faced by joint inversion in such cases, in what has been called “guided inversion” (Brown et al., 2012). This strategy has been applied in recent years using the interpretation of predominantly propagative data (e.g. seismics, ground-penetrating radar) to constrain the inversion of diffusive data (e.g. diffusive electromagnetic methods), as reported by Yan et al. (2017) and references reported therein. However, this avenue remains relatively underexplored to date.
In this article, we broaden the applications of guided inversion and explore the integration of non-geophysical information in inversion, such as geological uncertainty, into what we call uncertainty-guided inversion, where we focus on the complementarity of information content between the datasets. We introduce a new technique that integrates local uncertainty information derived from probabilistic geological modelling in the inversion of potential field data, following recommendations of Jessell et al. (2010, 2014, 2018), Lindsay et al. (2013a, 2014) and Wellmann et al. (2014, 2017). In contrast to Giraud et al. (2016, 2017), who derive local petrophysical constraints from petrophysical measurements and geological modelling results, constraints used in uncertainty-guided inversion are based solely on the local conditioning of a gradient regularization function, thereby offering the possibility to integrate probabilistic geological modelling into geophysical inversion in the absence of sufficient petrophysical information. Such conditioning relies on the calculation of local weights derived from prior geological information. In this study, we utilize a probabilistic geological model (PGM) (Pakyuz-Charrier et al., 2018b) consisting of the observation probability of the different lithologies of the area in every model cell. More specifically, we utilize the information entropy (Shannon, 1948; Wellmann and Regenauer-Lieb, 2012), which measures geological uncertainty in probabilistic models. We calculate it in each model cell of the PGM to derive spatially varying weights applied to the gradient regularization function used during inversion.
The integration methodology we develop is similar in philosophy to the work of Brown et al. (2012), Guo et al. (2017) and Wiik et al. (2015), who extract continuous structural information from seismic data to adjust the strength of the regularization term locally in order to promote specific structural features during electromagnetic inversion. However, our work differs from these authors in four main respects. Firstly, the geophysical problem we tackle is different in nature as we constrain potential field data in a hard-rock scenario instead of electromagnetic data in soft-rock studies. Secondly, we use a metric encapsulating geological uncertainty derived from geological measurements, whereas, in contrast, previous studies used other geophysical attributes. Thirdly, we allow inversion to update the model preferably in the most uncertain parts of the geological model, instead of encouraging a certain degree of structural similarity between two geophysical inverse models. Finally, while some of the previous work involves mostly 2-D models, every step of our modelling is performed purely in 3-D.
In this paper, we introduce the methodology and field application as follows. In the methodology section, we first introduce the inversion and integration scheme, and provide essential background information about probabilistic geological modelling. We then provide the essential background about information entropy before detailing its usage in inversion. In the ensuing section, we investigate the applicability of the proposed technique using a realistic synthetic case study. Following this, we present a field application case focused on the Yerrida Basin (Western Australia), starting with the introduction of the geological context and modelling procedure. We then analyse the influence of local regularization conditioning on inverted models and demonstrate how it improves the clarity and improves the reliability of the interpretation of the buried greenstone belts.
2.1 Inversion methodology
The inversion procedure we propose integrates spatially varying prior information to weight the regularization function locally (e.g. in each cell). It is implemented in an expanded version of the least-square inversion platform TOMOFAST-X (Martin et al., 2013, 2018), which offers the possibility to condition the regularization function (Tikhonov and Arsenin, 1977) of Li and Oldenburg (1996) locally using geological uncertainty. This is achieved by incorporating prior information into a structure-based regularization function in a fashion similar to Brown et al. (2012), Wiik et al. (2015) and Yan et al. (2017) by locally adjusting the related weight.
Solving the inverse problem regularized in this fashion consists of finding a model m that minimizes the objective function θ given below:
where d relates to the geophysical measurements to be inverted, g is the forward modelling operator, m relates to the model being searched for, and mp is the prior model; Wd, Wm and WH are diagonal weighting matrices corresponding to data noise, model weighting and gradient regularization, respectively. The model term is a ridge regression constraint term (Hoerl and Kennard, 1970).
The structural regularization term in Eq. (1) enforces structural constraints during inversion. It is weighted locally by matrix WH, which can be derived from prior information (see Sect. 2.3 for details). The positive free parameters αm and αH control the overall weight of model and structural regularization terms; ∇ is the spatial gradient operator. Note that estimates the amount of structure in inverted physical property model m. Also note that parts of the model where WH=0 are excluded from the calculation of the structural regularization and can change freely to accommodate geophysical data.
We utilize the integrated sensitivity technique of Portniaguine and Zhdanov (2002) to balance the decreasing sensitivity of gravity data with depth. We chose this technique because it offers the advantage of providing “equal sensitivity of the observed data to the cells located at different depths and at different horizontal positions” (Vatankhah and Renaut, 2017).
2.2 Probabilistic geological modelling
Probabilistic geological modelling is performed using the Monte Carlo uncertainty estimator (MCUE) method of (Pakyuz-Charrier et al., 2018a, b), which extends previous works from Jessell et al. (2010), Lindsay et al. (2012) and Wellmann et al. (2010). It is a 3-D uncertainty propagation method for implicit geological modelling that uses geological rules and geological orientation measurements (foliation and interface of the geological units sampled at surface level or in boreholes) as inputs. The sampling algorithm perturbs orientation data used to derive a reference model by sampling probability distributions describing the uncertainty of orientation data to produce a series of unique altered geological models. Realizations that do not respect a series of geological rules are considered implausible and are rejected. Coupled to the 3-D geological modelling engine of Geomodeller© (Calcagno et al., 2008), it produces a set of plausible geological models honouring the geological input measurements that represent the geological model space (Lindsay et al., 2013b). The observation probabilities constituting the probabilistic geological model (PGM) are obtained, in each model cell, by calculating the relative observation frequencies of the different lithologies from the set of geological models. For the ith model cell of a PGM containing L lithologies, vector , …, contains the observation probabilities of each lithology. As we show in the next subsection, the resulting PGM can be used to estimate uncertainty levels and as a source of prior information.
2.3 Utilization of information entropy for local conditioning
Information entropy was introduced for geological modelling by Wellmann and Regenauer-Lieb (2012) and is gaining popularity as a measure of uncertainty in probabilistic geological modelling (de la Varga et al., 2018; de la Varga and Wellmann, 2016; Lindsay et al., 2013, 2014; Pakyuz-Charrier et al., 2018b; Schweizer et al., 2017; Thiele et al., 2016; Wellmann et al., 2017; Yamamoto et al., 2014). Quoting Schweizer et al. (2017), information entropy “quantifies the amount of missing information and hence, the uncertainty at a discrete location”. For the ith model-cell, it is given as follows (Shannon, 1948):
Fundamentally, geological uncertainty contained in H encapsulates information about possible locations of interfaces between units and areas where the geological data are insufficiently informative. Instead of using H directly, we calculate WH by utilizing its normalized complementary, which reflects the degree of certainty across the model. Let us express WH as follows, for the ith model cell:
The consequence of Eqs. (2) and (3) is that WH is minimum at interfaces and in areas poorly constrained by geological information, and equal to unity in areas where the geology is well resolved. Consequently, the conditioning process attaches small weights to the structural term of Eq. (1) in uncertain cells, while consistently high values will be applied to the most geologically certain cells. As a result, it enables the inversion algorithm to favour nearly constant changes in the inverted model in certain contiguous groups of cells (e.g. where WH→1) while relaxing the regularization constraints in the most uncertain parts (e.g. where WH→0).
This section introduces the proof of concept of the proposed method through an idealized case study illustrating the potential of the proposed inverse modelling scheme to ameliorate inversion results and to reduce interpretation uncertainty. We use the same 3-D density contrast model as Giraud et al. (2017), which is obtained by populating the structural framework of Pakyuz-Charrier et al. (2018b). We simulate a series of PGMs sought to represent expected values as well as possible extreme scenarios. The short presentation of the model below and the analysis of results provides essential information about the synthetic survey and shows the proof of concept of the methodology used in the paper.
3.1 Survey set-up
The 3-D unperturbed reference geological model was generated from contact (interface points) and surface orientation (foliations) field measurements collected in the Mansfield area (Victoria, Australia). It presents a Carboniferous mudstone–sandstone basin oriented 170∘ north, abutting a faulted contact with a folded ultramafic basement to the south-west. Model complexity was artificially increased through the addition of a north–south fault and of a mafic intrusion.
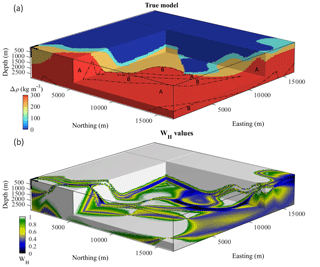
The true density contrast model (Fig. 1a) was obtained by assigning density contrasts consistently with the structural setting of the reference geological model, assuming a flat topography. Density contrasts of 0 and 100 kg m−3 were assigned to the upper and lower basin lithotypes, respectively. Mafic rocks were assigned a density contrast of 200 kg m−3 while the density contrast of the ultramafic basement was set to 300 kg m−3.
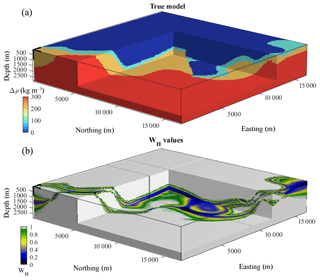
Figure 1True density contrast model and WH values used for local regularization conditioning. (a) Unperturbed reference model populated with density contrast values, (b) uncertainty values used for local regularization conditioning.
MCUE perturbations of the reference geological model were first performed using standard measurement uncertainty values recommended by metrological studies, as reported by Allmendinger et al. (2017) and Novakova and Pavlis (2017). We generated a series of 300 models that were subsequently combined into a PGM. The resulting volume representing the WH values calculated from this PGM in each cell of the model as per Eq. (3) is shown in Fig. 1b.
3.2 Locally constrained inversion: validation
To assess the impact of local conditioning of the regularization function onto inversion, we compare inversions using a non-conditioned (Fig. 2a) and a locally conditioned (Fig. 2b) regularization function, respectively. Please note that when simulating the absence of prior petrophysical information, a homogenous prior model set to 0 kg m−3 was used in both cases.
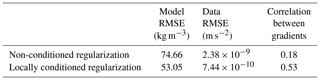
Besides qualitative visual comparison of the models, we interpret inversion results (Fig. 2) through the commonly used model and data root-mean-square errors (RMSEs), which correspond to the model and data terms calculated with weights and covariances set to unity. We evaluate the geometrical similarity between inverted and true model through the Bravais–Pearson correlation (also often called “linear correlation coefficient”) between their gradients (Table 1).
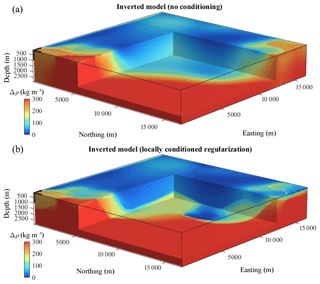
Figure 2Comparison of inversion results. (a) Inverted models with non-conditioned regularization weights, and (b) using local conditioning.
Comparison of the true model (Fig. 1a) with inversion results in Fig. 2a and b shows that, while the structures in the shallowest part of the model are well retrieved in both cases, it appears that they are considerably better recovered through usage of conditioned regularization overall (Fig. 2b). The guiding effect of WH is visible in Fig. 2b where the main structures at depth follow the general features of the conditioning volume (Fig. 1b). Moreover, in order to minimize the conditioned regularization constraint simultaneously to data misfit, inversion was driven to accommodate inverted model values (Fig. 2b) such that they are closer to the causative model (Fig. 1a) than without conditioning (Fig. 2a). This leads to reduced model RMSE on the one hand, and increased data RMSE on the other (Table 1). This reduction in data RMSE can also be explained by the relaxation of the constraints in several portions of the model, thus increasing the degree of liberty to accommodate the model towards lower data misfit. More importantly, the Bravais–Pearson correlation between the inverted and true model gradients is much higher when information from information entropy is used. This indicates that local conditioning of the regularization function also allows for significantly better retrieval of the causative bodies' (e.g. the true model) structural features.
Please also note that we do not show the recovered geophysical measurements because visual differences between recovered and inverted measurements are minimal.
From these observations, we conclude that the application of the local conditioning scheme can fulfil the objectives of data integration in inversion as it allows inversion to recover models that are closer to the causative bodies and easier to interpret, while honouring geophysical data. Nevertheless, it remains important to test the methodology in cases where the uncertainty indicator WH is biased and/or shows high-geological-uncertainty levels away from faults and contacts. As a thorough analysis lies beyond the scope of this paper, the remainder of this section presents an elementary sensitivity analysis using a series of two WH volumes representing distinct extreme scenarios.
3.3 Inversion constrained by biased geological uncertainty model
In this subsection, we investigate the effect of inaccurate geological models and the propagation of the related uncertainty in inversion. For this purpose, we calculate a second PGM from MCUE perturbations in which we split the ultramafic basement into two independent units, without changing the density contrast values (Fig. 3a). This results in the existence of a fictitious geological unit that is invisible to gravity data and presents no density contrast but which increases geological complexity and uncertainty (Fig. 3b) (we further refer to it as a “ghost” geological unit). Notably, it increases geological uncertainty and smears interfaces that are well-constrained as per Fig. 1. It also decreases WH in large parts of the model where WH→1 previously, thereby favouring model changes in these areas during inversion and encouraging it to place larger density contrast or interfaces in these areas.
Comparison of the inverted models obtained without (Fig. 4a) and with the ghost unit (Fig. 4b) reveals that they exhibit broadly similar features except in the most geologically complex parts of the model as per Fig. 1b, where differences are minor. This indicates that while geophysical inversion updates the prior density contrast model preferably in geologically uncertain regions, low values of WH do not necessarily lead to the modelling of an interpretable interface by inversion. From the comparison of Figs. 3b and 4b, we can deduce that local conditioning as applied in this work does not necessarily enforce strict structural similarity between the inverted model and the conditioning geological uncertainty volume.
3.4 Inversion constrained using exaggerated geological uncertainty
To complete this series of tests, we generated a third PGM showing exaggerated geological uncertainty. To this end, we used a half-aperture 95 % confidence interval of ∼50∘ for orientation data measurements in our MCUE simulations. This is far higher than for the rest of the MCUE simulations used in this paper. All other simulations (Sect. 3.2 and 3.3) use a value of ∼11∘, which is representative of realistic measurement uncertainty as proposed by recent metrological studies (Allmendinger et al., 2017; Cawood et al., 2017; Novakova and Pavlis, 2017). Figure 5 shows the resulting WH volume (Fig. 5a) and the inverted model obtained by using it for local conditioning of the regularization constraint (Fig. 5b).
The features visible in Fig. 5a reflect the high geological input measurement uncertainty. Geologically uncertain areas cover large portions of the volume and only the simplest geological structures (e.g. the basin) seem to be well constrained by geology. Areas of the model previously well constrained (Fig. 1b) present varying degrees of uncertainty. This illustrates that, as can be expected, increasing geological input uncertainty translates in relaxing the guiding effect of local conditioning using WH, which results in geophysical inversion being less strongly guided by geological information. As can be seen in Fig. 4b, the inverted model obtained in this case shows structures that present weaker contrast around interfaces than when geological uncertainty is lower (Fig. 2b). Importantly, however, most structures are well preserved and the overall model values for the different lithologies remain closer to the true model than for the non-conditioned case (Fig. 2a). This indicates that even in high geological uncertainty scenarios, interpretation outcome may be largely more reliable when local regularization is used.
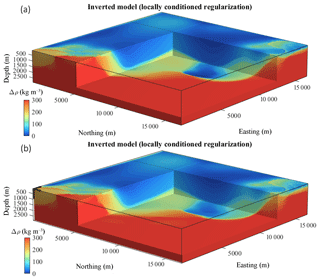
Figure 4Comparison of inverted model using WH derived from a PGM considering the ghost unit (b) and without it (a); (a) is the inverse model obtained without bias in the PGM as per Fig. 2 and is shown here for comparison with (b).
The analysis and comparison of the results shown in this section demonstrates the potential of the proposed inverse modelling scheme to ameliorate inversion results and to reduce interpretation uncertainty. It also illustrates the capability of our methodology to deal with high or biased conditioning uncertainty estimates. In this synthetic case, local conditioning allows geophysical inversion to significantly improve the imaging of geologically uncertain areas and to exploit complementarities between geological modelling and geophysical inversion. From the success of this proof-of-concept study, we are confident that our integration method can be tested here using real world data for field validation.
4.1 Geological context and geophysical survey set-up
The Yerrida Basin is located in the southern part of the Capricorn Orogen, at the northern margin of the Yilgarn Craton in Western Australia (Fig. 6a), and extends approximately 150 km N–S and 180 km E–W (Fig. 6b). The studied area is bounded in the north-west by the Goodin Fault, which represents a faulted contact between the Yerrida Basin and the Bryah–Padbury Basin. The structures of interest in this work are the Archean greenstone belts extending north-northwest that are unconformably overlain by Paleoproterozoic sedimentary rocks the form the Yerrida Basin. Features A and B (Fig. 6a and b) indicate the interpreted position of buried Wiluna Greenstone Belt. Where the Wiluna Greenstone Belt is exposed, it is host to base and precious metal mineralization (Williams, 2009). With a relatively high positive density contrast (expected to be between 190 and 270 kg m−3) to the Yilgarn Craton granite–gneiss host, mafic greenstone belts A–C are suitable targets for gravity inversion. Interpretations from multiple studies in the region, e.g. Johnson et al. (2013), Pirajno et al. (1998), Pirajno and Adamides (2000), and Pirajno and Occhipinti (2000) were compiled, while additional geological measurements acquired in 2015–2017 complemented legacy data (Occhipinti et al., 2017; Olierook et al., 2018). This allowed the revision of existing models and improved our understanding of the area. This, in turn, also highlights the challenges presented by the characterization of greenstone belts A–C, and that further geophysical analysis through constrained inversion is a useful pathway for reducing exploration risk.
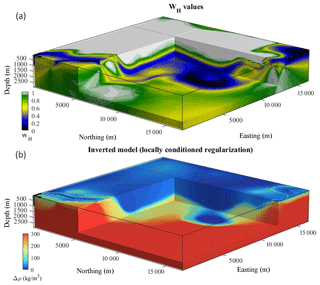
Figure 5(a) Local weights WH calculated from a PGM, corresponding to exaggerated uncertainty in geological input measurements and (b) corresponding inverted density contrast model.
Geophysical data consist of ground surveys obtained from Geoscience Australia (http://www.ga.gov.au/data-pubs, last access: November 2018). Post-processing includes spherical-cap and terrain corrections and the removal of the regional trend to obtain the complete Bouguer anomaly. As most data points were acquired 1 to 4 km apart, the dataset was resampled to match the geological model discretization, making up a total of 4882 measurement points. The model is discretized into cells of dimensions 2.335 km × 1.875 km × 1.0475 km, down to a depth of 44 km, making up a total of 420 000 cells.
4.2 Geological modelling
Geological information consists of in situ structural measurements (interfaces and foliations) and interpretation of aeromagnetic, airborne electromagnetic, Landsat 8 and ASTER hyperspectral data. Legacy data from the Geological Survey of Western Australia (Pirajno and Adamides, 2000) and CSIRO (Ley-Cooper et al., 2017) were used, to which about 600 surface geological and petrophysical measurements from recent geological field campaigns were added. Although the available petrophysical measurements were not used to derive petrophysical constraints because of the insufficient sampling of several of the modelled lithologies, they were a useful source of information to populate geological models and for interpretation. Remote-sensing data were used to test interpretations.
These datasets were used jointly to build a reference geological model reconciling the available geological information in Geomodeller.
Lithologies with similar density contrasts were merged and subsequently treated as a single rock type in MCUE simulations. Uncertainty related to structural measurements was subsequently used as inputs to the MCUE perturbations (Pakyuz-Charrier et al., 2018b) of the reference model to generate a collection of 500 accepted models. Information extracted from the PGM is displayed in Fig. 7. Figure 7a shows the lithologies with the highest probability for each cell of the PGM. The associated WH values used in inversion are shown in Fig. 7b. The prior model for inversion mp is equal to the mean model of the 500 plausible models generated by MCUE. It is shown in Fig. 7c.
4.3 Inversion results and analysis
The aim of our analysis is to assess the influence of the local conditioning of structural constraints on inversion through comparison with the non-conditioned case, all other things remaining constant.
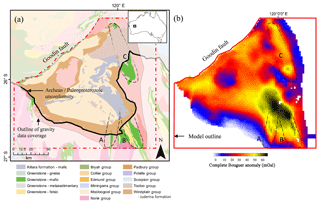
Figure 6Geological context and geophysical data. (a) Geological map of the area and (b) complete Bouguer anomaly. The dashed lines delineate the possible sub-basin extent of the mafic greenstone belts A–C.
4.3.1 Comparative analysis strategy
Prior to examination of the inverted models, we analyse geophysical data misfit after inversion. This enables us to ensure that the inversion results we compare produce, in our case, similar gravity anomalies. Our study of inverted models focuses on results obtained through usage of non-conditioned (Fig. 8a) and conditioned regularization functions (Fig. 8b) using WH (Fig. 7b). In addition to departures from the prior model, variations between the two cases are studied by visual comparison of Figs. 8a and 7b, through qualitative (Fig. 7c) and quantitative comparative analysis (Fig. 7d and e). Our interpretation of inversion results is complemented by metrics quantifying the differences between models. We give particular attention to model cells where the probability of mafic greenstone is larger than zero. For these cells, we classify lithologies by identifying cells with a density contrast corresponding to mafic greenstone.
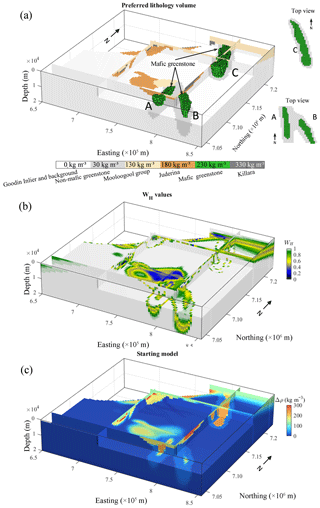
Figure 7Geological modelling results. (a) Most probable (i.e. preferred) lithology in each model cell (same colour code as in Fig. 6), (b) values used for local regularization conditioning, and (c) prior model derived from PGM and prior petrophysical information. In (a), “background” refers to all the lithologies that have a density contrast equal to 0 kg m−3.
4.3.2 Results
Data root-mean-square (RMS) error decreases during inversion from 12.46 mGal to reach 1.59 and 1.53 mGal for the non-conditioned and conditioned cases, respectively. The corresponding data misfit maps show a linear correlation coefficient of 0.999 (see details in Appendix A). This similarity illustrates that, as in many other studies, most changes related to holistic data integration in geophysical inversion occur primarily in model space, hence reducing the effect of non-uniqueness (Abtahi et al., 2016; Abubakar et al., 2012; Brown et al., 2012; Demirel and Candansayar, 2017; Gallardo et al., 2012; Gallardo and Meju, 2004, 2007, 2011; Gao et al., 2012; Giraud et al., 2017; Guo et al., 2017; Heincke et al., 2017; Jardani et al., 2013; Juhojuntti and Kamm, 2015; Kalscheuer et al., 2015; Molodtsov et al., 2013; Moorkamp et al., 2013; Rittgers et al., 2016; Sun and Li, 2016, 2017).
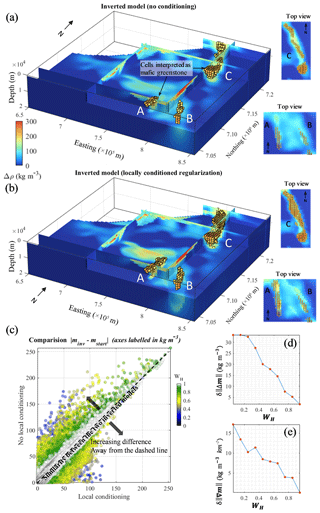
Figure 8Comparison of inversion results. (a) Inverted models with non-conditioned regularization weights, and (b) using local conditioning, (c) cross-plot between the corresponding absolute value of the update of the prior model, (d) difference in model updates as a function of values of WH and (e) difference in model roughness as a function of values of WH. The model cells labelled A–C are interpreted as mafic greenstone belts. All voxels are coloured as a function of density contrast.
Qualitatively, comparison of Fig. 8a and b reveals that departures from the prior model (Fig. 7c) are more significant in the most geologically uncertain areas. Quantitatively, the RMS model update for cells characterized by (most uncertain group) is equal to 40.1 and 51.5 kg m−3, for the non-conditioned and conditioned cases, respectively, whereas the same quantities are equal to 17.7 and 16.9 kg m−3 for the cells identified by (most certain group). This suggests that local regularization conditioning allows inversion to update the model preferentially in geologically uncertain areas. In turn, differences with the prior model in more geologically certain areas are reduced compared to the non-conditioned case. This effect of conditioning is corroborated by Fig. 8c, in which the longest distances to the dashed line, which represents equal model update for the two studied cases, occur in geologically uncertain areas. This also translates into a higher difference between model updates of the two cases in Fig. 7d for lower values of WH. In addition, we observe that local conditioning produces stronger density contrasts in Fig. 8b in some of the areas where the conditioning values are higher in Fig. 8b. Furthermore, structures in the inverted model are easier to identify when local conditioning is used. It is confirmed by global roughness measures equal to 3.4 and 4 ( (kg m−3 m−1) for the non-conditioned and conditioned cases, respectively. More specifically, as shown by Fig. 7e, this difference arises in parts of the model associated with lower WH, which characterize uncertain areas, including interfaces between lithologies.
The recovered greenstone belts are shown in Fig. 8a and b. In Fig. 8b, the extension of recovered mafic greenstone belts is significantly different than when geological uncertainty is not accounted for (Fig. 8a). In particular, belt A is significantly larger in Fig. 8b than in Fig. 8a (2.4×102 km3 vs. 4.6×102 km3). Similarly, the extent of belt C is increased overall (volume of 5.3×102 km3 vs. 14×102 km3), while its different portions reconnect; the northern half is also significantly shallower and broader than in Figs. 7a and 8a. It appears that belt A remains thinner and shallower (Fig. 8b) than suggested by the preferred lithology volume (Fig. 7a). While similar geometries for belt B are recovered in Fig. 8a and b, they both differ from Fig. 7a as only the eastern part is preserved. Note that it is larger in Fig. 8b, with a volume 40 % higher than in Fig. 8a. As discussed in the next subsection, these differences have a signification impact on the interpretation of inversion results and are important to understand the influence of local conditioning on inversion.
4.4 Interpretation
Note that, in contrast to the differences between inversion results highlighted above for belts A and C, there are only small differences between the inverted models in the north-eastern part of the model and the different interpretations of belt B (Fig. 7a and b). This shows that locally conditioned regularization does not enforce changes in the inverted model in all places where geological uncertainty is high, as uncertainty is only a reflection of potential errors. Rather, this indicates that in such cases, the guiding effect of such regularization will be exerted on the condition that it does not prevent the data term in θ(d, m) as per Eq. (1) from decreasing. This also confirms that geophysical data are the main driver of the model updates in geologically uncertain areas. Instead of smooth departures from the prior model to match geophysical data regardless of geological considerations, local regularization constraints allow inversion to account for the probabilistic geological modelling of the area and for geological uncertainty. It can therefore provide results that conform better to known geology.
In consequence, by confronting a probabilistic geological model encapsulating all MCUE realizations with geophysical measurements in an inversion scheme favouring model updates in the most geologically uncertain areas, inversion complements probabilistic geological modelling in that it guides and refines the interpretation of other geoscientific data in the area.
Geophysical inversion using geological uncertainty information (Fig. 7b) confirms the presence of high-density anomalies that we interpret to be the mafic components of the greenstone as suggested by MCUE in several portions of the model. It also adjusts the outline and geometry of belts A–C to obtain a model honouring geological uncertainty information. In particular, mafic greenstone belts A and B may be smaller than the extent suggested by the PGM, and mafic greenstone C shallower than anticipated. The interpretation of inversion results also reveals that greenstone B might extend further to the east than indicated by the preferred lithology volume (Fig. 7a) and that greenstone C may be thinner in its central part.
We have introduced a new integration scheme for the inversion of gravity data that utilizes a measure of geological uncertainty to calculate locally conditioned gradient regularization constraints. This approach enables the integration of probabilistic geological modeling in geophysical inversion in the absence of petrophysical information sufficient to the calculation of petrophysical constraints. It uses geophysical measurements to optimize the inverse problem by updating the physical property model preferably in geologically uncertain parts of the studied area during what we called uncertainty-guided inversion. This therefore partly mitigates the non-uniqueness of the inversion through the addition of constraints encouraging inversion to produce models that account for geological uncertainty across the entire inverted volume. We have demonstrated that it can be used collaboratively with geological modelling efficiently through field application in the Yerrida Basin. Inversion results show that our integration methodology has the capability to refine the recovered physical property model and interpretations in portions of the model where geological uncertainty is high. Another advantage of the proposed technique is that it is time- and cost-effective as our workflow utilizes the PGM resulting from standalone probabilistic geological modelling and requires the same parameterization as non-conditioned inversion.
In the Yerrida Basin study area, application of the proposed methodology provided the effective delineation of the greenstone belts by quantitatively integrating geological measurements and geophysical data. Our findings suggest that some of the greenstone belts covered by the basin might be shallower than previously anticipated and occupy smaller volumes. This is particularly pronounced in the north-east (belt C), where the resulting model is in agreement with the shallowest cases allowed by the PGM. Likewise, in the south (belt A), only the shallowest part of the mafic greenstone body can be resolved, while the south-eastern (belt B) greenstone belt appears to be limited in extension to the eastern part of the volume where it is the preferred lithology in the PGM. In such cases, this can also indicate that these greenstone bodies might be too thin to be imaged by gravity data. These results have implications for our knowledge of the southern Capricorn Orogen as they indicate reduced (compared to the preferred lithology volume) mafic greenstone volumes under the Yerrida Basin on the one hand, and decreased cover thickness on the other hand, thereby opening the door to updates in the geological interpretation of geometry of the Yerrida Basin and potential new undercover exploration prospects.
The quantitative integration technique we presented reduces uncertainty and ambiguity compared to qualitative interpretation techniques or single-discipline workflows. However, despite its robustness to misplaced interfaces (e.g. bias) or to high geological uncertainty (e.g. sparse or very uncertain geological input measurements) as shown in the synthetic case, interpreters need to bear in mind the specificities of the geophysical data inverted for (resolution of specific geometries, depth of investigation) and the shortcomings of geological modelling workflows. As for all geological modelling, MCUE is oblivious to geological units or faults that are not sampled by field geological measurements, which can lead to biases in final models due to, for instance, inclusions not be accounted for.
Current research comprises the development of sensitivity and resolution analyses in an effort to mitigate the risk of the model being affected by uncertainty sources not accounted for. Future research will include the utilization of local petrophysical constraints of Giraud et al. (2017) in the uncertainty-guided inversion scheme we presented, as well as the utilization of geological uncertainty to weight the cross-gradient term of Gallardo and Meju (2003) locally. With this last respect, uncertainty-guided inversion can be assisted in the most uncertain parts of the model by guided inversion (in the sense of Brown et al., 2012) or through cross-gradient joint inversion.
True property models, inversion results and recovered models relating to the Yerrida Basin shown in this article are made available online at https://doi.org/10.5281/zenodo.1238216 (Giraud et al., 2018a). True property models, inversion results and recovered models relating to the synthetic case from the Mansfield area shown in this article are made available online at https://doi.org/10.5281/zenodo.1238529 (Giraud et al., 2018a).
Figure A1 below relates to the analysis of data misfit in Sect. 4 of the article through the plot of the data misfit maps for the non-conditioned and conditioned cases (Fig. A1d and h, respectively). It is complemented by the corresponding plots of starting (Fig. A1a and e), observed (Fig. A1b and f) and calculated data (Fig. A1c and h). Note that Fig. A1c and g show few visual differences, and that Fig. A1d and h exhibit similar features while showing limited coherent signal.
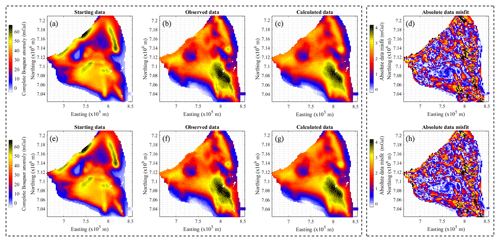
Figure A1Comparison of input and output geophysical data. Panels (a) and (e) show data calculated from the prior model, (b) and (f) input measurements, (c) and (g) data calculated from the inverted model, and (d) and (f) the absolute value of the difference of the misfit between the observed and calculated data. Panels (a–d) (i.e. first line) and (e–h) (i.e. second line) correspond to the non-conditioned and conditioned cases, respectively.
JG performed the integrated inverse modelling of geophysical data for both the Mansfield synthetic study and the Yerrida Basin. He performed posterior analysis and interpretation of results and he is the main contributor to the writing of this article. ML acquired part of the geological field measurements from the Yerrida Basin and performed the geological modelling of the area. He participated in the writing of the geological setting subsection and he produced the geological map shown in Fig. 6a. VO and JG worked together on the implementation and testing of the proposed methodology in TOMOFAST-X, of which VO, RM and JG are the main developers. MJ has been involved in the validation of the methodology at the initial development stage and supervised the progress of the presented work. RM provided support at the initial stage of the inversion of gravity data from the Yerrida Basin. EP-C assisted ML with the utilization of MCUE. All co-authors contributed to the final version of this article. ML and VO were the most actively involved in the revision process of the drafts leading to this paper.
The authors declare that they have no conflict of interest.
Appreciation is expressed to the CALMIP supercomputing centre (Toulouse,
France), for their support through Roland Martin's computing projects no. P1138_2017 and no. P1138_2018 and for the
computing time provided on the EOS machine. Jeremie Giraud is a recipient of
the International Postgraduate Research Scholarship from the Australian
Federal Government and he received a grant from the Australian Society of
Exploration Geophysics Research Foundation. The authors also thank Peter Lelievre
for interesting discussions and constructive feedback relating to
the utilization of gradient-related constraints. Mark D. Lindsay and
Mark W. Jessell thank the Geological Survey of Western Australia (Royalties for
Regions Exploration Incentive Scheme) and the Minerals Research Institute of
Western Australia for their support. Mark W. Jessell is supported by a
Western Australian Fellowship. The authors acknowledge use of the Zenodo
research date repository to share the data necessary to reproduce the
presented work. They finally thank Colin Farquharson and an anonymous
reviewer for their review of the paper.
Edited by: Michal Malinowski
Reviewed by: Colin Farquharson and one anonymous referee
Abtahi, S. M., Pedersen, L. B., Kamm, J., and Kalscheuer, T.: Case History Extracting geoelectrical maps from vintage very-low-frequency airborne data, tipper inversion, and interpretation: A case study from northern Sweden, Geophysics, 81, B135–B147, https://doi.org/10.1190/geo2015-0296.1, 2016.
Abubakar, A., Gao, G., Habashy, T. M., and Liu, J.: Joint inversion approaches for geophysical electromagnetic and elastic full-waveform data, Inverse Probl., 28, 055016, https://doi.org/10.1088/0266-5611/28/5/055016, 2012.
Allmendinger, R. W., Siron, C. R., and Scott, C. P.: Structural data collection with mobile devices: Accuracy, redundancy, and best practices, J. Struct. Geol., 102, 98–112, https://doi.org/10.1016/j.jsg.2017.07.011, 2017.
Brown, V., Key, K., and Singh, S.: Seismically regularized controlled-source electromagnetic inversion, Geophysics, 77, E57–E65, https://doi.org/10.1190/geo2011-0081.1, 2012.
Calcagno, P., Chilès, J. P., Courrioux, G., and Guillen, A.: Geological modelling from field data and geological knowledge. Part I. Modelling method coupling 3D potential-field interpolation and geological rules, Phys. Earth Planet. Inter., 171, 147–157, https://doi.org/10.1016/j.pepi.2008.06.013, 2008.
Cawood, A. J., Bond, C. E., Howell, J. A., Butler, R. W. H., and Totake, Y.: LiDAR, UAV or compass-clinometer? Accuracy, coverage and the effects on structural models, J. Struct. Geol., 98, 67–82, https://doi.org/10.1016/j.jsg.2017.04.004, 2017.
de la Varga, M. and Wellmann, J. F.: Structural geologic modeling as an inference problem: A Bayesian perspective, Interpretation, 4, SM1–SM16, https://doi.org/10.1190/INT-2015-0188.1, 2016.
de la Varga, M., Schaaf, A., and Wellmann, F.: GemPy 1.0: open-source stochastic geological modeling and inversion, Geosci. Model Dev. Discuss., https://doi.org/10.5194/gmd-2018-61, in review, 2018.
Demirel, C. and Candansayar, M. E.: Two-dimensional joint inversions of cross-hole resistivity data and resolution analysis of combined arrays, Geophys. Prospect., 65, 876–890, https://doi.org/10.1111/1365-2478.12432, 2017.
Dentith, M. and Mudge, S. T.: Geophysics for the mineral exploration geologist, Cambridge University Press, Cambridge, UK, 2014.
Gallardo, L. A. and Meju, M. A.: Characterization of heterogeneous near-surface materials by joint 2D inversion of dc resistivity and seismic data, Geophys. Res. Lett., 30, 1658, https://doi.org/10.1029/2003GL017370, 2003.
Gallardo, L. A. and Meju, M. A.: Joint two-dimensional DC resistivity and seismic travel time inversion with cross-gradients constraints, J. Geophys. Res.-Solid, 109, B03311, https://doi.org/10.1029/2003JB002716, 2004.
Gallardo, L. A. and Meju, M. A.: Joint two-dimensional cross-gradient imaging of magnetotelluric and seismic traveltime data for structural and lithological classification, Geophys. J. Int., 169, 1261–1272, https://doi.org/10.1111/j.1365-246X.2007.03366.x, 2007.
Gallardo, L. A. and Meju, M. A.: Structure-coupled multiphysics imaging in geophysical sciences, Rev. Geophys., 49, RG1003, https://doi.org/10.1029/2010RG000330, 2011.
Gallardo, L. A., Fontes, S. L., Meju, M. A., Buonora, M. P., and de Lugao, P. P.: Robust geophysical integration through structure-coupled joint inversion and multispectral fusion of seismic reflection, magnetotelluric, magnetic, and gravity images: Example from Santos Basin, offshore Brazil, Geophysics, 77, B237–B251, https://doi.org/10.1190/geo2011-0394.1, 2012.
Gao, G., Abubakar, A., and Habashy, T. M.: Joint petrophysical inversion of electromagnetic and full-waveform seismic data, Geophysics, 77, WA3, https://doi.org/10.1190/geo2011-0157.1, 2012.
Giraud, J., Jessell, M., Lindsay, M., Parkyuz-Charrier, E., and Martin, R.: Integrated geophysical joint inversion using petrophysical constraints and geological modelling, in: SEG Technical Program Expanded Abstracts 2016, Society of Exploration Geophysicists, Houston, TX, 1597–1601, 2016.
Giraud, J., Pakyuz-Charrier, E., Jessell, M., Lindsay, M., Martin, R., and Ogarko, V.: Uncertainty reduction through geologically conditioned petrophysical constraints in joint inversion, Geophysics, 82, ID19–ID34, https://doi.org/10.1190/geo2016-0615.1, 2017.
Giraud, J., Lindsay, M., and Ogarko, V.: Yerrida Basin Geophysical Modeling – Input data and inverted models, Version version 1.0, Data set, Zenodo, https://doi.org/10.5281/zenodo.1238216, 2018a.
Giraud, J., Ogarko, V., and Pakyuz-Charrier, V.: Synthetic dataset for the testing of local conditioning of regularization function using geological uncertainty, Version version 1.0, Data set, Zenodo, https://doi.org/10.5281/zenodo.1238529, 2018b.
Guillen, A., Calcagno, P., Courrioux, G., Joly, A., and Ledru, P.: Geological modelling from field data and geological knowledge. Part II. Modelling validation using gravity and magnetic data inversion, Phys. Earth Planet. Inter., 171, 158–169, https://doi.org/10.1016/j.pepi.2008.06.014, 2008.
Guo, Z., Dong, H., and Kristensen, Å.: Image-guided regularization of marine electromagnetic inversion, Geophysics, 82, E221–E232, https://doi.org/10.1190/geo2016-0130.1, 2017.
Haber, E. and Oldenburg, D.: Joint inversion: a structural approach, Inverse Probl., 13, 63–77, https://doi.org/10.1088/0266-5611/13/1/006, 1997.
Heincke, B., Jegen, M., Moorkamp, M., Hobbs, R. W., and Chen, J.: An adaptive coupling strategy for joint inversions that use petrophysical information as constraints, J. Appl. Geophys., 136, 279–297, https://doi.org/10.1016/j.jappgeo.2016.10.028, 2017.
Hoerl, A. E. and Kennard, R. W.: Ridge Regression: Application to nonorthogonal problems, Technometrics, 12, 69–82, https://doi.org/10.1080/00401706.1970.10488634, 1970.
Jardani, A., Revil, A., and Dupont, J. P.: Stochastic joint inversion of hydrogeophysical data for salt tracer test monitoring and hydraulic conductivity imaging, Adv. Water Resour., 52, 62–77, https://doi.org/10.1016/j.advwatres.2012.08.005, 2013.
Jessell, M. W., Ailleres, L., and de Kemp, E. A.: Towards an integrated inversion of geoscientific data: What price of geology?, Tectonophysics, 490, 294–306, https://doi.org/10.1016/j.tecto.2010.05.020, 2010.
Jessell, M. W., Aillères, L., De Kemp, E., Lindsay, M., Wellmann, F., Hillier, M., Laurent, G., Carmichael, T., and Martin, R.: Next Generation Three-Dimensional Geologic Modeling and Inversion, SEG Spec. Publ. 18, chap. 13, SEG, Keystone, CO, USA, 261–272, 2014.
Jessell, M. W., Pakyuz-charrier, E., Lindsay, M., Giraud, J., and de Kemp, E.: Assessing and Mitigating Uncertainty in Three-Dimensional Geologic Models in Contrasting Geologic Scenarios, SEG Special Publications no. 21, SEG, Keystone, CO, USA, 63–74, https://doi.org/10.5382/SP.21.04, 2018.
Johnson, S. P., Thorne, A. M., Tyler, I. M., Korsch, R. J., Kennett, B. L. N., Cutten, H. N., Goodwin, J., Blay, O., Blewett, R. S., Joly, A., Dentith, M. C., Aitken, A. R. A., Holzschuh, J., Salmon, M., Reading, A., Heinson, G., Boren, G., Ross, J., Costelloe, R. D., and Fomin, T.: Crustal architecture of the Capricorn Orogen, Western Australia and associated metallogeny, Aust. J. Earth Sci., 60, 681–705, https://doi.org/10.1080/08120099.2013.826735, 2013.
Juhojuntti, N. and Kamm, J.: Joint inversion of seismic refraction and resistivity data using layered models – Applications to groundwater investigation, Geophysics, 80, EN43–EN55, https://doi.org/10.1190/geo2013-0476.1, 2015.
Kalscheuer, T., Blake, S., Podgorski, J. E., Wagner, F., Green, A. G., Maurer, H., Jones, A. G., Muller, M., Ntibinyane, O., and Tshoso, G.: Joint inversions of three types of electromagnetic data explicitly constrained by seismic observations: results from the central Okavango Delta, Botswana, Geophys. J. Int., 202, 1429–1452, https://doi.org/10.1093/gji/ggv184, 2015.
Lelièvre, P. G. and Farquharson, C. G.: Integrated Imaging for Mineral Exploration, in: Integrated Imaging of the Earth: Theory and Applications, John Wiley & Sons, Inc., New York, 137–166, 2016.
Lelièvre, P. G., Farquharson, C., and Hurich, C.: Joint inversion of seismic traveltimes and gravity data on unstructured grids with application to mineral exploration, Geophysics, 77, K1–K15, https://doi.org/10.1190/geo2011-0154.1, 2012.
Ley-Cooper, A.-Y., Munday, T., and Ibrahimi, T.: Inversion of the Capricorn Orogeny regional Airborne Electromagnetic (AEM) survey, Western Australia, CSIRO Technical Report EP166290, CSIRO, Perth, WA, 2017.
Li, Y. and Oldenburg, D. W.: 3-D inversion of magnetic data, Geophysics, 61, 394–408, https://doi.org/10.1190/1.1443968, 1996.
Lindsay, M. D., Aillères, L., Jessell, M. W., de Kemp, E. A., and Betts, P. G.: Locating and quantifying geological uncertainty in three-dimensional models: Analysis of the Gippsland Basin, southeastern Australia, Tectonophysics, 546–547, 10–27, https://doi.org/10.1016/j.tecto.2012.04.007, 2012.
Lindsay, M. D., Perrouty, S., Jessell, M. W., and Aillères, L.: Making the link between geological and geophysical uncertainty: geodiversity in the Ashanti Greenstone Belt, Geophys. J. Int., 195, 903–922, https://doi.org/10.1093/gji/ggt311, 2013a.
Lindsay, M. D., Jessell, M. W., Ailleres, L., Perrouty, S., de Kemp, E., and Betts, P. G.: Geodiversity: Exploration of 3D geological model space, Tectonophysics, 594, 27–37, https://doi.org/10.1016/j.tecto.2013.03.013, 2013b.
Lindsay, M. D., Perrouty, S., Jessell, M., and Ailleres, L.: Inversion and Geodiversity: Searching Model Space for the Answers, Math. Geosci., 46, 971–1010, https://doi.org/10.1007/s11004-014-9538-x, 2014.
Martin, R., Monteiller, V., Komatitsch, D., Perrouty, S., Jessell, M., Bonvalot, S., and Lindsay, M.: Gravity inversion using wavelet-based compression on parallel hybrid CPU/GPU systems: application to southwest Ghana, Geophys. J. Int., 195, 1594–1619, https://doi.org/10.1093/gji/ggt334, 2013.
Martin, R., Ogarko, V., Komatitsch, D., and Jessell, M.: Parallel three-dimensional electrical capacitance data imaging using a nonlinear inversion algorithm and Lp norm-based model regularization, Measurement, 128, 428–445, https://doi.org/10.1016/j.measurement.2018.05.099, 2018.
Molodtsov, D. M., Troyan, V. N., Roslov, Y. V., and Zerilli, A.: Joint inversion of seismic traveltimes and magnetotelluric data with a directed structural constraint, Geophys. Prospect., 61, 1218–1228, https://doi.org/10.1111/1365-2478.12060, 2013.
Moorkamp, M., Roberts, A. W., Jegen, M., Heincke, B., and Hobbs, R. W.: Verification of velocity-resistivity relationships derived from structural joint inversion with borehole data, Geophys. Res. Lett., 40, 3596–3601, https://doi.org/10.1002/grl.50696, 2013.
Novakova, L. and Pavlis, T. L.: Assessment of the precision of smart phones and tablets for measurement of planar orientations: A case study, J. Struct. Geol., 97, 93–103, https://doi.org/10.1016/j.jsg.2017.02.015, 2017.
Occhipinti, S., Hocking, R., Lindsay, M., Aitken, A., Copp, I., Jones, J., Sheppard, S., Pirajno, F., and Metelka, V.: Paleoproterozoic basin development on the northern Yilgarn Craton, Western Australia, Precambrian Res., 300, 121–140, https://doi.org/10.1016/j.precamres.2017.08.003, 2017.
Olierook, H. K. H., Sheppard, S., Johnson, S. P., Occhipinti, S. A., Reddy, S. M., Clark, C., Fletcher, I. R., Rasmussen, B., Zi, J. W., Pirajno, F., LaFlamme, C., Do, T., Ware, B., Blandthorn, E., Lindsay, M., Lu, Y. J., Crossley, R. J., and Erickson, T. M.: Extensional episodes in the Paleoproterozoic Capricorn Orogen, Western Australia, revealed by petrogenesis and geochronology of mafic–ultramafic rocks, Precambrian Res., 306, 22–40, https://doi.org/10.1016/j.precamres.2017.12.015, 2018.
Paasche, H. and Tronicke, J.: Cooperative inversion of 2D geophysical data sets: A zonal approach based on fuzzy c-means cluster analysis, Geophysics, 72, A35–A39, https://doi.org/10.1190/1.2670341, 2007.
Pakyuz-Charrier, E., Giraud, J., Ogarko, V., Lindsay, M., and Jessell, M.: Drillhole uncertainty propagation for three-dimensional geological modeling using Monte Carlo, Tectonophysics, 747–748, 16–39, https://doi.org/10.1016/j.tecto.2018.09.005, 2018a.
Pakyuz-Charrier, E., Lindsay, M., Ogarko, V., Giraud, J., and Jessell, M.: Monte Carlo simulation for uncertainty estimation on structural data in implicit 3-D geological modeling, a guide for disturbance distribution selection and parameterization, Solid Earth, 9, 385–402, https://doi.org/10.5194/se-9-385-2018, 2018b.
Pears, G., Reid, J., and Chalke, T.: Advances in Geologically Constrained Modelling and Inversion Strategies to Drive Integrated Interpretation in Mineral Exploration, in: Proceedings of Exploration 17: Sixth Decennial International Conference on Mineral Exploration, edited by: Tschirhart, V. and Thomas, V., Toronto. 221–238, available at: http://www.dmec.ca/getattachment/e27f3192-d38e-4d8a-a5f2-404e5d4ca632/Resources/Exploration-17/Iterative-Forward-Modelling-and-Inversion-of-Geoph.aspx (last access: 17 January 2019), 2017.
Pirajno, F. and Adamides, N. G.: Geology and Mineralization of the Palaeoproterozoic Yerrida Basin, Western Australia, Perth, available at: https://catalogue.nla.gov.au/Record/524116 (last access: 17 January 2019), 2000.
Pirajno, F. and Occhipinti, S. A.: Three Palaeoproterozoic basins – Yerrida, Bryah and Padbury – Capricorn Orogen, Western Australia, Aust. J. Earth Sci., 47, 675–688, https://doi.org/10.1046/j.1440-0952.2000.00800.x, 2000.
Pirajno, F., Occhipinti, S. A., and Swager, C. P.: Geology and tectonic evolution of the Palaeoproterozoic Bryah, Padbury and Yerrida Basins (formerly Glengarry Basin), Western Australia: implications for the history of the south-central Capricorn Orogen, Precambrian Res., 90, 119–140, https://doi.org/10.1016/S0301-9268(98)00045-X, 1998.
Portniaguine, O. and Zhdanov, M. S.: 3-D magnetic inversion with data compression and image focusing, Geoophysics, 67, 1532–1541, https://doi.org/10.1190/1.1512749, 2002.
Rittgers, J. B., Revil, A., Mooney, M. A., Karaoulis, M., Wodajo, L., and Hickey, C. J.: Time-lapse joint inversion of geophysical data with automatic joint constraints and dynamic attributes, Geophys. J. Int., 207, 1401–1419, https://doi.org/10.1093/gji/ggw346, 2016.
Schweizer, D., Blum, P., and Butscher, C.: Uncertainty assessment in 3-D geological models of increasing complexity, Solid Earth, 8, 515–530, https://doi.org/10.5194/se-8-515-2017, 2017.
Shannon, C. E. E.: A Mathematical Theory of Communication, Bell Syst. Tech. J., 27, 379–423, https://doi.org/10.1002/j.1538-7305.1948.tb01338.x, 1948.
Sun, J. and Li, Y.: Joint inversion of multiple geophysical data using guided fuzzy c-means clustering, Geophysics, 81, ID37–ID57, https://doi.org/10.1190/geo2015-0457.1, 2016.
Sun, J. and Li, Y.: Joint inversion of multiple geophysical and petrophysical data using generalized fuzzy clustering algorithms, Geophys. J. Int., 208, 1201, https://doi.org/10.1093/gji/ggw442, 2017.
Thiele, S. T., Jessell, M. W., Lindsay, M., Wellmann, J. F., and Pakyuz-Charrier, E.: The topology of geology 2: Topological uncertainty, J. Struct. Geol., 91, 74–87, https://doi.org/10.1016/j.jsg.2016.08.010, 2016.
Tikhonov, A. N. and Arsenin, V. Y.: Solutions of Ill-Posed Problems, John Wiley, New York, 1977.
Vatankhah, S. and Renaut, R. A.: Comment on: `Improving compact gravity inversion based on new weighting functions', by Mohammad Hossein Ghalehnoee, Abdolhamid Ansari and Ahmad Ghorbani, Geophys. J. Int., 211, 346–348, https://doi.org/10.1093/gji/ggx058, 2017.
Wellmann, J. F. and Regenauer-Lieb, K.: Uncertainties have a meaning: Information entropy as a quality measure for 3-D geological models, Tectonophysics, 526–529, 207–216, https://doi.org/10.1016/j.tecto.2011.05.001, 2012.
Wellmann, J. F., Horowitz, F. G., Schill, E., and Regenauer-Lieb, K.: Towards incorporating uncertainty of structural data in 3D geological inversion, Tectonophysics, 490, 141–151, https://doi.org/10.1016/j.tecto.2010.04.022, 2010.
Wellmann, J. F., Lindsay, M., Poh, J., and Jessell, M.: Validating 3-D Structural Models with Geological Knowledge for Improved Uncertainty Evaluations, Energy Procedia, 59, 374–381, https://doi.org/10.1016/j.egypro.2014.10.391, 2014.
Wellmann, J. F., de la Varga, M., Murdie, R. E., Gessner, K., and Jessell, M.: Uncertainty estimation for a geological model of the Sandstone greenstone belt, Western Australia – insights from integrated geological and geophysical inversion in a Bayesian inference framework, Spec. Publ. SP453.12, Geol. Soc., London, https://doi.org/10.1144/SP453.12, 2017.
Wiik, T., Nordskag, J. I., Dischler, E. Ø., and Nguyen, A. K.: Inversion of inline and broadside marine controlled-source electromagnetic data with constraints derived from seismic data, Geophys. Prospect., 63, 1371–1382, https://doi.org/10.1111/1365-2478.12294, 2015.
Williams, N. C.: Geologically-constrained UBC-GIF gravity and magnetic inversions with examples from the Agnew-Wiluna greenstone belt, Western Australia, University of British Columbia, available at: https://open.library.ubc.ca/cIRcle/collections/ubctheses/24/items/1.0052390 (last access: 17 January 2019), 2008.
Williams, N. C.: Mass and magnetic properties for 3D geological and geophysical modelling of the southern Agnew–Wiluna Greenstone Belt and Leinster nickel deposits, Western Australia, Aust. J. Earth Sci., 56, 1111–1142, https://doi.org/10.1080/08120090903246220, 2009.
Yamamoto, J. K., Koike, K., Kikuda, A. T., da Campanha, G. A. C., and Endlen, A.: Post-processing for uncertainty reduction in computed 3D geological models, Tectonophysics, 633, 232–245, https://doi.org/10.1016/j.tecto.2014.07.013, 2014.
Yan, P., Kalscheuer, T., Hedin, P., and Garcia Juanatey, M. A.: Two-dimensional magnetotelluric inversion using reflection seismic data as constraints and application in the COSC project, Geophys. Res. Lett., 44, 3554–3563, https://doi.org/10.1002/2017GL072953, 2017.
Zhdanov, M. S., Gribenko, A., and Wilson, G.: Generalized joint inversion of multimodal geophysical data using Gramian constraints, Geophys. Res. Lett., 39, L09301, https://doi.org/10.1029/2012GL051233, 2012.
- Abstract
- Introduction
- Modelling procedure
- Proof of concept: synthetic case study
- Field validation: Yerrida Basin case study
- Concluding remarks
- Code and data availability
- Appendix A: Data misfit maps from inversion in the Yerrida Basin
- Author contributions
- Competing interests
- Acknowledgements
- References
- Abstract
- Introduction
- Modelling procedure
- Proof of concept: synthetic case study
- Field validation: Yerrida Basin case study
- Concluding remarks
- Code and data availability
- Appendix A: Data misfit maps from inversion in the Yerrida Basin
- Author contributions
- Competing interests
- Acknowledgements
- References