the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Control of increased sedimentation on orogenic fold-and-thrust belt structure – insights into the evolution of the Western Alps
Ritske S. Huismans
Peter van der Beek
We use two-dimensional thermomechanical models to investigate the potential role of rapid filling of foreland basins in the development of orogenic foreland fold-and-thrust belts. We focus on the extensively studied example of the Western European Alps, where a sudden increase in foreland sedimentation rate during the mid-Oligocene is well documented. Our model results indicate that such an increase in sedimentation rate will temporarily disrupt the formation of an otherwise regular, outward-propagating basement thrust-sheet sequence. The frontal basement thrust active at the time of a sudden increase in sedimentation rate remains active for a longer time and accommodates more shortening than the previous thrusts. As the propagation of deformation into the foreland fold-and-thrust belt is strongly connected to basement deformation, this transient phase appears as a period of slow migration of the distal edge of foreland deformation. The predicted pattern of foreland-basin and basement thrust-front propagation is strikingly similar to that observed in the North Alpine Foreland Basin and provides an explanation for the coeval mid-Oligocene filling of the Swiss Molasse Basin, due to increased sediment input from the Alpine orogen, and a marked decrease in thrust-front propagation rate. We also compare our results to predictions from critical-taper theory, and we conclude that they are broadly consistent even though critical-taper theory cannot be used to predict the timing and location of the formation of new basement thrusts when sedimentation is included. The evolution scenario explored here is common in orogenic foreland basins; hence, our results have broad implications for orogenic belts other than the Western Alps.
- Article
(5738 KB) - Full-text XML
-
Supplement
(1311 KB) - BibTeX
- EndNote
The effects of surface processes on orogenic evolution have been intensively studied over the last 3 decades (e.g., Whipple, 2009). Numerous studies have shown that erosion can strongly influence the growth of orogenic hinterland regions, with high erosion rates localizing deformation and creating a lower, narrower orogenic wedge (Beaumont et al., 1992; Braun and Yamato, 2010; Konstantinovskaia and Malavieille, 2005; Koons, 1990; Stolar et al., 2006; Willett, 1999).
Both numerical and analog models also point towards a strong control exerted by syn-orogenic deposition on the structural development of orogenic forelands, as sedimentation rates affect the length of both thin- and thick-skinned foreland thrust sheets, as well as the amount of displacement taken up by individual faults (Adam et al., 2004; Bonnet et al., 2007; Duerto and McClay, 2009; Erdős et al., 2015; Fillon et al., 2012; Malavieille, 2010; Mugnier et al., 1997; Simpson, 2006a, b; Stockmal et al., 2007; Storti and McClay, 1995). In particular, it has been shown experimentally that higher rates of syn-orogenic sedimentation result in longer thin-skinned thrust sheets as well as longer basement thrust sheets under the foreland fold-and-thrust belt (e.g., Erdős et al., 2015; Fillon et al., 2012). However, direct comparison of model predictions with observations from natural case studies (e.g., Fillon et al., 2013) remains scarce.
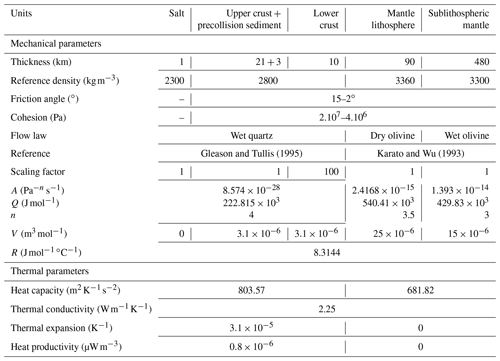
The North Alpine Foreland Basin of France and Switzerland developed in response to continental collision in the Alps during early Tertiary time (Dewey et al., 1973; Homewood et al., 1986; Pfiffner, 1986). The stratigraphic infill of this foreland basin has been well documented (e.g., Sinclair, 1997; Berger et al., 2005; Kuhlemann and Kempf, 2002; Willett and Schlunegger, 2010, and references therein) and consists of two major stages: a Paleocene to mid-Oligocene deep marine (flysch) stage and a mid-Oligocene to late Miocene shallow marine and continental (molasse) stage (Fig. 1).
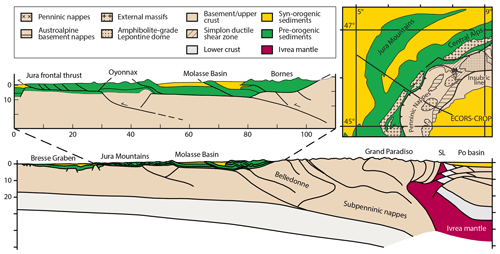
Figure 1Cross section and geological map of the Western Alps, redrawn after Schmid and Kissling (2000) and Schmid et al. (2017), with the inset showing the section interpretation of Roure (2008) along part of the same deep seismic section. SL indicates the location of the Sesia–Lanzo zone.
During the first stage, exhumation rates of the orogenic hinterland and deposition rates in the foreland basin were low; hence, the basin remained underfilled (Allen et al., 1991; Burkhard and Sommaruga, 1998; Sinclair and Allen, 1992). At the onset of the second stage, both erosion rates in the Alps and deposition rates in the foreland basin increased (Schlunegger et al., 1997; Schlunegger and Norton, 2015; Sinclair and Allen, 1992), creating an overfilled foreland basin. The transition from an underfilled to an overfilled state coincided with a marked decrease in thrust-front advance rate (Sinclair and Allen, 1992), but links between the two have remained speculative.
Here, we use numerical models that build on our previous work (Erdős et al., 2015, 2014) to test how an increase in sedimentation rate affects mountain-belt and foreland fold-and-thrust belt evolution. In earlier work (Erdős et al., 2015) we showed how our model predictions were consistent with minimum-work theory. Here, we quantitatively compare our models to critical-taper theory in order to assess the predictions of this simple but widely used theorem, when including a more complex and realistic rheology. Our main aim is to explore the potential causal relationship between a sudden increase in sediment influx and the temporary slowing of thrust-front propagation, as observed in the North Alpine Foreland Basin. Such a sediment accumulation scenario is common in foreland basins (e.g., Allen and Homewood, 1986); hence, the demonstration of a causal relationship should have a significant impact on our understanding of not just the North Alpine Foreland, but also the development of similar orogenic systems around the world.
We explore the potential links between syn-tectonic sedimentation and orogen structure through the use of 2-D arbitrary Lagrangian–Eulerian thermomechanical modeling (Erdős, 2014; Thieulot, 2011) coupled to a simple surface-process algorithm. The numerical experimental setup is very similar to the one used in our previous studies (Erdős et al., 2015, 2014) and is explained in detail in the Supplement.
The thermomechanical model consists of strain-weakening frictional plastic materials that allow for the localization of deformation (e.g., Huismans et al., 2005). Our experiments use a four-layer crust–mantle rheology in which the upper and lower crust as well as the upper lithospheric mantle undergo frictional plastic deformation, while the middle crust and lower lithospheric mantle exhibit power-law viscous creep (Fig. 2). A 3 km thick pre-orogenic sediment package at the top of the model is separated from the crystalline crust by a 1 km thick weak layer representing a décollement horizon (e.g., an evaporite or shale layer). In order to include self-consistent inherited extensional weakness zones, the model is first extended, before the velocity boundary conditions are inverted to create a contractional regime (e.g., Erdős, 2014; Jammes and Huismans, 2012).
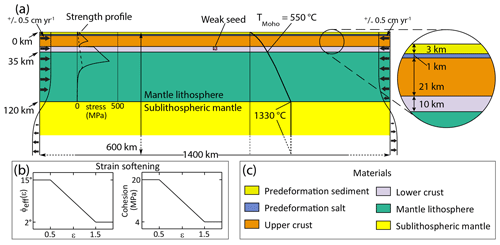
Figure 2(a) Model geometry showing layer thicknesses (including a close-up of the crust), the position and size of the weak seed (pink square), the lateral velocity boundary conditions (black arrows along the sides of the box; note the ± sign), and the initial strength and temperature profiles of the models. The material properties corresponding to each layer (including the syn-tectonic sediments) are presented in Table 1. (b) Frictional plastic strain softening is achieved through a linear decrease in ϕeff from 15 to 2∘ with a simultaneous decrease in C from 20 to 4 MPa. (c) Legend for materials shown in (a).
The surface-process model includes an elevation-dependent erosion algorithm as well as a sedimentation rule that fills topography up to a reference base level at each time step. Both the erosion and sedimentation algorithms are simple and do not conserve mass; however, the resulting basin-fill geometries are consistent with observations from natural foreland-basin systems (DeCelles and Giles, 1996).
The model experiments presented here have sufficiently high resolution (500 m horizontally and 200 m vertically in the upper-crustal domain) to bridge the large range of scales from the entire collisional orogen to the fold-and-thrust belt and the interaction with syn-orogenic deposition.
The initial parameters (crustal setup, convergence velocity) have been chosen to match conditions likely applicable for the Alpine orogenic system. The major difference is that the model does not include seafloor spreading or a lag between breakup and the onset of inversion. The sedimentation–erosion algorithms have been parameterized to represent moderate rates for both processes (see Supplement 1).
We present three model experiments that demonstrate the response of crustal deformation to sudden temporal changes in syn-orogenic sedimentation. For Model 1, neither erosion nor sedimentation is included (Fig. 3a–d). In Model 2, a simple elevation-dependent erosion model is applied together with fixed base-level sedimentation (Erdős et al., 2015): during each model time step, basins are filled with sediments to a prescribed base level (Fig. 3e–g). Model 3 is identical in setup to Model 2, but sedimentation is initiated 10 Myr earlier and the base level of sedimentation is increased during the experiment (15 Myr after initiation) to mimic the transition from an underfilled to an overfilled foreland basin (Fig. 3h–i; see also animations in the Supplement) as observed in the Western Alps (e.g., Sinclair and Allen, 1992).
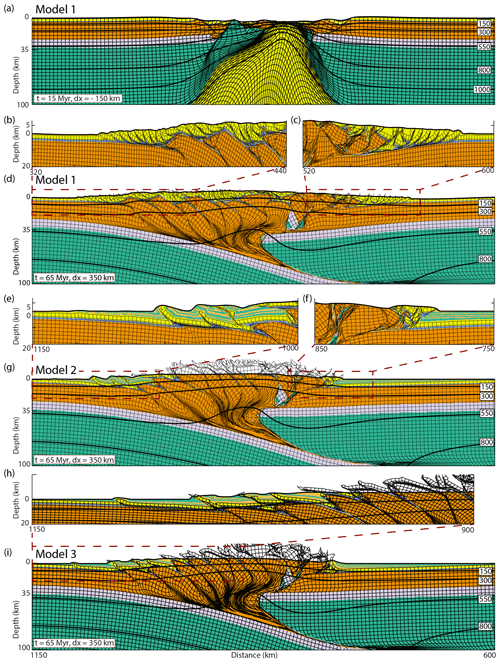
Figure 3Model results. The material coloring scheme is identical to that used in Fig. 2. All models are run for 65 Myr: 15 Myr (150 km) extension followed by 50 Myr (500 km) contraction for a total net contraction of 350 km. The horizontal scale for panels (a), (d), and (g) is the same as that of panel (i). (a–d) Model 1 with no surface processes, showing deformed Lagrangian mesh and isotherms after (a) 15 Myr ( km) and (d) 65 Myr (Δx=350 km). Panels (b) and (c) are extracts from panel (d) showing the small-scale deformation patterns in the foreland fold-and-thrust belts. (e–g) Model 2 including a simple surface-process algorithm filling up accommodation space until a base level of −500 m, showing deformed Lagrangian mesh and isotherms after 65 Myr (Δx=350 km). Panels (e) and (f) are extracts from panel (g) showing the small-scale deformation patterns in the foreland fold-and-thrust belts. (h–i) Model 3 including a simple surface-process algorithm with the sedimentation base level changing from −500 to 0 m at t=45 Myr. Panels show deformed Lagrangian mesh and isotherms after 65 Myr (Δx=350 km). (h) An extract from (i) showing the small-scale deformation patterns in the pro-wedge foreland fold-and-thrust belt. Note that the polarity of subduction is randomly oriented for each model. For ease of comparison we flipped Models 2 and 3 to show them in the orientation that is conventional for the Alpine cross sections.
3.1 Model 1
During the 15 Myr of initial extension, a broad, approximately 200 km wide asymmetric rift basin is formed in the center of the model domain, consisting of a number of rotated crustal blocks with mantle material reaching the surface at two different locations approximately 50 km apart (Fig. 3a). This is followed by a 15 Myr long inversion period culminating in subduction initiation and the formation of an uplifted central block (keystone structure) with a distinct internal structure consisting of a number of inverted normal faults around a core of uplifted lower-crustal and lithospheric mantle material (see Movie 1 in the Supplement).
In the third phase of Model 1, deformation migrates into the subducting plate, building up the pro-wedge (using the terminology as defined by Willett et al., 1993) initially through the formation of a crustal-scale pop-up structure, and then primarily through an outward-propagating sequence of basement thrust sheets (Fig. 3d) with an average thrust-sheet length of 52 km. We use the term basement thrust sheet when referring to thrust sheets that cut the crystalline basement (upper crust). Superposed on this sequence, and often spatially slightly ahead of it, the pre-orogenic sediments are also deformed, creating a complex thin-skinned fold-and-thrust belt (Fig. 3b–c; for an extensive description of the interaction of thin-skinned and thick-skinned deformation, see Erdős et al., 2015). Deformation in the retro-side of the orogen (defined to be the part of the wedge situated on the overriding plate) remains comparatively subdued throughout the model but the initially uplifted central block, which includes a lower-crustal–mantle lithospheric core, is transported more than 50 km onto the overriding plate.
3.2 Model 2, with erosion and sedimentation
The surface-process algorithms in Models 2 and 3 are activated at 45 and 35 Myr (model time), respectively. Consequently, all presented models exhibit the same behavior during the first two phases described above.
Following the initiation of erosion and sedimentation at 45 Myr in Model 2, sediment-loaded foreland basins form on both sides of the orogen, with more intense thin-skinned deformation on the pro-side. The sequence of outward-propagating basement thrust sheets in the pro-wedge is disrupted as deformation remains localized on the active frontal basement thrust for 8 Myr, instead of the 4 Myr observed in Model 1, before stepping out below the foreland basin 13 km farther than in Model 1 (Fig. 3e–g; Movie 2 in the Supplement).
The effect can be well illustrated by comparing the length and displacement of basement thrust sheets around the time of the onset of sedimentation (Fig. 4). Prior to the onset of sedimentation, Thrust A accumulated 6 km of displacement before Thrust B created a new, 45 km long basement thrust sheet (Fig. 4a). After the onset of sedimentation, Thrust B remained active for about 8 Myr and accumulated 24 km of displacement before Thrust C created a new, 83 km long thrust sheet in the footwall of Thrust B (Fig. 4b).
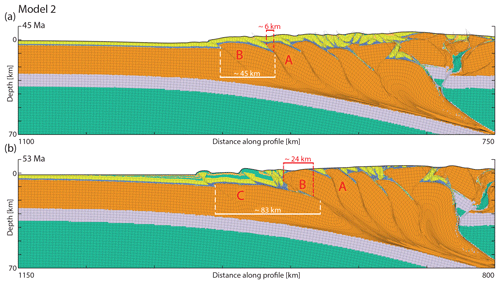
Figure 4The evolution of Model 2 around the time of the onset of sedimentation (and erosion). The material coloring scheme is identical to that used in Fig. 2. (a) Model 2 at 45 Myr (Δx=150 km), just before the onset of sedimentation. White marks show the length of the active external basement thrust sheet (thrusting along Thrust B). The length is measured using the VISU Grid (black grid advected with the materials in the model); we counted the number of undeformed cells in the top row in the basement between the old and the new frontal thrust. Red marks show the amount of displacement along the last abandoned thrust (Thrust A). (b) Model 2 at 53 Myr (Δx=230 km) at the time of the initiation of the first basement thrust sheet after the onset of sedimentation. White marks show the length of the active external basement thrust sheet (thrusting along Thrust C). Red marks show the amount of displacement along the just-abandoned thrust (Thrust B corresponding to Thrust B in Fig. 4a). Further towards the orogenic hinterland the steepened Thrust A is shown (corresponding to Thrust A in Fig. 4a).
As the model progresses further, upper-crustal blocks in the internal parts of the orogen that were initially covered with pre-orogenic sediments are deeply eroded, reaching the surface and bringing the lower-crustal–mantle lithospheric core of the central block to shallow depths. A small sliver of mantle lithospheric material eventually reaches the surface along a back-thrust (Fig. 3f).
We recorded maximum sedimentation rates for 2 Myr intervals (see the alternating orange and green layers of syn-tectonic sediments in Fig. 3e–i) throughout the model. After an initial peak of 2.7 km Myr−1 between 45 and 46 Ma, when the entire available accommodation space is filled up to the prescribed base level, the maximum sedimentation rates in the pro-foreland basin stabilize around an average of 0.45 km Myr−1.
3.3 Model 3, with erosion and intensifying sedimentation
The evolution of Model 3 is very similar to that of Model 2, even though sedimentation and erosion start 10 Myr earlier. Significant differences can only be seen between the pro-foreland basins, after the base level of sedimentation is raised (simulated here by an increase in the sedimentation base level over a 0.5 Myr period) to mimic the transition from an underfilled to an overfilled foreland basin (Fig. 3h–i; Movie 3 in the Supplement). The base-level change results in a temporary (approximately 2 Myr long) increase in the maximum sedimentation rate in the foreland basin (from an average of 0.45 to 1.1 km Myr−1 at the location of the frontal thrust). Subsequently, the maximum sedimentation rate quickly decreases to its previous (average) value.
As observed in Model 2, the initiation of sedimentation alters the architecture of the orogenic foreland by creating longer basement thrust sheets. Similarly, a sudden increase in the sedimentation rate in Model 3 also results in a change in the foreland development. Again, this can be well illustrated by looking at the deformation pattern around the time of increase in sedimentation rate (Fig. 5). Prior to the increase in sedimentation rate, Thrust A accumulated 10 km of displacement before Thrust B created a new, 45 km long basement thrust sheet (Fig. 5a). After the increase in sedimentation rate, Thrust B remained active for about 8 Myr and accumulated 22 km of displacement before Thrust C created a new, 75 km long thrust sheet in the footwall of Thrust B (Fig. 5b).
The subsequent basement thrust-sheet sequence consists of longer thrust sheets (on average 45 km instead of the previous 40 km) that are active for longer times (on average 6.5 instead of 4 Myr) compared with the model behavior before the increase in sedimentation rate (Fig. 3h–i; Movie 3 in the Supplement).
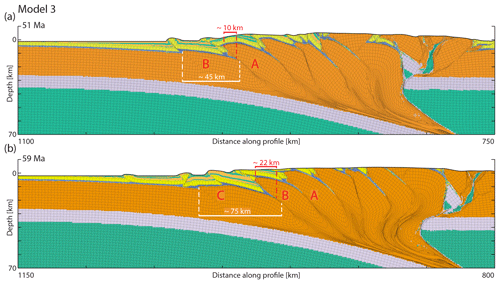
Figure 5The evolution of Model 3 around the time of increase in sedimentation rate. The material coloring scheme is identical to that used in Fig. 2. (a) Model 3 at 51 Myr (Δx=210 km), the time of increase in sedimentation rate. White marks show the length of the active external basement thrust sheet (thrusting along Thrust B). The length calculation method is the same as in Fig. 4. Red marks show the amount of displacement along the last abandoned thrust (Thrust A). (b) Model 3 at 59 Myr (Δx=290 km) at the time of the initiation of the first basement thrust sheet after the increase in sedimentation rate. White marks show the length of the active external basement thrust sheet (thrusting along Thrust C). Red marks show the amount of displacement along the just-abandoned thrust (Thrust B corresponding to Thrust B in a). Further towards the orogenic hinterlands the steepening Thrust A is shown (corresponding to Thrust A in a).
We attempt to explain the observed behavior of our models at the scale of the entire wedge in terms of critical-taper theory (Chapple, 1978; Dahlen, 1990; Davis et al., 1983). According to this theory, a wedge will evolve towards a critical state characterized by being at the verge of brittle failure both internally and at its base. As a consequence, equilibrium is reflected by a self-similarly growing wedge with a stable surface slope (α) and detachment dip (β) (Davis et al., 1983); such a wedge should react instantaneously to changes in stress regime. Lateral variations in the structure and surface slope of European Alpine foreland have been explained using critical-taper theory (von Hagke et al., 2014, and references therein). However, this purely brittle continuum-mechanical theory has limited applicability to our model due to the presence of viscous plastic deformation and strain-weakening materials (Buiter, 2012; Simpson, 2011). Simpson (2011) argued that an elastic–plastic wedge is often well below the critical stress threshold locally. Hence, we explore here whether the large-scale deformation of our model orogens exhibits a behavior that is consistent with critical-taper theory predictions.
When we consider a brittle Coulomb wedge, a sudden increase in sedimentation rate will result in the filling up of the previously unfilled (or underfilled) foreland basin, reducing α significantly while moderately increasing β due to the loading of the basin. Critical-taper theory predicts that such a sudden change in the taper angles, without a simultaneous modification of the mechanical properties of the wedge or the basal detachment, should drive the wedge towards a subcritical state. Subsequently, the wedge needs to deform (thicken) internally to increase its taper angle until it reaches critical state once again (see also Willett and Schlunegger, 2010).
We analyze five models to assess whether our pro-wedges replicate the above predictions of critical-taper theory. In order to isolate the potentially tangled effects of erosion and sedimentation, we include in this analysis a model with erosion but no sedimentation (Model 1.1) and one with sedimentation but no erosion (Model 2.1). We define the wedge as the zone between the surface trace of the frontal (thin-skinned) thrust and the lower-crustal indenter of the overriding plate (denoted S point in Fig. 6). The basal slope β is calculated using the top of the lower crust as a reference horizon. We acknowledge that these definitions are arbitrary and in some cases at odds with assumptions of critical-taper theory (i.e., the top of the lower crust separates the ductile middle crust and the brittle lower crust), but these definitions allow for a consistent derivation of α and β values for each time slice in every model.
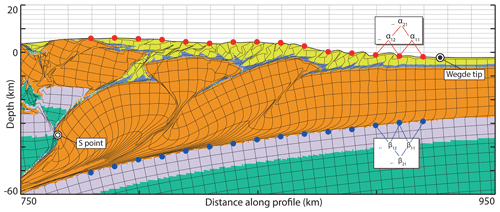
Figure 6Example of α and β sampling routine. S point: internal limit of the wedge considered for critical-taper analysis, located at the tip of the lower-crustal indenter of the overriding plate. Wedge tip: the outer tip of the wedge considered for critical-taper analysis, located at the tip of the orogenic deformation zone. Red dots: elevation sampling points along the wedge for a given sampling interval. For each sampling interval, α is first calculated for every adjacent point (e.g., α11, α12) before we calculate the mean (α1) of these local, individual α values for the entire wedge. The process is then repeated for all sampling intervals (e.g., α21). Blue dots: depth sampling points along the wedge for a given sampling interval. β is calculated in the same manner as α (described above).
Due to the complexity of the surface topography (and to a lesser extent the basal décollement), representing the entire wedge with a single α–β pair is notoriously difficult. In this study, we calculated multiple sets of α and β values along the wedge using a range of different sampling intervals for every time slice of the model (e.g., Fig. 6). Subsequently we calculated the mean α and β values for each sampling interval and visualized the resulting mean of these sampling intervals using box plots (see Fig. 7). This analysis allows us to identify temporal trends that are persistent through a range of characteristic length scales. We tested over 100 different sampling intervals from 2.5 to 100 km and decided to use a subset of 41 of these, ranging from 10 to 30 km, to create the plots for this study. Note that the trends described here were also present at the higher and lower ends of the sampling scale.
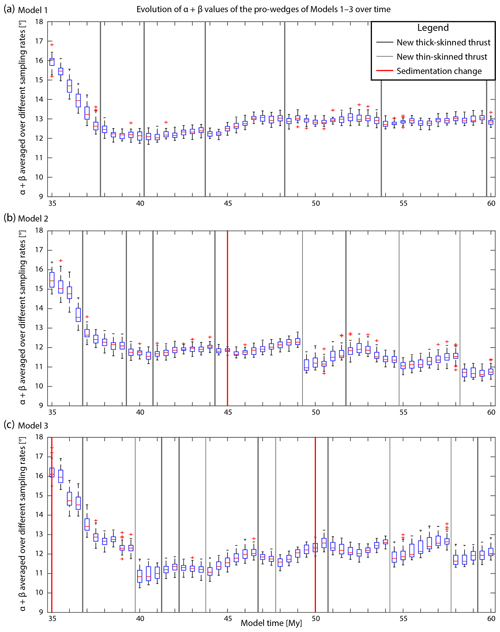
Figure 7Plots of α+β vs. model time for Models 1 (a), 2 (b), and 3 (c). For each time slice, the α and β values were determined using a range of sampling intervals. The box plots present the average α+β, α, and β values of these individual sampling intervals calculated for the entire wedge. On each box, the central mark is the median, the edges of the box are the 25th and 75th percentiles, and the whiskers extend to the most extreme data points considered not to be outliers. The outliers are plotted individually.
For brevity, we only discuss the implications of the above detailed critical-taper analysis. The individual α, β, and α+β vs. model time plots and their detailed interpretations can be found in the Supplement, along with a detailed description of Models 1.1 and 2.1. Generally, the models without sedimentation conform to the predictions of critical-taper theory. After an initial mountain-building phase, α+β stabilizes at a roughly stable level and is only slightly perturbed around individual basement thrusting events (see Fig. 7a). Erosion slightly increases α and reduces β, keeping α+β at a constant value. The increase in α is a result of the development of a narrower and steeper wedge with a narrower foreland basin. Conversely, the decrease in β is partly due to decreased topographic loading: models with erosion do not produce topography higher than 6 km, while models without erosion can grow topography as high as 8 km.
When sedimentation is included in the models, the behavior is considerably more complex and the importance of the initiation of new thin-skinned frontal thrusts becomes more pronounced (Fig. 7b and c). As the orogenic foreland – and hence the wedge itself – grows wider, the crustal load exerted by the orogen grows as well. The loading increases β until the deformation moves to a new frontal thrust, further widening the wedge and incorporating a previously undeformed, gently dipping basement, which instantaneously reduces β. These cycles in β are superimposed on top of a long-term decreasing trend, likely resulting from the wedge becoming larger, warmer, and easier to deform over time. In the meantime, the wide and low-relief orogenic foreland thrust belts generally decrease α to very low (0.5–2∘) values.
The observed cyclic behavior, in which the deformation periodically migrates to a new frontal thrust, is similar to the “punctuated thrust deformation” described by Hoth et al. (2007) and Naylor and Sinclair (2007), whereby the position of the deformation front fluctuates as successive thrusts are gradually incorporated into the wedge. This discrete, punctuated behavior causes the wedge to oscillate around a critical-taper value rather than staying in complete equilibrium through time. Here we have shown, moreover, how erosion and sedimentation influence this behavior consistent with the predictions of critical-taper theory.
We have created animations showing the temporal and spatial (along-profile) variations of α, β, an arbitrary metric of the shallow strain rate, and the topography for Models 1 and 2 (see Movies 6 to 9 in the Supplement). Our aim with this exercise was to establish whether the changes in topography (α, β) are driven by strain-rate changes or the other way around. A key observation here is that the evolution of α in Model 1 (and to a lesser extent in Model 2) shows a particular pattern: a new thrust is activated after α of the region around the active fault reaches ∼10∘. After the new thrust is activated, this high α rapidly decays. This suggests that α ≈10∘ can locally be seen as a critical value, which triggers the formation of a new frontal thrust. This new thrust is generally activated close to the tip of the active thin-skinned deformation front.
When sedimentation is included (Model 2), the high-α regions are more persistent. We argue that, since the sediments are stifling the foreland basin, there is significantly less room for thin-skinned deformation that would otherwise create a gentler slope around the surface trace of the basement thrusts. This results in negative-α basins sliding between thick-skinned thrusts on top of the décollement. Our thermomechanical models are therefore in agreement with the analytical results shown by Willett and Schlunegger (2010).
The first-order evolution of all three presented models is similar, regardless of the imposed erosion–sedimentation scenario. First, an asymmetric rift is formed with a wider and a narrower passive margin consisting of rotated upper-crustal fault blocks on either side of an upwelling sublithospheric mantle. This rifting phase is followed immediately by the inversion of the large normal faults. After full inversion, a central keystone structure is uplifted, with a crustal-scale thrust on either side of it. As the rift was asymmetric, the keystone structure and its base are also asymmetric. The subduction interface is consistently formed in the basement of the initially wider passive margin. After the polarity of subduction is established, a new basement thrust is formed in the subducting pro-wedge lithosphere on average every 3.1 Myr (in the case of Model 1) in an outward-propagating sequence. As the initial model setup is completely symmetrical, the orientation of the initial asymmetric rift and, through that, the polarity of the subduction are decided randomly. The main differences between the models are the position and timing of thrust activations.
The step-like migration of the deformation front and, to a lesser extent, the distal edge of the foreland are present throughout all our model experiments, but are enhanced when a change in the sedimentation history occurs. In Model 2, the distal edge of the foreland basin advances rapidly after the onset of sedimentation, while the basement deformation front remains stationary (Fig. 8b). After this transitional period, lasting about 2 Myr, a new propagation order is established with longer basement thrust sheets (on average 46 instead of 40 km) that stay active for longer times (on average 7 instead of 4.5 Myr). In Model 3, two such transitional periods can be observed (Fig. 8c): one at the onset of sedimentation (35 Ma; see caption) and one at the increase in sedimentation rate (20 Ma; see caption). During this latter transition, the distal edge of the foreland basin rapidly advances again (approximately 150 km in 2.5 Myr), while the outermost basement thrust remains active for 4 Myr longer than the previous frontal thrusts (7.5 Myr instead of the previous 3.5 Myr).
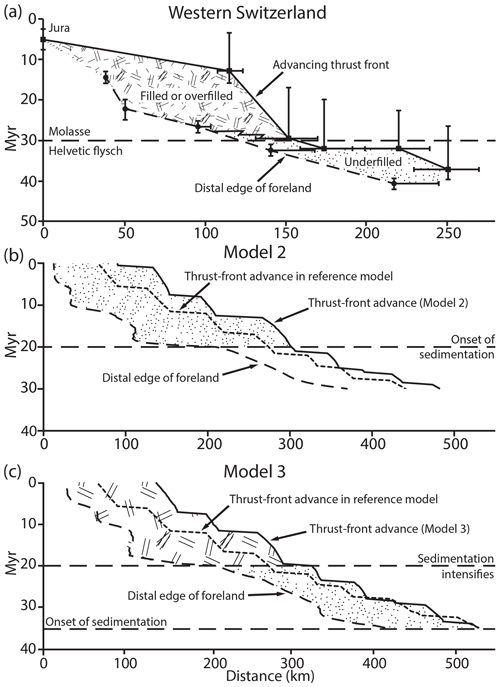
Figure 8Thrust-front propagation and sediment onlap on the distal edge of the foreland basin vs. time (a) in the Western Alps (redrawn after Sinclair, 1997) (b) derived from Model 2 and (c) derived from Model 3. The thin dashed line in (b) and (c) shows the thrust-front propagation pattern of Model 1. Note that in (b) and (c) the time axis of the models is reversed from Myr (forward model time) to Ma (time before “present”) to fit the original axis of the Western Alps.
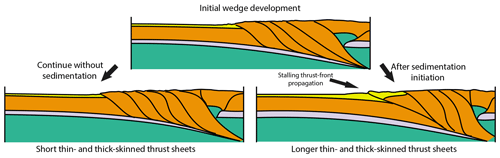
Figure 9Conceptual figure showing the difference between the evolution of a mountain belt with and without intensive late-stage sedimentation. The cartoons are generalizations of our model results, depicting them after the same amount of convergence.
In general, the location of a newly initiated in-sequence basement thrust corresponds to the point at which the total work needed to slide on the viscous mid-crustal weak zone and to break through the upper crust is lower than the work needed to maintain deformation on the existing thrust front (Erdős et al., 2015; Fillon et al., 2012; Hardy et al., 1998). Upon initiation (or increase) of sedimentation in the foreland basin, the work required to create a new basement thrust is suddenly increased as the sediments effectively expand the thickness of the rock column overlying the mid-crustal weak zone (Erdős et al., 2015). This increased resistance against the formation of a new basement thrust breaks the previous cyclic behavior and delays the propagation of the basement deformation front into the foreland basin.
5.1 Comparison with the Alps
The models presented here capture a number of first-order features of the Western European Alps (Schmid and Kissling, 2000; Schmid et al., 2017) (Fig. 1), including the following: (a) a major step in Moho depth between the European and Adriatic (or Apulian) plates; (b) strong decoupling between the upper and lower crust, with the lower crust under-thrusting and subducting with the mantle lithosphere; (c) stacking of basement thrust sheets in the central part of the orogen; (d) shallow emplacement of lithospheric mantle material in the retro-wedge, with a sliver of mantle material reaching the surface (Fig. 3f, g, i), loosely resembling the Ivrea body and Sesia–Lanzo zone, respectively; and (e) a generally asymmetric orogen with deformation stepping out much further on the pro-side than on the retro-side. The presence of a weak décollement below the pre-orogenic succession in this model is also characteristic of the western Alpine foreland and allows for the coexistence of thin-skinned and thick-skinned tectonics (see, e.g., Erdős et al., 2015), a feature that is much less prominent in the Eastern Alps, where the décollement is absent (Schmid et al., 2004).
The initial extensional phase allows for the creation of physically self-consistent inherited structural weakness zones, as observed in most orogens. After extending the model for 15 Myr, the continental lithosphere has effectively ruptured, creating two small separate ocean basins that mimic the pre-orogenic presence of the Piemont–Ligurian and Valais basins in the Alpine domain (Stampfli et al., 2001). It must be pointed out that running the models further in extensional mode in this setup is not viable because there is no built-in mechanism for the creation of oceanic lithosphere. The effects of a thermal relaxation phase were not explored either, as potentially important mechanisms like strain healing are not yet implemented in the model.
The basement under the pro-foreland basin is rather smooth, dipping on average 3∘ towards the orogen at the time slice captured in Fig. 4b (which corresponds best to the present state of the North Alpine Foreland Basin). This value is in good agreement with those inferred from the interpretation of seismic reflection lines (Burkhard and Sommaruga, 1998; Sommaruga, 1999).
The increase in sedimentation in Models 2 and 3 links basement thrust-front propagation and the onlap of sediments onto the foreland, as observed in the North Alpine Foreland Basin (e.g., Sinclair, 1997; Fig. 5). Both deposition scenarios lead to longer frontal basement thrusts that remain active for a longer period before a new basement thrust is formed. This suggests that increased sedimentation, which resulted from the increasing relief and changing climate in the Alpine hinterland (Schlunegger et al., 1997; Schlunegger and Norton, 2015), was a significant factor in the mid-Oligocene stalling of thrust-front advance observed in the western section of the North Alpine Foreland. Note that this behavior is not observed further east along the foreland where the amount of orogen-perpendicular shortening is less and the decoupling salt layer is absent from the foreland basin (Schmid et al., 2004). This could well limit the distance to which the thin-skinned deformation of the foreland fold-and-thrust belt can reach.
The shortening rates, timing of orogenesis, and transition from an underfilled to an overfilled basin in the case of Model 3 are based on observations in the northern foreland of the Western Alps. The timescales of thrust and basin evolution of the models are comparable to those of the western Alpine system. The jump in thrust-front position is of the order of 100 km both in the model and nature, but the stagnation in the Alps lasted about twice as long as observed in the models.
We also note that the stepwise behavior shown by Sinclair (1997) is present in our models even if there is no change in the deposition scenario applied. However, we argue that an increase in the amount of material deposited in the foreland basin will necessary result in stalling of the basement thrust-front propagation, while it will also allow for the distal edge of the foreland basin to migrate further onto the downgoing plate.
5.2 Implications for other mountain belts
An early synthetic stratigraphic model of foreland-basin development (Flemings and Jordan, 1989) showed that peripheral orogenic foreland basins have a tendency to evolve from an underfilled into an overfilled state. Numerous studies focusing on the stratigraphic infill of natural foreland basins (e.g., Allen et al., 1991; DeCelles and Burden, 1992; Quinlan and Beaumont, 1984) have demonstrated the merits of this model. Moreover, as the internal part of the orogen grows, more surface area reaches higher elevations, resulting in a potential increase in erosion rates and, consequently, sediment flux into the foreland basin (Simpson, 2006a, b; Sinclair et al., 2005). Hence, the orogenic foreland-basin evolution scenario described in this study should be applicable to a wide range of orogens around the globe. A prime example may be the southern Pyrenean (pro-)foreland fold-and-thrust belt, where a middle Eocene increase in sedimentation rate was accompanied by stalling of the thrust front (Sinclair et al., 2005). Based on their stratigraphic models, Flemings and Jordan (1989) proposed that changes in the rate of thrust loading, climate, or source-rock lithology (all present in their models through surface-process transport coefficients) can cause the shift from underfilled to overfilled basins. Our model results imply that there is a strong feedback between these potential controls and the state of the basin fill.
The thermomechanical models presented here provide first-order insights into the intricate relationship between changing sedimentation rates and deformation patterns in orogenic forelands (Fig. 9). Our models show that a sudden increase in sedimentation rate disrupts thrust-front and foreland-basin propagation patterns. The outermost basement thrust remains active for a significantly longer time and accumulates more deformation than previous thrusts developed during periods of lower sediment input, before deformation steps out again under the sediment-loaded foreland basin. After determining α and β values for each model and examining their evolution over time, we conclude that they are broadly consistent with predictions from critical-taper theory, despite the more complex and realistic rheology included in our models. However, when sedimentation is included, critical-taper theory cannot be used to predict the timing and location of the formation of new basement thrusts.
The results are in good agreement with observations from the Western Alps and the North Alpine Foreland Basin, where deformation remained relatively stable for an extended period of time after the foreland basin shifted from an underfilled to a filled–overfilled state. They should also be applicable to other orogens around the globe.
The data sets for this article are available as video supplements in the Supplement and via the following DOIs: evolution of Model 1 (https://doi.org/10.5446/38571; Erdős et al., 2018a); evolution of Model 2 (https://doi.org/10.5446/38572; Erdős et al., 2018b); evolution of Model 3 (https://doi.org/10.5446/38576; Erdős et al., 2018c); evolution of Model 1.1 (https://doi.org/10.5446/38573; Erdős et al., 2018d); evolution of Model 2.1 (https://doi.org/10.5446/38574; Erdős et al., 2018e); α, shallow strain rate, and topographic evolution of Model 1 (https://doi.org/10.5446/38575; Erdős et al., 2018f); β, shallow strain rate, and topographic evolution of Model 1 (https://doi.org/10.5446/38578; Erdős et al., 2018h); α, shallow strain rate, and topographic evolution of Model 2 (https://doi.org/10.5446/38577; Erdős et al., 2018g); β, shallow strain rate, and topographic evolution of Model 2 (https://doi.org/10.5446/38579; Erdős et al., 2018i).
The supplement related to this article is available online at: https://doi.org/10.5194/se-10-391-2019-supplement.
ZE and RSH designed the experimental setup. ZE ran the model experiments and all three authors contributed to the interpretation of the results. ZE prepared the paper with contributions from both coauthors.
The authors declare that they have no conflict of interest.
We thank Fritz Schlunegger for his constructive comments at an early stage of this project and Stefan Schmid for providing the latest version of the Alpine cross section assembled by his group. We also thank Mary Ford and Christoph von Hagke for their constructive feedback on a previous version of this paper.
This paper was edited by Bernhard Grasemann and reviewed by Xiaodong Yang and one anonymous referee.
Adam, J., Klaeschen, D., Kukowski, N., and Flueh, E.: Upward delamination of Cascadia Basin sediment infill with landward frontal accretion thrusting caused by rapid glacial age material flux, Tectonics, 23, TC3009, https://doi.org/10.1029/2002TC001475, 2004.
Allen, P. A. and Homewood, P.: Foreland Basins, International Association of Sedimentologists, Special Publication no. 8, Blackwell Scientific Publications, Oxford, 1986.
Allen, P. A., Crampton, S. L., and Sinclair, H. D.: The inception and early evolution of the North Alpine Foreland Basin, Switzerland, Basin Res., 3, 143–163, https://doi.org/10.1111/j.1365-2117.1991.tb00124.x, 1991.
Beaumont, C., Fullsack, P., and Hamilton, J.: Erosional control of active compressional orogens, in: Thrust Tectonics, edited by: McClay, K. R., Chapman & Hall, London, 1–18, 1992.
Berger, J.-P., Reichenbacher, B., Becker, D., Grimm, M., Grimm, K., Picot, L., Storni, A., Pirkenseer, C., and Schaefer, A.: Eocene-Pliocene time scale and stratigraphy of the Upper Rhine Graben (URG) and the Swiss Molasse Basin (SMB), Int. J. Earth Sci., 94, 711–731, 2005.
Bonnet, C., Malavieille, J., and Mosar, J.: Interactions between tectonics, erosion, and sedimentation during the recent evolution of the Alpine orogen: Analogue modeling insights, Tectonics, 26, TC6016, https://doi.org/10.1029/2006tc002048, 2007.
Braun, J. and Yamato, P.: Structural evolution of a three-dimensional, finite-width crustal wedge, Tectonophysics, 484, 181–192, https://doi.org/10.1016/j.tecto.2009.08.032, 2010.
Buiter, S. J. H.: A review of brittle compressional wedge models, Tectonophysics, 530–531, 1–17, https://doi.org/10.1016/j.tecto.2011.12.018, 2012.
Burkhard, M. and Sommaruga, A.: Evolution of the western Swiss Molasse basin: structural relations with the Alps and the Jura belt, Geological Society, London, Special Publications, 134, 279–298, 1998.
Chapple, W. M.: Mechanics of thin-skinned fold-and-thrust belts, Geol. Soc. Am. Bull., 89, 1189–1198, 1978.
Dahlen, F. A.: Critical taper model of fold-and-thrust belts and accretionary wedges, Annu. Rev. Earth Pl. Sc., 18, 55–99, 1990.
Davis, D., Suppe, J., and Dahlen, F. A.: Mechanics of fold-and-thrust belts and accretionary wedges, J. Geophys. Res., 88, 1153–1172, 1983.
DeCelles, P. and Burden, E. T.: Non-marine sedimentation in the overfilled part of the Jurassic-Cretaceous Cordilleran foreland basin: Morrison and Cloverly Formations, central Wyoming, USA, Basin Res., 4, 291–313, 1992.
DeCelles, P. G. and Giles, K. A.: Foreland basin systems, Basin Res., 8, 105–123, 1996.
Dewey, J. F., Pitman, W. C., Ryan, W. B. F., and Bonnin, J.: Plate tectonics and the evolution of the Alpine system, Geol. Soc. Am. Bull., 84, 3137–3180, 1973.
Duerto, L. and McClay, K.: The role of syntectonic sedimentation in the evolution of doubly vergent thrust wedges and foreland folds, Mar. Petrol. Geol., 26, 1051–1069, https://doi.org/10.1016/j.marpetgeo.2008.07.004, 2009.
Erdős, Z.: Coupled surface process and tectonic modelling of extension-inversion tectonics in the Pyrenees, PhD Thesis, University of Bergen, Norway, ISBN 978-82-308-2829-8, 2014.
Erdős, Z., Huismans, R. S., van der Beek, P., and Thieulot, C.: Extensional inheritance and surface processes as controlling factors of mountain belt structure, J. Geophys. Res.-Sol. Ea., 119, 9042–9061, https://doi.org/10.1002/2014jb011408, 2014.
Erdős, Z., Huismans, R. S., and van der Beek, P.: First-order control of syntectonic sedimentation on crustal-scale structure of mountain belts, J. Geophys. Res.-Sol. Ea., 120, 5362–5377, https://doi.org/10.1002/2014jb011785, 2015.
Erdős, Z., Huismans, R. S., and van der Beek, P.: Evolution of Model 1, https://doi.org/10.5446/38571, 2018a.
Erdős, Z., Huismans, R. S., and van der Beek, P.: Evolution of Model 2, https://doi.org/10.5446/38572, 2018b.
Erdős, Z., Huismans, R. S., and van der Beek, P.: Evolution of Model 3, https://doi.org/10.5446/38576, 2018c.
Erdős, Z., Huismans, R. S., and van der Beek, P.: Evolution of Model 1.1, https://doi.org/10.5446/38573, 2018d.
Erdős, Z., Huismans, R. S., and van der Beek, P.: Evolution of Model 2.1, https://doi.org/10.5446/38574, 2018e.
Erdős, Z., Huismans, R. S., and van der Beek, P.: Model 1: α-Topography-Strain rate, https://doi.org/10.5446/38575, 2018f.
Erdős, Z., Huismans, R. S., and van der Beek, P.: Model 2: α-Topography-Strain rate, https://doi.org/10.5446/38577, 2018g.
Erdős, Z., Huismans, R. S., and van der Beek, P.: Model 1: β-Topography-Strain rate, https://doi.org/10.5446/38578, 2018h.
Erdős, Z., Huismans, R. S., and van der Beek, P.: Model 2: β-Topography-Strain rate, https://doi.org/10.5446/38579, 2018i.
Fillon, C., Huismans, R. S., and van der Beek, P.: Syntectonic sedimentation effects on the growth of fold-and-thrust belts, Geology, 41, 83–86, https://doi.org/10.1130/g33531.1, 2012.
Fillon, C., Huismans, R. S., van der Beek, P., and Muñoz, J. A.: Syntectonic sedimentation controls on the evolution of the southern Pyrenean fold-and-thrust belt: Inferences from coupled tectonic-surface processes models, J. Geophys. Res.-Sol. Ea., 118, 5665–5680, https://doi.org/10.1002/jgrb.50368, 2013.
Flemings, P. B. and Jordan, T. E.: A synthetic stratigraphic model of foreland basin development, J. Geophys. Res., 94, 3851–3866, 1989.
Gleason, G. C. and Tullis, J.: A Flow Law for Dislocation Creep of Quartz Aggregates Determined with the Molten-Salt Cell, Tectonophysics, 247, 1–23, 1995.
Hardy, S., Duncan, C., Masek, J., and Brown, D.: Minimum work, fault activity and the growth of critical wedges in fold and thrust belts, Basin Res., 10, 365–373, 1998.
Homewood, P., Allen, P. A., and Williams, G. D.: Dynamics of the Molasse Basin of western Switzerland, Int. As. Sed., 8, 199–217, 1986.
Hoth, S., Hoffmann-Rothe, A., and Kukowski, N.: Frontal accretion: An internal clock for bivergent wedge deformation and surface uplift, J. Geophys. Res., 112, B06408, https://doi.org/10.1029/2006jb004357, 2007.
Huismans, R. S., Buiter, S. J. H., and Beaumont, C.: Effect of plastic-viscous layering and strain softening on mode selection during lithospheric extension, J. Geophys. Res., 110, B02406, https://doi.org/10.1029/2004jb003114, 2005.
Jammes, S. and Huismans, R. S.: Structural styles of mountain building: Controls of lithospheric rheologic stratification and extensional inheritance, J. Geophys. Res., 111, B10403, https://doi.org/10.1029/2012jb009376, 2012.
Karato, S. and Wu, P.: Rheology of the upper mantle: a synthesis, Science, 260, 771–778, 1993.
Konstantinovskaia, E. and Malavieille, J.: Erosion and exhumation in accretionary orogens: Experimental and geological approaches, Geochem. Geophys. Geosyst., 6, Q02006, https://doi.org/10.1029/2004gc000794, 2005.
Koons, P. O.: Two-sided orogen: Collision and erosion from the sand box to the Southern Alps, New Zealand, Geology, 18, 679–682, 1990.
Kuhlemann, J. and Kempf, O.: Post-Eocene evolution of the North Alpine Foreland Basin and its response to Alpine tectonics, Sediment. Geol., 152, 45–78, https://doi.org/10.1016/S0037-0738(01)00285-8, 2002.
Malavieille, J.: Impact of erosion, sedimentation, and structural heritage on the structure and kinematics of orogenic wedges: Analog models and case studies, GSA Today, 20, 4–10, https://doi.org/10.1130/gsatg48a.1, 2010.
Mugnier, J. L., Baby, P., Colletta, B., Vinour, P., Bale, P., and Leturmy, P.: Thrust geometry controlled by erosion and sedimentation: A view from analogue models, Geology, 25, 427–430, 1997.
Naylor, M. and Sinclair, H. D.: Punctuated thrust deformation in the context of doubly vergent thrust wedges: Implications for the localization of uplift and exhumation, Geology, 35, 559–562, 2007.
Pfiffner, O. A.: Evolution of the north Alpine foreland basin in the Central Alps, Int. As. Sed., 8, 219–228, 1986.
Quinlan, G. M. and Beaumont, C.: Appalachian thrusting, lithospheric flexure, and the Paleozoic stratigraphy of the Eastern Interior of North America, Can. J. Earth Sci., 21, 973–996, 1984.
Roure, F.: Foreland and Hinterland basins: what controls their evolution?, Swiss J. Geosci., 101, 5–29, https://doi.org/10.1007/s00015-008-1285-x, 2008.
Schlunegger, F. and Norton, K. P.: Climate vs. tectonics: the competing roles of Late Oligocene warming and Alpine orogenesis in constructing alluvial megafan sequences in the North Alpine foreland basin, Basin Res., 27, 230–245, https://doi.org/10.1111/bre.12070, 2015.
Schlunegger, F., Jordan, T. E., and Klaper, E. M.: Controls of erosional denudation in the orogen on foreland basin evolution: The Oligocene central Swiss Molasse Basin as an example, Tectonics, 16, 823–840, 1997.
Schmid, S. M. and Kissling, E.: The arc of the western Alps in the light of geophysical data on deep crustal structure, Tectonics, 19, 62–85, https://doi.org/10.1029/1999tc900057, 2000.
Schmid, S. M., Fugenschuh, B., Kissling, E., and Schuster, R.: Tectonic map and overall architecture of the Alpine orogen, Eclogae Geol. Helv., 97, 93–117, https://doi.org/10.1007/s00015-004-1113-x, 2004.
Schmid, S. M., Kissling, E., Diehl, T., van Hinsbergen, D. J. J., and Molli, G.: Ivrea mantle wedge, arc of the Western Alps, and kinematic evolution of the Alps–Apennines orogenic system, Swiss J. Geosci., 110, 581–612, https://doi.org/10.1007/s00015-016-0237-0, 2017.
Simpson, G. D. H.: How and to what extent does the emergence of orogens above sea level influence their tectonic development?, Terra Nova, 18, 447–451, https://doi.org/10.1111/j.1365-3121.2006.00711.x, 2006a.
Simpson, G. D. H.: Modelling interactions between fold-thrust belt deformation, foreland flexure and surface mass transport, Basin Res., 18, 125–143, https://doi.org/10.1111/j.1365-2117.2006.00287.x, 2006b.
Simpson, G. D. H.: Mechanics of non-critical fold–thrust belts based on finite element models, Tectonophysics, 499, 142–155, https://doi.org/10.1016/j.tecto.2011.01.004, 2011.
Sinclair, H. D.: Tectonostratigraphic model for underfilled peripheral foreland basins: An Alpine perspective, Geol. Soc. Am. Bull., 109, 324–346, 1997.
Sinclair, H. D. and Allen, P. A.: Vertical versus horizontal motions in the Alpine orogenic wedge: stratigraphic response in the foreland basin, Basin Res., 4, 215–232, 1992.
Sinclair, H. D., Gibson, M., Naylor, M., and Morris, R. G.: Asymmetric growth of the Pyrenees revealed through measurement and modeling of orogenic fluxes, Am. J. Sci., 305, 369–406, https://doi.org/10.2475/ajs.305.5.369, 2005.
Sommaruga, A.: Decollement tectonics in the Jura foreland fold-and-thrust belt, Mar. Petrol. Geol., 16, 111–134, https://doi.org/10.1016/S0264-8172(98)00068-3, 1999.
Stampfli, G., Mosar, J., Favre, P., Pillevuit, A., and Vannay, J. C.: Permo-Mesozoic evolution of the western Tethys realm: the Neo-Tethys East Mediterranean Basin connection, in: Peri-Tethys Memoir 6: Peri-Tethyan Rift/Wrench Basins and Passive Margins, edited by: Ziegler, P. A., Mémoire du Musée National d'Histoire Naturelle, Paris, 51–108, 2001.
Stockmal, G. S., Beaumont, C., Nguyen, M., and Lee, B.: Mechanics of thin-skinned fold-and-thrust belts: Insights from numerical models, Geol. S. Am. S., 433, 63–98, https://doi.org/10.1130/2007.2433(04), 2007.
Stolar, D. B., Willett, S. D., and Roe, G. H.: Climatic and tectonic forcing of a critical orogen, Geol. S. Am. S., 398, 241–250, https://doi.org/10.1130/2006.2398(14), 2006.
Storti, F. and McClay, K.: Influence of syntectonic sedimentation on thrust wedges in analog models, Geology, 23, 999–1002, 1995.
Thieulot, C.: FANTOM: Two- and three-dimensional numerical modelling of creeping flows for the solution of geological problems. Phys. Earth Planet. In., 188, 47–68, https://doi.org/10.1016/j.pepi.2011.06.011, 2011.
von Hagke, C., Oncken, O., and Evseev, S.: Critical taper analysis reveals lithological control of variations in detachment strength: An analysis of the Alpine basal detachment (Swiss Alps), Geochem. Geophys. Geosyst., 15, 176–191, https://doi.org/10.1002/2013gc005018, 2014.
Whipple, K. X.: The influence of climate on the tectonic evolution of mountain belts, Nat. Geosci., 2, 97–104, https://doi.org/10.1038/ngeo413, 2009.
Willett, S. D.: Orogeny and orography: The effects of erosion on the structure of mountain belts, J. Geophys. Res., 104, 28957–28981, 1999.
Willett, S. D. and Schlunegger, F.: The last phase of deposition in the Swiss Molasse Basin: from foredeep to negative-alpha basin, Basin Res., 22, 623–639, https://doi.org/10.1111/j.1365-2117.2009.00435.x, 2010.
Willett, S., Beaumont, C., and Fullsack, P.: Mechanical model for the tectonics of doubly vergent compressional orogens, Geology, 21, 371–374, 1993.