the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
ER3D: a structural and geophysical 3-D model of central Emilia-Romagna (northern Italy) for numerical simulation of earthquake ground motion
Giovanna Laurenzano
Maria Adelaide Romano
Enrico Priolo
Luca Martelli
During the 2012 seismic sequence of the Emilia region (northern Italy), the earthquake ground motion in the epicentral area featured longer duration and higher velocity than those estimated by empirical-based prediction equations typically adopted in Italy. In order to explain these anomalies, we (1) build up a structural and geophysical 3-D digital model of the crustal sector involved in the sequence, (2) reproduce the earthquake ground motion at some seismological stations through physics-based numerical simulations and (3) compare the observed recordings with the simulated ones. In this way, we investigate how the earthquake ground motion in the epicentral area is influenced by local stratigraphy and geological structure buried under the Po Plain alluvium. Our study area covers approximately 5000 km2 and extends from the right Po River bank to the Northern Apennine morphological margin in the N–S direction, and between the two chief towns of Reggio Emilia and Ferrara in the W–E direction, involving a crustal volume of 20 km thickness. We set up the 3-D model by using already-published geological and geophysical data, with details corresponding to a map at scale of 1:250 000. The model depicts the stratigraphic and tectonic relationships of the main geological formations, the known faults and the spatial pattern of the seismic properties. Being a digital vector structure, the 3-D model can be easily modified or refined locally for future improvements or applications. We exploit high-performance computing to perform numerical simulations of the seismic wave propagation in the frequency range up to 2 Hz. In order to get rid of the finite source effects and validate the model response, we choose to reproduce the ground motion related to two moderate-size aftershocks of the 2012 Emilia sequence that were recorded by a large number of stations. The obtained solutions compare very well to the recordings available at about 30 stations in terms of peak ground velocity and signal duration. Snapshots of the simulated wavefield allow us to attribute the exceptional length of the observed ground motion to surface wave overtones that are excited in the alluvial basin by the buried ridge of the Mirandola anticline. Physics-based simulations using realistic 3-D geomodels show eventually to be effective for assessing the local seismic response and the seismic hazard in geologically complex areas.
- Article
(8694 KB) - Full-text XML
-
Supplement
(4691 KB) - BibTeX
- EndNote
Computer-aided three-dimensional (3-D) geological modeling (e.g., Mallet, 2002) is becoming an increasingly important tool in geoscience studies for both the management of natural resources and the prevention of natural disasters. 3-D geological modeling allows the combination of multi-disciplinary data in the shaping and visualization of the current knowledge of the geological structures and allows integration with new data or interpretations, as they become available (Calcagno, 2015). Moreover, 3-D geological models represent the basis for the execution of physics-based numerical simulations, provided that a reliable scientific procedure is defined to convert the different types and levels of the available complex geological information into that needed by the proposed numerical simulation at the predefined scale level (e.g., Fischer et al., 2015).
The present study concerns the setup of a 3-D structural model starting from geological data and the development of the corresponding geophysical model by assigning viscoelastic properties to each structural unit. The scope of the final 3-D geophysical model is to allow physics-based forward modeling of seismic wave propagation aimed at (1) explaining the ground motion peculiarities observed in past earthquakes and (2) increasing the reliability of ground motion predictions for possible future events (e.g., Moczo et al., 2014; Taborda and Roten, 2015; Cruz-Atienza et al., 2016). Our study focuses on the Emilia region (northern Italy), where in 2012 a relevant seismic sequence featuring the two mainshocks, MW 6.1 on 20 May 2012 at 02:03:53 UTC and MW 5.9 on 29 May 2012 at 07:00:03 UTC (Rovida et al., 2016), occurred (Fig. 1).
Seismic-hazard studies are usually based on the empirical–statistical method, which makes use of ground motion prediction equations (GMPEs) (e.g., Barani et al., 2017a, b), with possible corrections deduced from local geological conditions (Grelle et al., 2016). However, occasionally the observed ground motion characteristics deviate considerably from the empirical–statistical predictions. Those deviations imply the presence of case-specific features in wave generation or propagation (e.g., complex fault ruptures, complex geological structures, such as deep basins), which are not adequately considered in the derivation of the GMPE. In order to predict the effects of these features, we may apply numerical–deterministic methods.
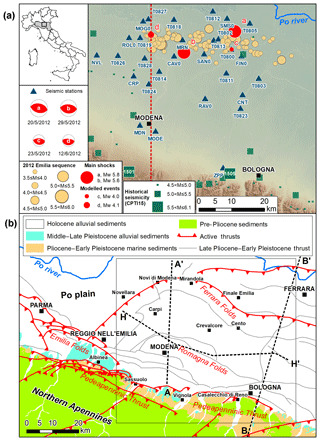
Figure 1(a) Study area with historical seismicity (CPT15; Rovida et al., 2016), 2012 Emilia sequence epicenters (M≥3.5), temporary/permanent seismological stations and trace of vertical section of Fig. 11. (b) Geological sketch of the study area, with traces of the three deep geological sections represented in Fig. 2.
An emblematic case of such deviations occurred during the 2012 Emilia seismic crisis, when unexpectedly long duration and large peak ground velocity (PGV) characterized the earthquake ground motion at some sites in the epicentral area (Priolo et al., 2012; Castro et al., 2013; Luzi et al., 2013; Barnaba et al., 2014; De Nardis et al., 2014). Those deviations have been attributed to the complexity of the geological structure beneath the Po Plain, which features a very large and deep alluvial basin bounded by two largely buried thrust-and-fold systems, the Northern Apennine chain in the south and the southern Alpine ridge in the north, respectively (Boccaletti et al., 1985). In order to explain quantitatively the observed ground motion characteristics, we have built a 3-D model that describes the morphology of the buried geological structure and assigns viscoelastic properties (mass density, elastic modula and elastic quality factors) to each formation, so that it can be used for physics-based numerical modeling of the seismic wave propagation in the studied volume.
Our model is not the first 3-D model that was developed for the Po Plain area. At least three research groups have carried out 3-D numerical computations of the earthquake ground motion in the Po Plain so far. A first study was performed by Vuan et al. (2011), who simulated long-period (T>5 s) surface waves generated in the basin by strong (MW>6) earthquakes. They used a 3-D model featuring realistic, irregular basin edges and a simplified depth-dependent velocity profile for the sedimentary filling of the basin. A more complex 3-D geological model was set up by Molinari et al. (2015) for simulating the earthquake ground motion in the long-period band (T>3 s). The simulated waveforms were compared only qualitatively with the recorded waveforms at some far-source stations in order to demonstrate the effectiveness of the 3-D geological model. A third model is the one developed by Paolucci et al. (2015), who simulated the near-source strong ground motion for the MW 6.1 20 May 2012 earthquake in the frequency range 0.1–1.5 Hz. The overall satisfactory agreement of their simulated waveforms with the empirical records is due to two key elements: the extended source model (i.e., slip distribution and rupture propagation) and the 3-D structural model, which contains only two main geologic interfaces (i.e., the base of the Pliocene formation and that of the Quaternary deposits). In particular, the satisfactory simulation of the surface waves' trains stems mainly from the shape of the interface of the base of the Quaternary deposits. We have to mention also Turrini et al. (2014), who defined the whole structure of the Po basin from its deep roots, at the Moho level, through an exhaustive analysis of all the existing structural–geological and geophysical studies. They summarize the current knowledge of the Po Basin structural geology into a digital, editable model that can be used to improve the geodynamic interpretation of the area. However, their model does not contain any geophysical parameterization, nor does it reach the level of detail that is required in our study.
Among the cited works, only Paolucci et al. (2015) provided the elements for understanding the peculiar features of the near-source strong motion observed during the 2012 events (such as the propagation of prominent trains of surface waves in the northern direction), by adopting a reasonably simple 3-D model of an area centered on the 2012 MW 6.1 mainshock epicenter. In the present work, we instead focus on the southern sector of the 2012 epicentral area, characterized by a very deep basin with sediment thickness exceeding 8000 m in some points. In order to investigate the effects of this complex geological setting, we set up a 3-D geological model with unprecedented detail of a limited area of the Po Plain, bounded by the right Po River bank in the north and the Northern Apennine morphological margin in the south, and located between the two chief towns of Reggio Emilia in the west and Ferrara in the east (Fig. 1). The area includes the epicenters of the 2012 seismic sequence as well as some other potential seismogenic structures (DISS Working Group, 2018). In order to set up the 3-D geological model, we considered only data available in scientific literature. The physical properties assigned to the geological units were deduced from literature as well. We relied on the commercial GeoModeller software released by Intrepid Geophysics for merging and interpolating the geological data in a 3-D digital model, which constitutes the input for numerical simulations of the earthquake ground motion and represents a basis for further improvements when new data will be available. In this first version, denoted ER3D, the model is based on the elaboration of a digital terrain model, a seismotectonic map and three deep geological sections crossing the study area, as well as the isobaths of two interfaces between some relevant geological formations. As discussed in Sect. 3.2, the detail level included in this model is consistent with numerical computations of the ground motion in the frequency range up to 2 Hz and therefore comparable to the frequency range of the computations performed by Paolucci et al. (2015).
We performed the computations of the ground motion by applying the high-performance computing (HPC) FPSM3D code (Klin et al., 2010), dedicated to the numerical modeling of the propagation of viscoelastic waves in heterogeneous media. The FPSM3D code is based on the Fourier pseudo-spectral method for the solution of hyperbolic equations; its accuracy performance compares well with other computer codes used in the scientific community for the 3-D simulation of the earthquake ground motion in alluvial basins, as has emerged during recent verification exercises (Maufroy et al., 2015; Chaljub et al., 2015). The validation of the constructed 3-D geological model consisted in a comparison in terms of PGV and duration, between the numerical predictions and the empirical recordings of two 2012 events at the several stations that were deployed in the area during the seismic sequence (Fig. 1). In order to put in evidence on the peculiarities of the ground motion that are due only to propagation effects, we considered two weak events (MW 4.0 and 4.1) that can be modeled using a point source, and not the mainshocks, which would require a finite source model. The computations were run using the HPC resources of the CINECA consortium in Bologna.
The fundamental step for physics-based numerical prediction of the earthquake ground motion consists in the setup of a 3-D model of the geological structure. In order to set up a reliable geological model, we need a sound geological interpretation of well-constrained geophysical data. Thanks to oil exploration and research widely undertaken since 1960, a comprehensive synthesis of the structural features of the Po Plain subsurface was possible in the past decades (e.g., Pieri and Groppi, 1981; Fantoni and Franciosi, 2010; Boccaletti et al., 2011; Martelli et al., 2017). In the following, we give an overview of the known geological features of the study area and describe how we synthetized these data in a digital 3-D structural model. Finally, we discuss how we assigned the physical properties to each geological formation for characterizing the 3-D model also from a geophysical point of view.
2.1 Geological and seismotectonic setting of the study area
The study area is in the Emilia-Romagna region (northern Italy), and specifically it occupies the sector of the Po Plain between Reggio Emilia (west) and Ferrara (east), as shown in Fig. 1. The Po Plain is a foredeep–foreland zone interposed between two chains with opposite vergence: Northern Apennines to the south and Southern Alps to the north. Terrigenous sediments originating from the erosion of the two growing chains accumulated in the basin (Dondi et al., 1982): first those of alpine origin (Miocene–Quaternary), then those of Apennine provenance (Pliocene–Quaternary). From the Middle Pleistocene, the sedimentation is mainly continental and results from the depositional activity of the Po River and its tributaries. The substrate of the terrigenous sediments is made up by a carbonatic succession of mainly Mesozoic age, whose top consists of marly sediments of Paleogene age. This carbonate succession is separated from the metamorphic basement by a thick evaporite succession of Triassic age (Fig. 2). From the tectonic point of view, the area is affected by numerous compressive structures, with northern vergence (Fig. 1). The southern zone, coinciding with the Apennine hills between the Albinea, Sassuolo, Vignola and Casalecchio di Reno municipalities, is characterized by the reverse faults of the Pedeapenninic thrust (Boccaletti et al., 1985), which is responsible for the morphological transition between the Northern Apennines and the Po Plain. Subsoil investigations for oil exploration (Pieri and Groppi, 1981) showed that the Apennine outer front does not coincide with the Apennine–Po Plain morphological margin and that in the Po Plain subsoil many blind faults and folds are present. Actually, the Apennine outer front is located in the subsoil around the present course of the Po River, coinciding with the reverse faults of the Ferrara folds overthrusting the Lombardy–Veneto monocline (Fig. 1). The main detachment and overlap levels of thrusts are the Triassic evaporites, embedded between the underlying metamorphic basement and the overlying succession made of Late Triassic–Oligocene carbonates, Oligo-Miocene marls and more recent terrigenous sediments (geological sections in Fig. 2). The southernmost buried structures, characterizing the subsoil of the plain between Reggio Emilia, Modena and Bologna, are the eastern termination of the Emilia folds and the western termination of Romagna folds. The northernmost structures are in the subsoil between Novellara, Mirandola and Finale Emilia, where they constitute the western arc of the Ferrara folds (Fig. 1), giving rise to a very pronounced ridge, whose top is very close to the surface between Novi di Modena and Mirandola (Laurenzano et al., 2017). A large part of the interest area, in particular the central zone between Modena, Carpi and Cento, comprised between the Pedeapenninic thrust and the Ferrara folds, corresponds to a very deep syncline: the thickness of the Plio-Quaternary sediments between Modena and Crevalcore exceeds 8500 m (Pieri and Groppi, 1981).
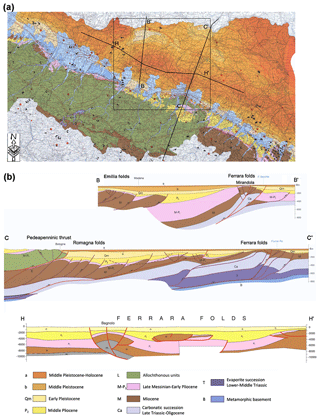
Figure 2(a) Portion of the seismotectonic map. Black lines represent the three geological section traces. (b) Geological cross-sections from the Apennine–Po Plain margin to the Po River (from Boccaletti et al., 2004).
The relationships between tectonic structures, sedimentary bodies and the surface morphology indicate that Pedeapenninic thrust and Ferrara folds were active also in recent times, as demonstrated by the Quaternary deposits which are deformed and uplifted. Conversely, the Emilia and Romagna folds were active mainly in the Pliocene, being the Quaternary deposits not deformed by these structures but included in the syncline between the Pedeapenninic thrust and the Ferrara folds (Pieri and Groppi, 1981; Burrato et al., 2003; Boccaletti et al., 2004, 2011; Martelli et al., 2017).
The entire area is seismically active, and the distribution of historical and instrumental earthquakes seems to confirm the major actual activity of the Pedeapenninic thrust and the Ferrara folds. In fact, the main historical earthquakes of the area have been located along the Apennine–Po Plain margin (Rovida et al., 2016), while the Ferrara folds are responsible for the earthquakes on 20 and 29 May 2012, respectively, MW 6.1 and MW 5.9 (Fig. 1). For these reasons, these structures are included in the database of the seismogenic structures capable of generating strong earthquakes (DISS Working Group, 2018). The instrumental data indicate that in this area the biggest part of earthquakes has a compressional source mechanism (Pondrelli et al., 2006), and that the hypocentral depth (http://cnt.rm.ingv.it, last access: 27 May 2019) in the northern zone (Ferrara folds) is concentrated in the first 15 km, while in the Apennine–Po Plain margin greater depths (15–35 km) are common.
2.2 Integration of geological data in the 3-D digital model
Geological 3-D modeling consists in the representation of a solid Earth sector by using surface and subsurface data in a computer-aided process (Mallet, 2002), which allows to shape and to visualize the current knowledge and/or to update it with new data. Numerous methodologies were implemented in several packages dedicated to the geological 3-D modeling. The package we adopt for the present work is GeoModeller (Guillen et al., 2004; Calcagno et al., 2006, 2008), a commercial software originally developed by the French Bureau de Recherches Géologiques et Minières (BRGM) and more recently by the Intrepid Geophysics (http://www.geomodeller.com, last access: 27 May 2019). GeoModeller is a software tool for the integration of different geometrical, geological and geophysical data in a geometrically coherent 3-D geological model. The procedure is based on the potential-field interpolation (Lajaunie et al., 1997) and is particularly well suited for when the available geological data consist only in some geological maps, sparse cross-sections or boreholes. The method requires as input the location of the geology interfaces and orientation data at some points. The theory behind the method describes the 3-D geologic surfaces as isopotential surfaces of a scalar potential field, with orientation vectors playing the role of the field's gradient. The stratigraphic pile is defined by the chronological order of the strata and the relationships between the formations in terms of either “onlap” or “erode”. The complex geology is described by different domains, each characterized by a geological series, separated by stratigraphic or tectonic discontinuities. For each domain, the geology is modeled by a set of subparallel, smoothly curving surfaces using the potential-field functions. Co-kriging is used to obtain a solution that honors the input data (McInerney et al., 2005). Faults are taken into account as discontinuous drift functions into the co-kriging equations (Chilès et al., 2004). Refer to Calcagno et al. (2008) for a more comprehensive description of the methods implemented in GeoModeller.
To build the 3-D geological model of central Emilia, we considered a crustal volume with 70 km ×70 km area and depth of 20 km, in order to include most of the 2012 seismic sequence hypocenters, associated with the deepest segments of the active thrusts. We defined the stratigraphic pile according to the one reported on the seismotectonic map of the Emilia-Romagna region (Boccaletti et al., 2004; Martelli et al., 2017). We imported the following data into GeoModeller:
-
a high-resolution digital terrain model at a grid size of 10 m, provided by the Regione Emilia-Romagna Technical Office (DTM lidar; Ministero dell’Ambiente e della Tutela del Territorio e del Mare) as raster image;
-
an excerpt of the seismotectonic map of the Emilia-Romagna region at a scale of 1:250 000 (Boccaletti et al., 2004), which reports the main geological units outcropping in the area, as well as the active (and potentially active) tectonic structures;
-
two deep geological sections with a scale of 1:250 000 (Boccaletti et al., 2004), constrained by borehole data and derived by interpreting reflection seismic profiles acquired in the area, which cross the study area in the NNE–SSW direction, transversally to the Apennine chain axis (traces A–A' and B–B' in Figs. 1 and 2);
-
a deep geological section with a scale of 1:250 000 (Boccaletti et al., 2004), which crosses the study area in the WNW–ESE and W–E directions, longitudinally to the Apennine chain axis (trace H–H' in Figs. 1 and 2);
-
isobaths of the plain deposits' bottom (Formation A with age 0.45 Myr in Fig. 3a) (Martelli et al., 2017).
-
isobaths of the Pliocene sediments' bottom (Formation MP with age 6.3 Myr in Fig. 3b) (CNR, 1992)
The geological cross-sections of Boccaletti et al. (2004) and Boccaletti et al. (2011) are based on more recent seismic profiles than those used by Pieri and Groppi (1981) and take into account also stratigraphic data derived from Di Dio (1998), for the definition of the superficial part (down to a depth of approximately 300–400 m).
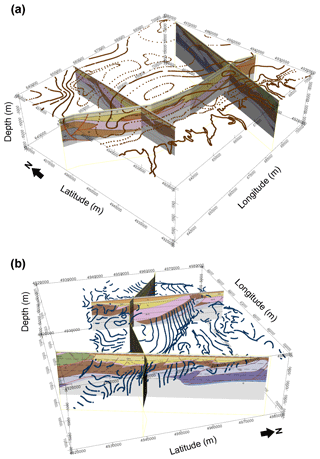
Figure 3Geological cross-sections and 3-D surfaces. (a) Southwest view and base of the plain deposits (Formation A); (b) east view and base of the Late Pliocene (Formation MP).
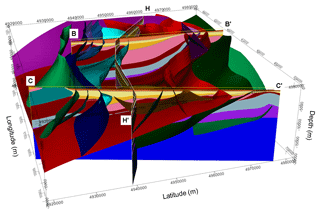
To constrain the geometry of the geological bodies, we manually digitized the interfaces separating the oldest geological formations, both on the excerpt of the seismotectonic map and on three mentioned geological cross-sections, and merged them with the digital data outlining the isobaths of the two youngest formations' bottoms. Similarly, we digitized the fault traces on the cross-sections and attributed them their extension, their relationship with the geology series (in order to take into consideration the faults when interpolating the geology series) and their relationship with other faults (to define the termination of one fault on another). The building process consisted in several steps, with a progressive integration of the available data, starting from the top surface. At each step, we performed a computation of the implicit surfaces of the formation boundaries and reviewed the partial result before adding new elements. If new data are available for the project, we can obtain a revised model with little effort. The 3-D model obtained for the Emilia region is displayed in Figs. 4, 5 and 6. Two different views of the model sampled on the three input geological cross-sections are shown in Fig. 4. Figure 5 shows four parallel equally spaced north–south 2-D vertical sections across the investigated volume, while Fig. 6 evidences the surfaces corresponding to the fault system. A complete view of the 3-D model is available in the pdf file with 3-D content that is provided as the Supplement to this article. In order to use the model for numerical simulations, we exported it into voxet format by sampling the geological formation volumes with a regular 3-D grid.
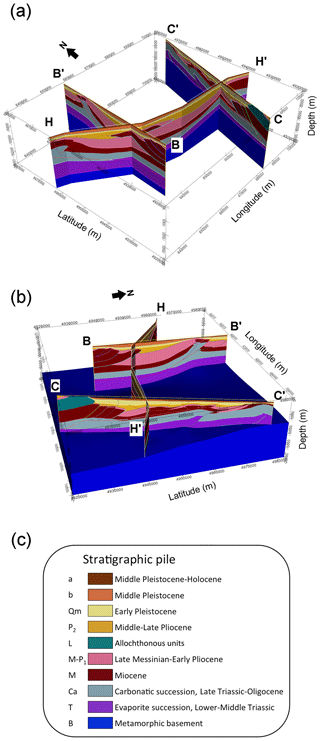
Figure 4Model plotted on the three sections: (a) a southwest view, (b) an east view and (c) the stratigraphic pile corresponding to the seismotectonic map of Boccaletti et al. (2004).
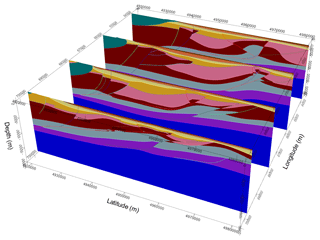
Figure 53-D model: four equally spaced north–south 2-D vertical sections across the investigated volume. Stratigraphic pile as in Fig. 4c.
2.3 Physical properties of geological formations
In order to perform the physics-based numerical simulations of the seismic wave propagation, we have to assign the values of the physical properties to each 3-D geological volume. Considering valid the assumption of an isotropic and viscoelastic medium, we assigned to each formation the values of the following parameters:
-
the velocities VP and VS of the compressional and the shear seismic wave, respectively;
-
the mass density ρ;
-
the elastic quality factors QK and Qμ for bulk and shear deformations, respectively.
We assumed that each geological formation belonging to the stratigraphic pile of Fig. 4 is characterized by different values of the abovementioned parameters. In order to simplify the assignment of the physical properties values to each formation, we decided to characterize each unit only by VP and to evaluate from the latter the other four properties using some well-established empirical relations.
Considering the velocities expressed in km s−1, we adopted the following relation:
which was found by Brocher (2005) from a large number of measurements made in a variety of lithologies including Quaternary alluvium and Miocene sedimentary rocks, which constitute a fundamental part of our model. We also adopted the well-established relation,
found by Gardner et al. (1974) for the mass density ρ in g cm−3 and VP in km s−1. The intrinsic attenuation is described with the shear quality factor, which is evaluated from VS expressed in km s−1 with the widely used rule of thumb (e.g., Paolucci et al., 2015):
and with the bulk quality factor, whose value is set as
in accordance with the theory exposed by Morozov (2015). We assumed that the value of VP assigned to each geological formation might depend on the depth through a linear gradient:
The values of the coefficients VP(0) and ∂zVP for each formation are given in Table 1. From Table 1, it appears that in most formations a constant value for VP is assumed. The VP value in Formation A has been set to 1.5 km s−1, which corresponds to the velocity of the compressional seismic waves in water saturated soils. The values in the deeper formations were chosen in accordance with VP values of the geological formations in the Po Valley basin published by Montone and Mariucci (2015).
Table 1Physical quantities assigned to each geological formation. VS, ρ, Qμ and QK are evaluated from VP according to Eqs. (1)–(4).
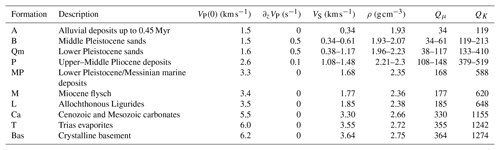
We tested the validity of Eq. (1) by analyzing the consistency of the predicted VS with some measures of VS resulting from geophysical surveys performed in the Po Plain. According to Eq. (1), the value VP=1.5 km s−1 assigned to the uppermost formation (Formation A) (Table 1) – having a thickness of the order of 100 m on most of the area – turns out as VS=0.34 km s−1. This value is compatible with the average value found for VS with the extended spatial autocorrelation (ESAC) method by Priolo et al. (2012) at three different sites of the Po Plain in a similar formation down to a depth of 120 m. At larger depth, the proposed geological model presents significant lateral heterogeneities and could not be directly compared with the existing 1-D VS profiles that were derived from surface waves' dispersion by Malagnini et al. (2012) and Milana et al. (2014) in the frequency bands of 0.083–0.33 and 0.15-–0.70 Hz, respectively. For example, in the depth range between 2 and 4 km, our model features the simultaneous presence of very different formations, such as the Miocene and Late Messinian–Early Pliocene formations (M and MP, respectively, with VS on the order of 1.7 km s−1) and the Carbonatic succession (Ca, with VS velocity as high as 3.3 km s−1). On the other hand, the two 1-D velocity structures previously cited feature velocities between VS=2.0 and VS=2.5 km s−1 within the same depth range, which are compatible with the average value of the VS values found in our model.
The computation of seismic wave propagation in alluvial basins at frequencies of engineering interest represents a demanding task. The geometrical complexity requires the adoption of numerical computational methods for the solution of the viscoelastodynamic equation, which governs the ground motion during an earthquake. The wide range of wave velocities involved in realistic simulations imposes a fine sampling of the spatial and temporal domains. The computational cost of typical applications dictates the usage of parallel algorithms suitable for exploiting HPC resources.
3.1 The FPSM3D code
In order to compute the seismic waves propagation in the constructed 3-D geological model, we adopted the FPSM3D code (Klin et al., 2010), which is based on the Fourier pseudo-spectral method (FPSM) for the integration of hyperbolic equations. The peculiarity of FPSM – first introduced by Kreiss and Oliger (1972) – consists in the evaluation of the spatial derivatives by means of a multiplication in the wavenumber domain. The transition from the spatial domain to the wavenumber domain, and back, is performed by means of the fast Fourier transform. FPSM combines the optimal accuracy of the global spectral differential operators and the simplicity of the spatial discretization with a structured rectangular grid. According to the Nyquist’s sampling theorem, FPSM works with a relatively coarse spatial sampling (Fornberg, 1987), which represents a valuable advantage when solving 3-D problems. The FPSM3D code performs the time integration by means of the second-order explicit finite-difference (FD) scheme and adopts the convolutional perfectly matching layer (C-PML) approach (Komatitsch and Martin, 2007) to prevent the effects of the spatial domain boundaries on the computed wavefield. The effects of the staircase approximation of the material interfaces in the regular grid are avoided using the volume harmonic averaging of the elastic moduli and volume arithmetic averaging of the mass density, as proposed by Moczo et al. (2002). The adequateness of the FPSM3D code in this kind of applications is demonstrated in the works by Chaljub et al. (2015) and Maufroy et al. (2015), aimed to estimate the accuracy of a number of numerical methods currently used for physics-based predictions of earthquake ground motion in 3-D models of sedimentary basins.
3.2 Setup for the computations
A critical step in the setup for the numerical simulations consists in the choice of the frequency range. In order to reproduce accurately the wave propagation at high frequencies, it requires a fine spatial and temporal sampling and therefore a larger computational effort. On the other hand, the simulation of wavelengths much shorter than the dimensions of the heterogeneities in the model would be out of scope. We have chosen the maximum frequency (fmax) according to the detail of the 3-D geological model. The most superficial structural unit (i.e., Formation A) presents a variable thickness H>50 m on a large part of the studied area and in particular at all the station locations. Considering that the average shear wave velocity assigned to this unit is about VS=0.33 km s−1, the fundamental resonance frequency (f0) of the upper layer results below 1.65 Hz, if we apply the known relation . In order to model the effects of the upper layer on the wavefield, we have to set fmax>f0. On the other hand, the lack of detail in the shallower part makes the model unsuitable for realistic computations at frequencies much higher than f0; thus, we set fmax=2 Hz.
The numerical computations were performed using the spatial and temporal sampling as exposed in Table 2. The spatial domain consisted in a box with a 61.4 km wide square basis and 22 km height. The vertical sampling of the spatial grid was shrunk towards the top surface in order to sample accurately the smaller wavelengths that characterize the seismic wavefield there. The flat topography of the studied area allowed us to neglect possible topographic effects. The Courant stability criterion dictated a time sampling step as short as 0.005 s, and 65 s long time series of the ground motion were extracted in all the grid points at surface and on the two east–west and north–south vertical sections crossing the epicenter of the simulated events. We selected the length of the simulated seismograms in order to include the part of the signal that is significant for our purposes at the farthest station considered in the comparisons. The computational cost of each simulation was about 50 000 core hours on the IBM-BG/Q supercomputer at CINECA.
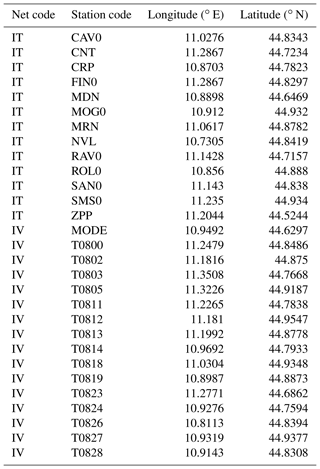
In order to investigate whether the ER3D model is able to reproduce the peculiar features of the observed earthquake ground motion, we performed a comparison between the ground motion recorded by 29 seismological stations deployed in the study area during the 2012 seismic sequence – see Fig. 1 and Table 4 – and the numerically predicted ground motion at the same locations. The considered seismic stations belong to the Italian Strong Motion Network (IT) managed by the Civil Protection Department (DPC) and to the Italian National Seismic Network (IV) managed by the National Institute of Geophysics and Volcanology (INGV). For reference, we considered also the physics-based numerical predictions resulting from the simplified model PADANIA (Malagnini et al., 2012), which is composed of horizontal homogeneous layers (therefore, a 1-D model in contrast to our 3-D). The numerical simulations regarding the PADANIA model were performed using the wavenumber integration method (WIM) (Herrmann, 2013), which solves the wave equation in a horizontally layered medium. The synthetic seismograms contain all the phases and are accurate in both the near and far fields.
4.1 The simulated earthquake ground motion
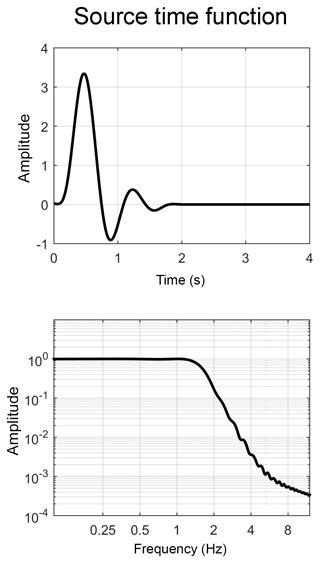
In order to focus the study on the propagation of seismic waves rather than on their generation, we decided not to consider the mainshocks of the 2012 Emilia sequence, which were simulated in previous works concerning the 3-D modeling of the Po Plain (e.g., Molinari et al., 2015; Paolucci et al., 2015). For those events, of magnitude MW 6.1 (on 20 June 2012) and MW 5.9 (on 29 May 2012), respectively, the effects of the peculiarities of the seismic source in the recorded waveforms are not negligible. Since the main topic of this work is the estimation of the wave propagation effects on the earthquake ground motion (in particular, the influence the Po Plain underground geological structure has on the wave propagation), we decided to simulate events of lower magnitude. With an upper frequency limit of 2 Hz (see Sect. 3.2), we can roughly assume that the complexities (i.e., unpredictable irregularities in the spatial extension and time evolution) in the seismic sources are negligible for earthquakes up to MW 4.0. Nevertheless, such events are strong enough to be well recorded in almost all the considered stations. We therefore computed the seismic wavefield for the two MW≃4.0 events listed in Table 3 with sources located at the NE and NW ends of the studied area (events labeled c and d in Fig. 1). The hypocenters and the magnitude of these events were taken from the latest relocation study (Lavecchia et al., 2015). The generation of the wavefield was modeled as a double-couple point source with a time function corresponding to the low-pass minimum-phase Butterworth filter plotted in Fig. 7 and with an inverse focal mechanism, in accordance to the fault plane solutions of the 2012 sequence found by Saraò and Peruzza (2012).
4.2 Comparison with the empirical earthquake ground motion
The permanent and temporary seismological stations deployed in the study area during 2012 are mapped in Fig. 1 and listed in Table 4. The time series recorded at these stations during the two events listed in Table 3 are available from the Italian strong motion database ITACA (ITACA, 2019; Pacor et al., 2011). Event epicenters and station locations are shown in Fig. 1. Since the empirical time series have a much wider frequency content than the simulated ones, they were low-pass filtered using the same minimum-phase Butterworth filter plotted in Fig. 7, which was used as the source time function in the numerical simulations.
We compared the simulated ground motion with the empirical one in terms of horizontal peak ground velocity (PGV) defined as the peak modulus of the vector sum of the two horizontal components and in the duration defined as the time interval length between 5 % and 95 % of the Arias intensity (Arias, 1970). The vertical component was excluded from this comparison since it was systematically lower than the horizontal ones.
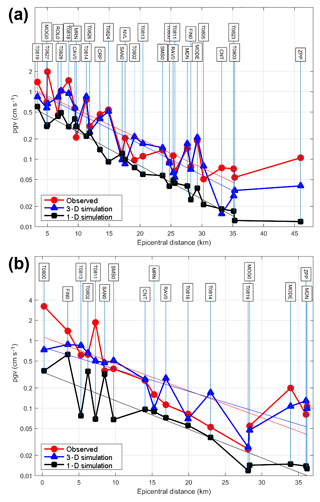
Figure 8Observed and numerically simulated PGV (peak value of the two horizontal components) at the considered stations, plotted in function of the epicentral distance. (a) The 12 June 2012 MW 4.1 event. (b) The 23 May MW 4.0 event. The ordinate scale is logarithmic.
In Fig. 8, we plot – separately for the two events – the logarithm of the measured and computed PGVs at each station against the epicentral distance. We represent there also the linear fit for the three series of data: empirical, 3-D model (ER3D) and 1-D model (PADANIA). The plot shows that, in both cases, the 3-D model numerical predictions fit the observations better, whereas the 1-D model prediction underestimates the observed PGV at most stations (by a factor of almost 2). The high variability shown by stations at similar epicentral distance is probably due to the different source–station azimuth and focal mechanism–radiation pattern. As observed in Maufroy et al. (2015), the uncertainty in source characteristics may impact the numerical predictions especially at short distances. The remarkable underestimation of PGV for event 2 at station T800, located just above the hypocenter, is therefore not too surprising and could be attributed to the combined effect of inaccurate hypocentral location, focal mechanism and near-source heterogeneities. In fact, considering that source 2 has a dip of 33∘ (Table 2), T800 is near to the P-wave radiation maximum and at the margin of the S-wave lobe. Figure 10d confirms this interpretation: the simulated seismogram features a pronounced P-wave amplitude in the vertical component, if compared to the S-wave one. On the other hand, in the same figure (Fig. 10d), the recorded seismogram presents a reversed picture: the relatively weak P wave (smaller than the simulated one) and strong S wave indicate that the actual source characteristics are different from what we assumed.
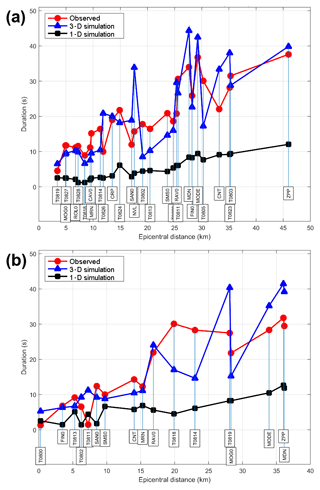
Figure 9Observed and numerically simulated duration (defined as intervals between 5 % and 95 % of the Arias intensity) at the considered stations, plotted in function of the epicentral distance. (a) The 12 June 2012 MW 4.1 event. (b) The 23 May MW 4.0 event.
Similarly, in Fig. 9, we plot the duration of the measured and computed ground motions against the epicentral distance. Again, the 3-D model numerical predictions fit better the observations than the 1-D model predictions, which underestimate the duration at almost all the stations. In particular, it can be observed how the 3-D model is able to predict quite well the very long duration values observed at some stations located in the southern part of the model (for example, the MDN, MODE and ZPP stations for the event labeled “d” in Fig. 1). In order to analyze the reasons of the exceptional length of the observed ground motion, we analyze, in the following section, the snapshots of the wavefield propagation across a north–south vertical section that encompass both the source of event d and the neighborhoods of the station MODE.
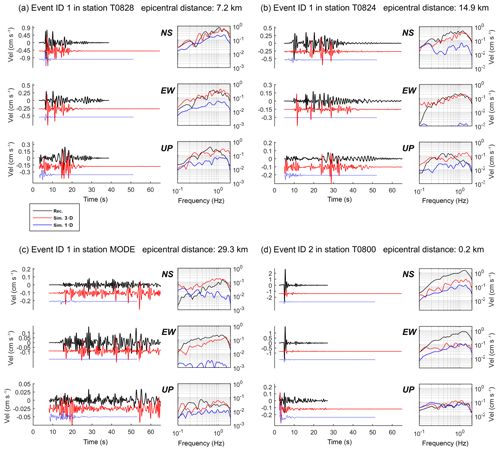
Figure 10Comparison between recorded (in black) and predicted (in red is the 3-D model and in blue the 1-D model) ground velocity time series and Fourier amplitude spectra in four cases. (a–c) The June 2012 MW 4.1 event at three stations (T0828, T0824 and MODE), southward of the epicenter: the ground motion predicted from the 3-D model results significantly more consistent with the observations than the one predicted from the 1-D model. (d) The May 2012 MW 4.0 event in station T0800 just above the hypocenter: the underestimation of the S-wave peak and the overestimation of the P-wave peak suggest that the actual source mechanism could be different from what we assumed (see text).
4.3 Wave propagation across a vertical profile
A remarkable advantage of 3-D numerical modeling consists in the possibility to visualize the wave phenomena, which cause unexpected features in the observed ground motion. The most apparent anomalies in the observed ground motion that were reasonably well predicted with the 3-D model are the PGV and the long duration at the stations south of the epicenter during the 12 June 2012 MW 4.1 event (event ID 1 in Table 3 and labeled “d” in Fig. 1). In Fig. 10a, b and c, we compare the empirical and the computed time series at stations T828, T824 and MODE. Even though we could not reach a match between the time series in a strict sense, the results obtained with the 3-D model represent a significant improvement if compared to the 1-D model results.
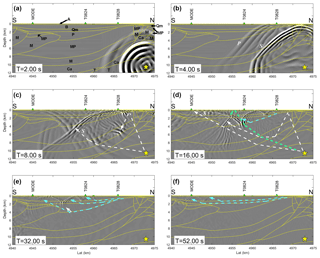
Figure 11Numerically evaluated seismic wavefield for the June 2012 MW 4.1 event across the south–north vertical section represented in Fig. 1 (red dashed line). Green triangles: projection of the nearby station locations. Yellow star: hypocenter. Yellow lines: interfaces among structural units. (a) Snapshot taken after 2 s of propagation. Black letters: structural unit identifiers – see Table 1. (b) Snapshot taken after 4 s of propagation. P and S: wavefronts of the compressional and shear body waves, respectively. (c) Snapshot taken after 8 s of propagation. (d) Snapshot taken after 16 s of propagation. The S waves dominate the scene. The dashed turquoise line denotes the ray path of the waveform reflected from the surface; the dashed cyan line denotes the total reflection on the interface between the MP and P units. (e, f) Snapshots taken after 32 and 52 s of propagation, respectively. Surface wave overtones are clearly visible in the soft soil layers in the upper part of the structure. The dashed cyan lines evidence the wave trains as well as the corresponding interfaces that originate the total reflection. The full sequence of snapshots is available as a movie file on the Open Science Framework (Klin, 2019).
In order to investigate the cause of the particular features of the ground motion in these stations, we can follow the modeled propagation of the seismic waves on a vertical profile extracted from the 3-D spatial domain (Fig. 11), whose trace on the surface is shown by the red dashed line in Fig. 1. The profile cuts the volume in the south–north direction and includes the source of the 12 June 2012 MW 4.1 event (labeled “d” in Fig. 1) in the northern part of the section as well as the neighborhood of the T828, T824 and MODE stations (represented with green triangles) in the central and southern parts. The grey shadow on the profiles represents the wave amplitude, whereas the yellow lines represent the interfaces between the structural units. For the sake of clarity, the structural units are labeled in Fig. 11a only. The profile samples three different areas of the geological structure: the northern, central and southern parts. The northern area is characterized by the Ferrara folds (Fig. 1), where high-velocity layers (VS=1.7 km s−1) are lifted up to few tens of meters below the surface. The central area is characterized by a deep syncline with thick, low-velocity (VS<1 km s−1) superficial layers of sediments and alluvial deposits. In the southern part, we find the Emilia folds, which again reduce the thickness of the soil cover. In the first snapshot, taken after 2 s of propagation (Fig. 11a), we can see the initially concentric wavefronts propagating from the source located in the Ferrara folds. After 4 s (Fig. 11b), the wavefronts propagating towards south assume an almost plane shape, after having been deformed in the slower formations of the basin. We can clearly discern the compressional waves (denoted by the letter P), and the shear waves (denoted by the letter S), the latter stronger and slower, with a shorter wavelength. After 8 s (Fig. 11c), the direct S has reached T828 and we can observe how at that time the S wave is reflected from the soil surface above the ridge and channeled in the dipping layers south of it. Because of the layers' dip, the reflected S wave hits the layers at a post-critical angle and generates a number of diffracted waves, which correspond to surface wave overtones, if we adopt a mathematically more elegant formalism. After 16 s (Fig. 11d), the aforementioned diffracted waves can be well recognized in the profile across the wavefield and we can associate them with the strong phases following the direct S arrival at the three considered stations.
For example, the strong wave train predicted at T824 between 16 and 20 s of propagation (Fig. 10b) corresponds to the refracted wave on the interface between layers P and MP. The subsequent wave trains at about 23 and 28 s correspond to the refraction on the Qm-P and B-Qm interfaces, respectively, as it appears from the snapshot at 32 s (Fig. 10e). The refraction on these three interfaces originates also the three most evident wave trains at the end of the signal at MODE, as can be understood from Fig. 10e and f.
The lack of a stricter match between the predicted and observed wave trains can be ascribed to the uncertainties in the layer geometries and physical properties and does not affect the explanation we provided here for the long duration of the ground motion in the stations south of the 12 June 2012 MW 4.1 epicenter.
The study attests the importance of considering possible 3-D heterogeneities in the geological structure in the estimation of the expected earthquake ground motion. The test case consists in the well-documented 2012 seismic crisis in Emilia-Romagna (Italy), in the middle of the Po Plain. The alluvial valley of the Po Plain presents a complex geological architecture, which may locally cause an aggravation of the ground motion during an earthquake. In order to explain the ground motion observed during some earthquakes of the 2012 Emilia seismic crisis, characterized by unexpectedly long duration and large PGV, we developed a 3-D digital geological model of a limited area (a square with 70 km long side) of the Po Valley basin by considering already published geological and geophysical data. We applied physics-based 3-D numerical modeling to predict a posteriori the anomalous ground velocity duration and peak values from the developed model, finding a good correspondence. On the contrary, the prediction performed on the basis of a simplified model consisting of horizontal flat layers significantly underestimates these parameters. From the snapshots of the numerically evaluated seismic wavefield, we could understand that the long duration of the ground motion is due to surface wave overtones originated by the post-critical upward reflection on the sloping interfaces of the uppermost structural units of the S wave reflected from the surface above the top of the ridge generated by the Ferrara folds. Recently, the Rayleigh wave overtones were found to be responsible for the long duration of ground motion in the Valley of Mexico (Cruz-Atienza et al., 2016). Here, we found that areas in the Po Valley could exhibit a similar phenomenon, with the remarkable difference that the surface waves in the Valley of Mexico are excited by the basin edges, whereas in the Po Valley they are generated by a buried structural ridge.
Some persisting inconsistencies between the predicted and observed data can be attributed to local errors in the 3-D model as well as to errors in the assumed source parameterization for the simulated earthquakes. Additional data from more recent and/or still ongoing studies in the area (e.g., Mirandola borehole by Laurenzano et al., 2017) could allow us to improve the model. The performed tests nevertheless represent an encouraging step towards a deeper understanding of the seismic hazard in the Po Plain and in similar alluvial valleys worldwide.
The digital 3-D geological model was set up with the commercial GeoModeller 3.3 software (https://www.intrepid-geophysics.com; Intrepid Geophysics, 2019). The numerical simulations of seismic wave propagation were performed with HPC software developed at Istituto Nazionale di Oceanografia e di Geofisica Sperimentale (OGS) and available from the corresponding author upon request.
The ER3D model in GeoModeller format is available on the Open Science Framework (https://osf.io; Open Science Framework, 2019) at the ER3D project repository (https://doi.org/10.17605/OSF.IO/G7PKR; Klin, 2019). The seismic recordings of the 2012 Emilia sequence events can be downloaded from the Italian Accelerometric Archive – ITACA (2019, http://itaca.mi.ingv.it).
The snapshots of the simulated wavefield in Fig. 11 are taken from a motion picture, which is available on the Open Science Framework (https://osf.io) at the ER3D project repository (https://doi.org/10.17605/OSF.IO/G7PKR, Klin, 2019).
The supplement related to this article is available online at: https://doi.org/10.5194/se-10-931-2019-supplement.
LM conceived the work and selected the relevant geological data for the model construction; EP coordinated the project activities. GL and MAR assembled the digital 3-D geological model; PK performed the numerical predictions.
The authors declare that they have no conflict of interest.
The present work was accomplished under the project “Modellazioni numeriche 3-D per il calcolo del moto del suolo e della risposta sismica in Emilia-Romagna”, funded by Regione Emilia-Romagna. Additional support was provided by the program HPC Training and Research for Earth Sciences (HPC-TRES) (http://www.ogs.trieste.it/en/content/hpc-training-and-research-earth-sciences-hpc-tres, last access: 27 May 2019). The authors thank the anonymous reviewers for their helpful comments and suggestions.
This paper was edited by Irene Bianchi and reviewed by two anonymous referees.
Arias, A.: Seismic Design for Nuclear Power Plants, edited by: Hansen, R. J., Measure of earthquake intensity, Massachusetts Inst. of Tech. Press, 438–483, 1970. a
Barani, S., Albarello, D., Massa, M., and Spallarossa, D.: Influence of twenty years of research on ground-motion prediction equations on probabilistic seismic hazard in Italy, B. Seismol. Soc. Am., 107, 240–255, https://doi.org/10.1785/0120150276, 2017a. a
Barani, S., Albarello, D., Spallarossa, D., and Massa, M.: Empirical scoring of ground motion prediction equations for probabilistic seismic hazard analysis in Italy including site effects, Bull. Earth. Eng., 15, 2547–2570, https://doi.org/10.1007/s10518-016-0040-3, 2017b. a
Barnaba, C., Laurenzano, G., Moratto, L., Sugan, M., Vuan, A., Priolo, E., Romanelli, M., and Di Bartolomeo, P.: Strong-motion observations from the OGS temporary seismic network during the 2012 Emilia sequence in northern Italy, Bull. Earth. Eng., 12, 2165–2178, https://doi.org/10.1007/s10518-014-9610-4, 2014. a
Boccaletti, M., Coli, M., Eva, C., anf G. Giglia, G. F., Lazzarotto, A., Merlanti, F., Nicolich, R., Papani, G., and Postpischl, D.: Considerations on the seismotectonics of the Northern Apennines, Tectonophysics, 117, 7–38, 1985. a, b
Boccaletti, M., Bonini, M., Corti, G., Gasperini, P., Martelli, L., Piccardi, L., Tanini, C., and Vannucci, G.: Seismotectonic Map of the Emilia–Romagna Region in Scale , With Explanatory Notes, CD–ROM, regione Emilia-Romagna, Servizio Geologico Sismico e dei Suoli, CNR – Istituto di Geoscienze e Georisorse Sezione di Firenze, 2004. a, b, c, d, e, f, g, h
Boccaletti, M., Corti, G., and Martelli, L.: Recent and active tectonics of the external zone of the Northern Apennines (Italy), Int. J. Earth Sci., 100, 1331–1348, https://doi.org/10.1007/s00531-010-0545-y, 2011. a, b, c
Brocher, T. M.: Empirical Relations between Elastic Wavespeeds and Density in the Earth's Crust, B. Seismol. Soc. Am., 95, 2081–2092, https://doi.org/10.1785/0120050077, 2005. a
Burrato, P., Ciucci, F., and Valensise, G.: An inventory of the river anomalies in the Po Plain, Northern Italy: evidence for active blind thrust faulting, Ann. Geophys., 46, 865–882, 2003. a
Calcagno, P.: 3D GeoModelling for a Democratic Geothermal Interpretation, in: Proceedings World Geothermal Congress 2015, Melbourne, Australia, 19–25 April 2015, 2015. a
Calcagno, P., Courrioux, G., Guillen, A., Fitzgerald, D., and Mcinerney, P.: How 3D implicit geometric modelling helps to understand geology: The 3Dgeomodeller methodology, in: IAMG 2006 – 11th International Congress for Mathematical Geology: Quantitative Geology from Multiple Sources, 2006. a
Calcagno, P., Chilès, J., Courrioux, G., and Guillen, A.: Geological modelling from field data and geological knowledge. Part I. Modelling method coupling 3D potential-field interpolation and geological rules, Phys. Earth Planet. In., 171, 147–157, https://doi.org/10.1016/j.pepi.2008.06.013, 2008. a, b
Castro, R., Pacor, F., Puglia, R., Ameri, G., Letort, J., Massa, M., and Luzi, L.: The 2012 may 20 and 29, Emilia earthquakes (Northern Italy) and the main aftershocks: S-wave attenuation, acceleration source functions and site effects, Geophys. J. Int., 195, 597–611, https://doi.org/10.1093/gji/ggt245, 2013. a
Chaljub, E., Maufroy, E., Moczo, P., Kristek, J., Hollender, F., Bard, P.-Y., Priolo, E., Klin, P., de Martin, F., Zhang, Z., Zhang, W., and Chen, X.: 3-D numerical simulations of earthquake ground motion in sedimentary basins: testing accuracy through stringent models, Geophys. J. Int., 201, 90–111, https://doi.org/10.1093/gji/ggu472, 2015. a, b
Chilès, J., Aug, C., Guillen, A., and Lees, T.: Modelling the Geometry of Geological Units and its Uncertainty in 3D From Structural Data: The Potential–Field Method, in: Proceedings of Orebody Modelling and Strategic Mine Planning, 313–320, AusIMM, Perth, WA, 2004. a
CNR: Structural Model of Italy, , Quaderni La Ricerca Scientifica n. 114, CNR – Prog. Fin. Geodin. S.P. 5, 1992. a
Cruz-Atienza, V. M., Tago, J., Sanabria-Gómez, J. D., Chaljub, E., Etienne, V., Virieux, J., and Quintanar, L.: Long Duration of Ground Motion in the Paradigmatic Valley of Mexico, Scientific Reports, 6, 38807, https://doi.org/10.1038/srep38807, 2016. a, b
De Nardis, R., Filippi, L., Costa, G., Suhadolc, P., Nicoletti, M., and Lavecchia, G.: Strong motion recorded during the Emilia 2012 thrust earthquakes (Northern Italy): A comprehensive analysis, Bull. Earth. Eng., 12, 2117–2145, 2014. a
Di Dio, G. (Ed.): Riserve idriche sotterranee della Regione Emilia-Romagna, Regione Emilia–Romagna – ENI Agip, Divisione Esplorazione e Produzione, S.EL.CA., Florence, 1998 (in Italian). a
DISS Working Group: Database of Individual Seismogenic Sources (DISS), Version 3.2.1: A compilation of potential sources for earthquakes larger than M 5.5 in Italy and surrounding areas, available at: http://diss.rm.ingv.it/diss/ (last access: 27 May 2019), istituto Nazionale di Geofisica e Vulcanologia, 2018. a, b
Dondi, L., Mostardini, F., and Rizzini, A.: Evoluzione sedimentaria e paleogeografica nella Pianura Padana, Guide Geologiche Regionali, Soc. Geol. Ital., edited by: Cremonini, G. and Ricci Lucchi, F., 47–58, 1982 (in Italian). a
Fantoni, R. and Franciosi, R.: Tectono-sedimentary setting of the Po Plain and Adriatic foreland, Rend. Fis. Acc. Lincei, 21, 197–209, https://doi.org/10.1007/s12210-010-0102-4, 2010. a
Fischer, T., Naumov, D., Sattler, S., Kolditz, O., and Walther, M.: GO2OGS 1.0: a versatile workflow to integrate complex geological information with fault data into numerical simulation models, Geosci. Model Dev., 8, 3681–3694, https://doi.org/10.5194/gmd-8-3681-2015, 2015. a
Fornberg, B.: The pseudospectral method: Comparisons with finite differences for the elastic wave equation, Geophysics, 52, 483–501, 1987. a
Gardner, G. H. F., Gardner, L. W., and Gregory, A. R.: Formation velocity and density; the diagnostic basics for stratigraphic traps, Geophysics, 39, 770–780, https://doi.org/10.1190/1.1440465, 1974. a
Grelle, G., Bonito, L., Lampasi, A., Revellino, P., Guerriero, L., Sappa, G., and Guadagno, F. M.: SiSeRHMap v1.0: a simulator for mapped seismic response using a hybrid model, Geosci. Model Dev., 9, 1567–1596, 2016. a
Guillen, A., Courrioux, G., Calcagno, P., Lane, R., Lees, T., and McInerney, P.: Constrained gravity 3D litho-inversion applied to Broken Hill, ASEG Extended Abstracts, 2004, 1–6, https://doi.org/10.1071/ASEG2004ab057, 2004. a
Herrmann, R.: Computer programs in seismology: An evolving tool for instruction and research, Seismol. Res. Lett., 84, 1081–1088, https://doi.org/10.1785/0220110096, 2013. a
Intrepid Geophysics: https://www.intrepid-geophysics.com, last access: 27 May 2019. a
ITACA: http://itaca.mi.ingv.it, last access: 27 May 2019. a, b
Klin, P.: ER3D: Structural and geophysical 3D model of central Emilia-Romagna, public project on the Open Science Framework, https://doi.org/10.17605/OSF.IO/G7PKR, 2019. a, b, c
Klin, P., Priolo, E., and Seriani, G.: Numerical simulation of seismic wave propagation in realistic 3-D geo-models with a Fourier pseudo-spectral method, Geophys. J. Int., 183, 905–922, 2010. a, b
Komatitsch, D. and Martin, R.: An unsplit convolutional perfectly matched layer improved at grazing incidence for the seismic wave equation, Geophysics, 72, SM155–SM167, 2007. a
Kreiss, H.-O. and Oliger, J.: Comparison of accurate methods for the integration of hyperbolic equations, Tellus, 24, 199–215, 1972. a
Lajaunie, C., Courrioux, G., and Manuel, L.: Foliation fields and 3D cartography in geology: Principles of a method based on potential interpolation, Math. Geol., 29, 571–583, 1997. a
Laurenzano, G., Priolo, E., Mucciarelli, M., Martelli, L., and Romanelli, M.: Site response estimation at Mirandola by virtual reference station, Bull. Earth. Eng., 15, 2393–2409, https://doi.org/10.1007/s10518-016-0037-y, 2017. a, b
Lavecchia, G., de Nardis, R., Costa, G., Tiberi, L., Ferrarini, F., Cirillo, D., Brozzetti, F., and Suhadolc, P.: Was the Mirandola thrust really involved in the Emilia 2012 seismic sequence (northern Italy)? Implications on the likelihood of triggered seismicity effects, B. Geofis. Teor. Appl., 56, 461–488, https://doi.org/10.4430/bgta0162, 2015. a
Luzi, L., Pacor, F., Ameri, G., Puglia, R., Burrato, P., Massa, M., Augliera, P., Franceschina, G., Lovati, S., and Castro, R.: Overview on the Strong-Motion Data Recorded during the May-June 2012 Emilia Seismic Sequence, Seismol. Res. Lett., 84, 629–644, https://doi.org/10.1785/0220120154, 2013. a
Malagnini, L., Herrmann, R. B., Munafò, I., Buttinelli, M., Anselmi, M., Akinci, A., and Boschi, E.: The 2012 Ferrara seismic sequence: Regional crustal structure, earthquake sources, and seismic hazard, Geophys. Res. Lett., 39, L19302, https://doi.org/10.1029/2012GL053214, 2012. a, b
Mallet, J.-L. L.: Geomodeling, Oxford University Press, Inc., New York, NY, USA, 2002. a, b
Martelli, L., Bonini, M., Calabrese, L., Corti, G., Ercolessi, G., Molinari, F. C., Piccardi, L., Pondrelli, S., and Sani, F.: Seismotectonics map of the Emilia-Romagna Region and surrounding areas, scale, available at: http://ambiente.regione.emilia-romagna.it/it/geologia/pubblicazioni/cartografia-geo-tematica/carta- sismotettonica-della-regione-emilia-romagna-e-aree-limitrofe-edizione-2016 (last access: 27 May 2019), regione Emilia-Romagna, Servizio Geologico Sismico e dei Suoli, 2017. a, b, c, d
Maufroy, E., Chaljub, E., Hollender, F., Kristek, J., Moczo, P., Klin, P., Priolo, E., Iwaki, A., Iwata, T., Etienne, V., De Martin, F., Theodoulidis, N. P., Manakou, M., Guyonnet-Benaize, C., Pitilakis, K., and Bard, P.-Y.: Earthquake Ground Motion in the Mygdonian Basin, Greece: The E2VP Verification and Validation of 3D Numerical Simulation up to 4 Hz, B. Seismol. Soc. Am., 105, 1398–1418, 2015. a, b, c
McInerney, P., Guillen, A., Courrioux, G., Calcagno, P., and Lees, T.: Building 3D Geological Models Directly from the Data? A new approach applied to Broken Hill, Australia, in: Digital Mapping Techniques '05 – Workshop Proceedings, Baton Rouge, Louisiana, 2005. a
Milana, G., Bordoni, P., Cara, F., Di Giulio, G., Hailemikael, S., and Rovelli, A.: 1D velocity structure of the Po River plain (Northern Italy) assessed by combining strong motion and ambient noise data, B. Earthq. Eng., 12, 2195–2209, https://doi.org/10.1007/s10518-013-9483-y, 2014. a
Moczo, P., Kristek, J., Vavryčuk, V., Archuleta, R. J., and Halada, L.: 3D Heterogeneous Staggered-Grid Finite-Difference Modeling of Seismic Motion with Volume Harmonic and Arithmetic Averaging of Elastic Moduli and Densities, B. Seismol. Soc. Am., 92, 3042–3066, 2002. a
Moczo, P., Kristek, J., and Gális, M.: The Finite-Difference Modelling of Earthquake Motions. Waves and Ruptures, Cambridge University Press, Cambridge, United Kingdom, 2014. a
Molinari, I., Argnani, A., Morelli, A., and Basini, P.: Development and testing of a 3D seismic velocity model of the Po Plain sedimentary basin, Italy, B. Seismol. Soc. Am., 105, 753–764, 2015. a, b
Montone, P. and Mariucci, M. T.: P-wave Velocity, Density, and Vertical Stress Magnitude Along the Crustal Po Plain (Northern Italy) from Sonic Log Drilling Data, Pure Appl. Geophys., 172, 1547–1561, https://doi.org/10.1007/s00024-014-1022-5, 2015. a
Morozov, I.: On the relation between bulk and shear seismic dissipation, B. Seismol. Soc. Am., 105, 3180–3188, https://doi.org/10.1785/0120150093, 2015. a
Open Science Framework: https://osf.io, last access: 27 May 2019. a
Pacor, F., Paolucci, R., Luzi, L., Sabetta, F., Spinelli, A., Gorini, A., Nicoletti, M., Marcucci, S., Filippi, L., and Dolce, M.: Overview of the Italian strong motion database ITACA 1.0, Bull. Earth. Eng., 9, 1723–1739, 2011. a
Paolucci, R., Smerzini, C., and Mazzieri, I.: Anatomy of strong ground motion: near-source records and three-dimensional physics-based numerical simulations of the Mw 6.0 2012 May 29 Po Plain earthquake, Italy, Geophys. J. Int., 203, 2001–2020, 2015. a, b, c, d, e
Pieri, M. and Groppi, G.: Subsurface Geological Structures of the Po Plain, Publication 414, CNR, progetto Finalizzato Geodinamica, 1981. a, b, c, d, e
Pondrelli, S., Salimbeni, S., Ekström, G., Morelli, A., Gasperini, P., and Vannucci, G.: The Italian CMT dataset from 1977 to the present, Phys. Earth Planet. In., 159, 286–303, https://doi.org/10.1016/j.pepi.2006.07.008, 2006. a
Priolo, E., Romanelli, M., Barnaba, C., Mucciarelli, M., Laurenzano, G., Dall'Olio, L., Abu Zeid, N., Caputo, R., Santarato, G., Vignola, L., Lizza, C., and Di Bartolomeo, P.: The Ferrara thrust earthquakes of May–June 2012: Preliminary site response analysis at the sites of the OGS temporary network, Ann. Geophys., 55, 591–597, 2012. a, b
Rovida, A., Locati, M., Camassi, R., Lolli, B., and Gasperini, P.: CPTI15, the 2015 version of the Parametric Catalogue of Italian Earthquakes, https://doi.org/10.6092/INGV.IT-CPTI15, istituto Nazionale di Geofisica e Vulcanologia, 2016. a, b, c
Saraò, A. and Peruzza, L.: Fault-plane solutions from moment-tensor inversion and preliminary Coulomb stress analysis for the Emilia Plain, Ann. Geophys., 55, 647–654, https://doi.org/10.4401/ag-6134, 2012. a
Taborda, R. and Roten, D.: Physics-Based Ground-Motion Simulation, in: Encyclopedia of Earthquake Engineering, Springer-Verlag, Berlin Heidelberg, 2015. a
Turrini, C., Lacombe, O., and Roure, F.: Present-day 3D structural model of the Po Valley basin, Northern Italy, Mar. Petrol. Geol., 56, 266–289, 2014. a
Vuan, A., Klin, P., Laurenzano, G., and Priolo, E.: Far-source longperiod displacement response spectra in the Po and Venetian Plains (Italy) from 3D wavefield simulations, B. Seismol. Soc. Am., 101, 1055–1072, 2011. a
- Abstract
- Introduction
- The structural and geophysical 3-D model of central Emilia
- Computation of seismic waves
- Comparisons between numerical predictions and data
- Conclusions
- Code availability
- Data availability
- Video supplement
- Author contributions
- Competing interests
- Acknowledgements
- Review statement
- References
- Supplement
- Abstract
- Introduction
- The structural and geophysical 3-D model of central Emilia
- Computation of seismic waves
- Comparisons between numerical predictions and data
- Conclusions
- Code availability
- Data availability
- Video supplement
- Author contributions
- Competing interests
- Acknowledgements
- Review statement
- References
- Supplement