the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A multi-phasic approach for estimating the Biot coefficient for Grimsel granite
Patrick Selvadurai
Paul A. Selvadurai
Morteza Nejati
This paper presents an alternative approach for estimating the Biot coefficient for the Grimsel granite, which appeals to the multi-phasic mineralogical composition of the rock. The modelling considers the transversely isotropic nature of the rock that is evident from both the visual appearance of the rock and determined from mechanical testing. Conventionally, estimation of the compressibility of the solid material is performed by fluid saturation of the pore space and pressurization. The drawback of this approach in terms of complicated experimentation and influences of the unsaturated pore space is alleviated by adopting the methods for estimating the solid material compressibility using developments in theories of multi-phase materials. The results of the proposed approach are compared with estimates available in the literature.
- Article
(3807 KB) - Full-text XML
- BibTeX
- EndNote
The classical theory of poroelasticity proposed by Biot (1941) is a major contribution to the disciplines of geosciences and geomechanics with applications that include porous earth materials saturated by fluids. The studies in this area are numerous and no attempt will be made to provide a comprehensive survey of past and recent developments. Advances in the area of poroelasticity and its applications to problems in geomechanics in particular are given by Yue and Selvadurai (1995), Selvadurai (1996), Selvadurai (2007), Wang (2000), Verruijt (2015), Cheng (2015), Selvadurai et al. (2015), Selvadurai and Suvorov (2016), and others. The basic development of the classical theory of poroelasticity relies on constitutive assumptions of Hookean elastic behaviour of the porous skeleton and Darcy flow through the porous medium. In addition, an important component of the theory relates to the partitioning of the total stress tensor for the poroelastic solid between the stresses carried purely by the porous skeleton and the stresses carried by the pore fluid. The partitioning is an important component in the theory of poroelasticity that allows the time-dependent shedding of the applied stresses from the pore fluid to the porous skeleton. The stresses sustained by the porous skeleton have important consequences for the definition of failure of the poroelastic material either through the development of damage (Selvadurai, 2004; Selvadurai and Shirazi, 2004, 2005; Selvadurai et al., 2015) or fracture development and boundary effects on heterogeneities (Selvadurai et al., 2011; Selvadurai and Głowacki, 2017, 2018) or plastic flow (Selvadurai and Suvorov, 2012, 2014). From an environmental geosciences perspective, alterations in the skeletal permeability associated with its damage can lead to enhanced migration of contaminants and hazardous materials. In Biot's theory, the partitioning of the total stress is achieved through consideration of the bulk modulus of the porous skeleton (KD) and the bulk modulus of the solid material composing the porous skeleton (KS), which introduces the Biot coefficient α and, for an isotropic elastic skeleton, has the form . When the bulk modulus of the solid material is large in comparison to the skeletal bulk modulus, α→0, which is the conventional stress partitioning approach proposed in the theory of soil consolidation proposed by Terzaghi (1923). Unlike in soils, the Biot coefficient for rocks can be less than unity. If Biot's classical theory of poroelasticity is accepted, values of α cannot be greater than unity. Such a value would imply that either KD<0 or KS<0, which would violate the positive definiteness arguments for the strain energy of an elastic porous skeleton (Davis and Selvadurai, 1996; Selvadurai, 2000) with no locked-in self equilibrating stresses (i.e. the skeleton expands under compressive isotropic stresses). A range of values for α is given by Detournay and Cheng (1993), Wang (2000), and Cheng (2015).
The experimental procedure for determining the Biot coefficient α involves estimating the bulk modulus of the porous skeleton (KD), which, in the case of an isotropic skeletal fabric, can be obtained by subjecting a dry or moisture free and jacketed specimen of the rock to isotropic compression and measuring the resulting volumetric strain. This is a straightforward experimental technique and the results can also be verified by conducting uniaxial compression tests on the isotropic rock and measuring both the Young's modulus and Poisson's ratio. The measurement of the compressibility of the solid material composing the skeletal fabric can be either straightforward or complicated depending on the permeability characteristics of the porous material. For rocks with relatively high permeability (e.g. Indiana limestone – Selvadurai and Glowacki, 2008 and Selvadurai and Selvadurai, 2010, 2014; Vosges sandstone – Moulu et al., 1997), the pore space of the rock can be saturated by initiating a combination of steady flow and vacuum saturation. To determine the compressibility of the solid material, the confining isotropic stresses are allowed to nearly equilibrate with the pore fluid pressure and the volume changes measured can be used to estimate the compressibility of the solid material composing the porous fabric. With very low-permeability materials (e.g. the Cobourg limestone to 10−19 m2, Selvadurai et al., 2011), the process of saturation of the pore space can take an inordinately long time with no assurance that the entire pore space is fully saturated or that there are no residual pore fluid pressure artefacts (Selvadurai, 2009). Furthermore, even if the pore space is saturated, attaining equalization of the externally applied pressure with the internal pore fluid pressure can take substantial time (for 150 mm diameter cylindrical Cobourg limestone samples, more than 100 d are required for saturation). For this reason, Selvadurai (2019) proposed an alternative approach where the compressibility of the solid material phase(s) can be estimated by considering the multi-phasic theories developed for estimating the effective properties of composite elastic materials. The composite material theories associated with the Voigt–Reuss–Hill estimates (Voigt, 1928; Reuss, 1929; Hill, 1952, 1965) and the upper and lower bound estimates proposed by Hashin and Shtrikman (1963) can be used to estimate the bulk modulus of the solid material (see also Walpole, 1966, and Francfort and Murat, 1986). In this paper, we apply these basic concepts to determine the Biot coefficient for the Grimsel granite. This granite is encountered in the Underground Research Laboratory constructed in Grimsel, Switzerland, in order to perform heater experiments to simulate the thermo-hydro-mechanical (THM) loading associated with heat-emitting containers in the event that the site is chosen as a repository for the deep geologic disposal of high-level nuclear fuel waste (i.e. the Full-scale Engineered Barriers EXperiment (FEBEX)). A typical section along the Grimsel Laboratory associated with the FEBEX heater experiment location is shown in Fig. 1.
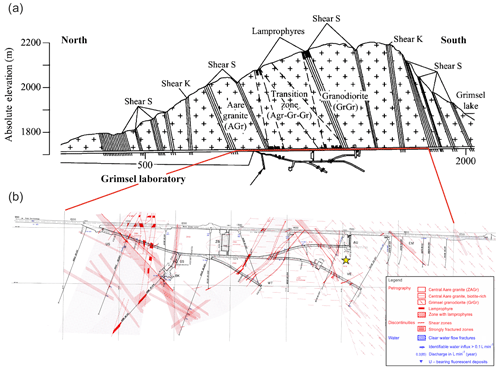
Figure 1(a) The Grimsel Laboratory and the FEBEX Drift (after Alonso et al., 2005); (b) detailed map view of the FEBEX drift for reference only (After Keusen et al., 1989 and from NAGRA Technical Report NTB87-14E).
The Aar granitic rock (also referred to as Aare granitic rock) setting at Grimsel has been associated with initiatives related to the use of granitic rock formations as potential hosts for the creation of deep geologic repositories for the disposal of heat-emitting nuclear fuel waste. Detailed descriptions of the geological settings of the Aar Massif of the Central Alps are given by several authors including Stalder (1964), Wüthrich (1965), Steck and Burri (1971), Schaltegger (1990a), Schaltegger (1990b), and Schaltegger and Corfu (1992), and references to further studies are given by Goncalves et al. (2012). Geoscientific studies of the Aar granite have been conducted by a number of agencies including NAGRA (Nationale Genossenschaft für die Lagerung radioaktiver Abfälle) and ENRESA (Empresa Nacional de Residuos Radiactivos, S.A.), and these initiatives are documented in several reports and articles by Amiguet (1985), Pahl et al. (1989), Keusen et al. (1989), Möri et al. (2003), Alonso and Alcoverro (2005), Alonso et al. (2005), Rabung et al. (2012), Bouffier (2015), Garralón et al. (2017), and Krietsch et al. (2019). In relation to the FEBEX research experiments, the geological setting of the Grimsel Laboratory contains alternate layers of the Aar granite, transition zones, and Granodiorite, separated by Lamprophyres and zones that are subjected to intense shearing. A typical view of the geological setting is shown in Fig. 1. During the FEBEX experiments, the Grimsel Laboratory was used to conduct heater experiments, where the heaters were encapsulated in bentonitic clay. An extensive programme of research was conducted by a series of research groups to validate the THM response of both the bentonitic buffer and the rock mass and the results of the research efforts are documented by Alonso and Alcoverro (2005) and Alonso et al. (2005). The Grimsel granite used in this research investigation was obtained from boreholes PRP16.001 and INJ16.001 located in the southern part of the laboratory, drilled from a cavern located at a depth of approximately 450 m. These boreholes were drilled as a part of the Grimsel In situ Stimulation and Circulation (ISC) project (see the location in Fig. 1) that investigated the seismo-hydro-mechanical response of the rock mass to hydraulic stimulation (Amann et al., 2018; Gischig et al., 2018; Doetsch et al., 2018; Jalali et al., 2018).
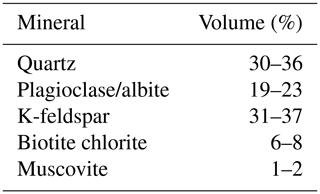
During the geological evolution of the Aar Massif, the strata acquired different mineralogical compositions, and the studies by Schaltegger and Krähenbühl (1990) contain very detailed evaluations of the mineralogical compositions of rocks recovered from the Grimsel and Reuss regions. This information is valuable for estimating the solid material compressibility of the Grimsel granite and for distinguishing the sample locations. For example, the work of Jokelainen et al. (2013) provides information on the mineralogical composition of the Grimsel granodiorite, and the study by Missana and Garcia-Gutiérrez (2012) provides the mineralogical composition of the FEBEX granite. The results reported in these investigations are summarized in Tables 1–4 for completeness.
Table 1Short petrographical descriptions of the rock samples analysed by Schaltegger and Krähenbühl (1990). Compositions are estimated from thin section; all – allanite; ap – apatite; bio – biotite; cc – calcite; chl – chlorite; ep – epidote; fluo – fluorite; gar – garnet; kfs – K-feldspar; leuc – leucoxene; op – opaques; plag – plagioclase; ser – sericite; sph – sphene; stilp – stilpnomelane; qtz – quartz; zir – zircon. The Central Aar granite s.s refers to granitic rocks sampled within the Aar valley, whereas the Central Aar s.l. refers to samples from the same geological unit but that were sampled in the Reuss valley, which is the valley to the east of the Aar valley.
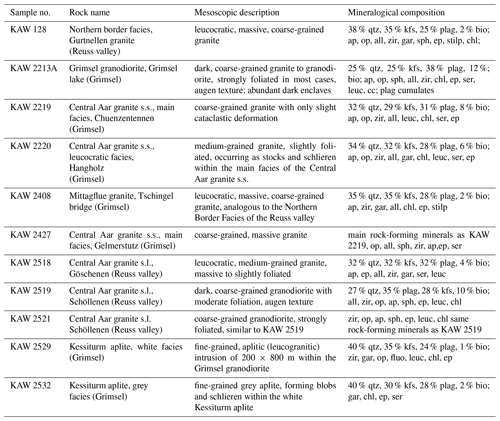
Table 2Geochemical descriptions of the rock samples across the Grimsel test site given by Keusen et al. (1989).
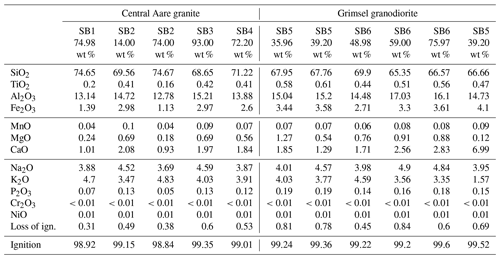
Figure 2 shows cores of the Grimsel granite and, from a visual perspective, the rock has the appearance of stratifications that would point to the likely presence of transverse isotropy, in terms of its elasticity properties, fluid flow, and fracture and failure characteristics.
The microstructure includes larger crystals of quartz (with dimensions of up to 8 mm), and this requires that a suitable representative volume element is considered, both in the mechanical testing and mineralogical property evaluations. Extensive geomechanical characterization studies have been performed on the Grimsel granite, and these are given in the references cited previously. Permeability studies are also reported by Schild et al. (2001). A comprehensive inter-laboratory study of permeability of the Grimsel granodiorite is also given in David et al. (2018a, b).
The objective of this study is to employ the existing data on the mechanical characterization of the transversely isotropic granite to estimate the skeletal compressibility of the granite and to use XRD (X-ray diffraction) studies of the mineralogical composition of the Grimsel granite to estimate the compressibility of the solid phase composing the porous fabric.
The fabric of the Grimsel granite is indicative of a transversely isotropic material (Nejati, 2018; Dutler et al., 2018; Dambly et al., 2019; Nejati et al., 2019). The elastic stress–strain relationships for a transversely isotropic material can be expressed in several forms (see, e.g., Hearmon, 1961, Lekhnitskii, 1963, and Ting, 1996). We consider the case where the plane of isotropy (x,y) of the transversely isotropic elastic material is normal to the z axis. The equations of elasticity governing the normal strains can be written in the forms
We point out that the Poisson's ratio is generally defined as for a stress in the i direction. From Betti's reciprocal theorem
Due to the isotropic behaviour in the xy plane, Ex=Ey, and νzy=νzx. These relations reduce the independent material constants needed to define the principal strains to four: Ex, Ez, νxy, and νzx. Consider the situation where an element of the transversely isotropic elastic medium is subjected to an isotropic compressive stress state: . The infinitesimal volumetric strain
The skeletal bulk modulus for the transversely isotropic elastic material can be expressed in the form
In terms of the elasticity parameters that are applicable to the direction normal to the planes of stratification (N) and directions along the planes of foliation or stratification (T), Eq. (4) can be written as
In the limit of material isotropy, and and Eq. (5) reduces to the classical result
The estimation of the skeletal bulk modulus of the Grimsel granite can be attempted provided that the elasticity constants applicable to either an isotropic fabric or a transversely isotropic skeletal elastic behaviour can be identified. The geomechanical investigations of the granitic rocks at Grimsel have ranged from the estimation of the deformability and strength characteristics of the rock to the assessment of the in situ stress state. The interpretation of the available data for estimating the skeletal deformability characteristics is complicated by the fact that the approaches used are not uniform and standardized; the earlier experimental studies may have deviated from currently acceptable standards (as suggested by ASTM (American Society for Testing and Materials) and ISRM (The International Society for Rock Mechanics)) for sample size, rate of loading, end restraints, method of interpretation of the experimental data for parameter extraction (secant modulus, tangent modulus, loading/unloading paths, cycles), etc. The exercise is also compounded by the material variability in terms of the Grimsel lithology and its influence on parameter variability. Within these limitations, attempts can be made to extract, from the existing literature, representative values of the elasticity characteristics of Grimsel granite with due consideration for the species of granite. The earliest record used in this study relates to the work of Amiguet (1985) and Alonso and Alcoverro (2005), which indicate the elasticity properties as E≈60 GPa, ν≈0.25.
Table 3Mineralogical composition of the Grimsel granodiorite (Gr-Gr) (After Jokelainen et al., 2013).
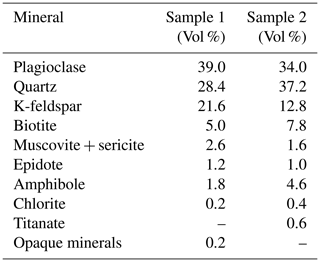
Table 4Mineralogical composition of the FEBEX granite (after Missana and Garcia-Gutiérrez, 2012).
Pahl et al. (1989) used borehole dilatometer and overcoring to estimate the in situ stress state and the overall deformability characteristics of the granite: E≈40 GPa, ν≈0.25. The work of Keusen et al. (1989) gives a range of elasticity values applicable to the granodiorite (max[E≈63 GPa, ν≈0.48]; min[E≈32 GPa, ν≈0.18]) and the Aar granite (max[E≈64 GPa, ν≈0.49]; min[E≈42 GPa, ν≈0.25]). Ziegler and Amann (2012) also report the results of an extensive series of tests conducted on both wet and dry and coarse-grained and fine-grained samples of Grimsel granite. The results are presented as maximum and minimum values as follows: coarse-grained granite: max[E≈59 GPa, ν≈0.37], min[E≈53 GPa, ν≈0.25]; medium-grained granite: max[E≈63 GPa, ν≈0.41], min[E≈52 GPa, ν≈0.17]. The recent work of Bouffier (2015) uses laboratory overcoring techniques to estimate the deformability characteristics of the Grimsel granite, and there is a wide range of results for both the elastic modulus and Poisson's ratio; average representative results are indicated by E≈25 GPa, ν≈0.33. The work of Kant et al. (2017) is primarily focused on the estimation of the thermal properties of the Aar granite. The results they cite for the modulus of elasticity and Poisson's ratio are directly obtained from the work of Alonso et al. (2005) or indirectly from Keusen et al. (1989). Wenning et al. (2018) report studies of permeability and seismic velocity anisotropy across a ductile to brittle transition zone in the Grimsel granite.
The skeletal compressibility is also an important parameter in the interpretation of transient hydraulic pulse tests for estimating the fluid transport properties of low-permeability materials including granite and argillaceous limestones (Brace et al., 1968; Selvadurai and Carnaffan, 1997; Selvadurai and Selvadurai, 2014; Selvadurai and Najari, 2015). The elasticity properties were determined via dynamic measurements and the maximum and minimum values are as follows: max[E≈95 GPa, ν≈0.18], min[E≈65 GPa, ν≈0.15]. Considering the nature of the ductile to brittle transmission zone under investigation and the dynamic nature of the tests, these estimates are far in excess of those for the intact material that is tested statically. Furthermore, the bulk modulus estimated from the maximum values of E and ν is in the range of 50 GPa, which is lower than the bulk modulus of mono-mineralic albite but exceeds that of quartz. The study by Krietsch et al. (2019) deals with the characterization of the in situ stress state at the Grimsel test site, using a range of experiments including overcoring and hydraulic fracturing. The investigations were extended to include transverse isotropy of the rock mass.
The elasticity parameters were inferred through a computational back analysis of the overcoring technique; these authors also provide a comparison with the results obtained by Bouffier (2015). An averaging procedure gives maximum estimates of the isotropic elasticity parameters as E≈26 GPa, ν≈0.33. The use of the Grimsel Laboratory facility for the FEBEX experiment (Alonso and Alcoverro, 2005) provided a useful international benchmarking exercise to validate THM modelling of clay buffer regions that could be used in high-level nuclear waste management endeavours. The international collaborative effort (Alonso et al., 2005) focused more on the behaviour of the clay barrier during heating from emplaced heaters and fluid influx from the Grimsel granite. In many of the research efforts for the FEBEX Project, the Grimsel granite served as a heat sink and the rock mechanics aspects perhaps received less emphasis (i.e. the modelling of the bentonitic clay under heating was considered to be the major objective of the research as opposed to the modelling of the Grimsel granite). Also, to enhance fluid influx, the Grimsel gallery was considered to be a fractured rock mass, and modelling the Grimsel rock elasticity properties varied between the research groups participating in the FEBEX project, with very low estimates of the elasticity properties (Nguyen et al., 2005) to near-intact rock properties derived from the original studies of Amiguet (1985) (see also Gens et al., 1998, Alonso and Alcoverro, 2005, Rutqvist et al., 2003, and Dupray et al., 2013). For this reason, the elasticity properties of the Grimsel granite cited in the papers dealing with the FEBEX exercise are excluded from consideration.
The majority of the studies focusing on the evaluation of the deformability characteristics of the Grimsel granite deal with isotropic elastic modelling. The possible influences of either elastic anisotropy or elastic transverse isotropy were addressed in the earlier study by Pahl et al. (1989) in connection with the estimation of in situ stress states. In this particular study, there is no clear statement of the applicable value of the elasticity constants governing transverse isotropy of the Grimsel granite (the degree of anisotropy (ET∕EN) does not exceed 1.25), and the study culminates in the adoption of the isotropic elasticity properties that were indicated previously. The research by Nejati (2018) and Nejati et al. (2019) deals with the estimation of the deformability characteristics of the Grimsel granite based on the transversely isotropic elastic model with principal directions aligned in the stratification planes and normal to the planes (Fig. 2). These studies indicate that the Grimsel granite tested also exhibited significant anisotropy and nonlinearity. In addition, due to nonlinear effects, the secant, tangent, and average values of the Young's modulus can depend on the stress level at which the value is estimated.
If a range of elastic behaviour can be clearly defined and if the elastic constants governing transverse isotropy can be determined, then, as shown by Eq. (5), the bulk modulus applicable to the transversely isotropic material can be evaluated objectively. The studies conducted by Nejati (2018) and Nejati et al. (2019) provide the following estimates for the elastic constants governing the transversely isotropic elasticity model for the Grimsel granite: EN≈30; ET≈47, νTT≈0.20, νNT≈0.10 GPa, Finally, Krietsch et al. (2019) conducted a series of experiments on the ISC core plugs, using overcoring and external pressurization of the hollow samples. These authors also give results of uniaxial tests conducted on core plugs extracted either normal or parallel to the foliations (Fig. 18 of their paper). These results can be used to estimate the EN and ET. From the results presented by Krietsch et al. (2019), the relevant elastic moduli can be summarized as follows: EN≈13; ET≈35 GPa. These investigations, however, cannot be used to estimate the values of νTT and νNT. Dambly et al. (2019) presented the results of a research programme geared to estimate the transversely isotropic elasticity parameters from results of ultrasonic dynamic tests and static tests. Nejati et al. (2019) compared the static and dynamic values of the elastic constants at zero confinement and concluded that the dynamic moduli are significantly greater than the static ones. In this study we have not considered experimental results derived from dynamic testing; therefore, for consistency, any results derived from dynamic testing of the Grimsel granite have been excluded from further consideration. Considering the experimental evaluations available in the literature, the elasticity parameters applicable to the Grimsel granite are summarized in Table 5.
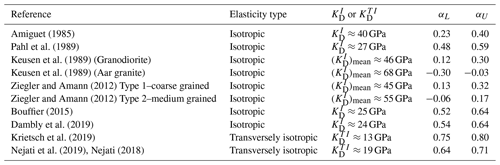
Amiguet (1985)Pahl et al. (1989)Keusen et al. (1989)Keusen et al. (1989)Ziegler and Amann (2012)Ziegler and Amann (2012)Bouffier (2015)Dambly et al. (2019)Krietsch et al. (2019)Nejati et al. (2019)Nejati (2018)Table 5Elasticity properties for the Grimsel granite with the corresponding or values: ; N signifies the direction normal to the planes of stratification and T signifies the directions along the planes of stratification.
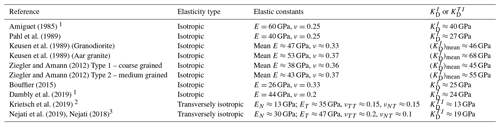
1 This estimate is based on the elastic constants measured along the foliations. 2 This estimate is based on the secant elastic constants at a stress level of approximately 9 MPa. 3 This estimate is based on tangent elastic constants at the in situ stress level based on the analyses of Krietsch et al. (2019), which is approximately 11 MPa.
The skeletal material of the Grimsel granite consists of a variety of mineral phases including quartz, biotite, anorthite, augite, microcline, and traces of pyrite and magnetite. The composition of these minerals was determined both at the XRD facilities at University of Montréal, QC, Canada and at the Department of Earth Sciences, Institute of Geology, ETH, Zurich (Wenning et al., 2018). The estimated volume fractions and the values for the bulk moduli and shear moduli are shown in Tables 6 and 7, respectively. The average volume fractions and the mineralogical compositions tend to vary and the estimated values are, in general, considered to be approximate. The results of the XRD evaluations do not provide sufficient accuracy to group the tested rocks into either the Grimsel granodiorite or the FEBEX Grimsel categories. A very cursory comparison with the data provided in Tables 1 to 3 would suggest that the mineralogical compositions provided by Wenning et al. (2018) and indicated in Table 6 correspond to the Grimsel granodiorite, and the results shown in Table 7 correspond to the FEBEX granite. For this reason, the XRD data derived from both laboratory evaluations (ETH and McGill) are retained in the estimations of the solid material compressibility KS. Also, the void fraction (≪1 %) is neglected in the calculations. The values for the bulk moduli and shear moduli for the various minerals were obtained from published literature (Alexandrov et al., 1964; Anderson and Nafe, 1965; Carmichael, 1990; Sisodia and Verma, 1990; Moos et al., 1997; Redfern and Angel, 1999; Schilling et al., 2003; Zhu et al., 2007; Mavko et al., 2009; Lin, 2013).
Table 6Mineralogical fractions of the Grimsel granite (data obtained by Wenning et al., 2018, Institute of Geology, ETH, Zurich).
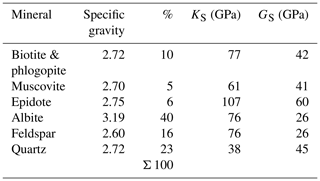
Table 7Mineralogical fractions of the Grimsel granite (data obtained by the Earth Sciences Laboratory, University of Montréal).
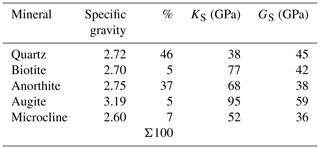
In the multi-phasic approach, the objective is to determine the overall bulk modulus for the solid mineralogical phase by considering the bulk moduli for the separate mineral constituents and their volume fractions. Ideally this needs to be approached using a generalized theory of multi-phasic composites that can accommodate a mixture of any number of phases. Such a generalized theory is yet to be developed. The most widely used relationships are those by Voigt (1928) and Reuss (1929). The Voigt (V) and the Reuss (R) estimates are
where i is quartz, biotite, anorthite, augite, microcline, and voids and subscripts I = 1, 2 refer to the data derived from Table 6 and Table 7, respectively. .
The results given in Hill (1952, 1965) are the mean of the Voigt and Reuss estimates. This basic approach can be applied to estimate the effective bulk and shear moduli for the Grimsel granite: i.e.
where subscripts I=1, 2 refer to the data derived from Tables 6 and 7 respectively.
Using the mineralogical compositions obtained from XRD analyses given in Table 1, we have
and using the mineralogical compositions obtained from XRD analyses given in Table 2, we have
We consider the upper and lower bounds for a multi-phasic composite consisting of n phases developed by Walpole (1966). The effective bulk modulus K for the multi-phasic material can be written as
where
In Eq. (12), Gl and Gg are, respectively, the lowest and greatest values of the shear modulus of the n phases. For completeness, we also record here the bounds for the effective shear modulus (G) of the n phasic mixture, which can be written as
where
and Kl and Kg are, respectively, the lowest and greatest values of the bulk modulus of the n phases.
Considering the multi-phasic data set given in Tables 6 and 7, respectively,
Considering the range of solid material compressibilities obtained from the two laboratory investigations, we can conclude that the lower (L) and upper (U) estimates for KS are approximately
The results for the skeletal compressibilities given in Table 5 can be combined with the range of solid material compressibilities to estimate the upper and lower limits of the Biot coefficient applicable to each estimate of and . The relevant results are shown in Table 8.
Amiguet (1985)Pahl et al. (1989)Keusen et al. (1989)Keusen et al. (1989)Ziegler and Amann (2012)Ziegler and Amann (2012)Bouffier (2015)Dambly et al. (2019)Krietsch et al. (2019)Nejati et al. (2019)Nejati (2018)Pahl et al. (1989)Bouffier (2015)Dambly et al. (2019)Nejati et al. (2019)Nejati (2018)In theories developed for estimating the elasticity of multi-phasic materials, the most extensive studies relate to two-component elastic materials. Theories, however, have also been developed by several researchers to include a distribution of three elastic phases in the composite material. An early study in this area is by Cohen and Ishai (1967) that considered the presence of a large-void content in the two-phase system. Several other developments have been proposed in the literature; references to such studies are given by Ju and Chen (1994a, b) and the references cited in the Introduction. The extension to three elastic phases was also presented in the studies by Talbot et al. (1995) and, more recently, by Lin and Ju (2009). Even with these developments, the number of separate components included in the composite material models are insufficient to accommodate all the components of the solid phases listed in Tables 1 to 3 and 5 and 6.
A plausible alternate approach is to essentially reduce the components in Tables 1 and 2 to three phases by combining (using the Voigt–Reuss–Hill approach) the material phases that correlate closely in terms of their bulk and shear moduli values. Whether, in view of the approximate nature of the XRD evaluations of the volume fractions of the separate phases, such refinements are altogether warranted is debatable. The results of the evaluations presented in the paper suggest that the multi-phasic approach in conjunction with XRD data provides a useful alternative to validating the conventional experimental approach for estimating the solid material composing low-permeability porous media. The skeletal bulk moduli for the Grimsel granite shows a wide variation, indicative of variable lithology of the igneous rock formation. In this sense it is prudent to assume a set of limits for the choice of the Biot coefficient rather than to assign a specific value. Certain data obtained in this study give rise to non-realistic values of the Biot coefficient, clearly arising from the estimation of the skeletal compressibility.
As a guide, experimental results for the skeletal compressibility values that exceed the effective solid material compressibility of the minerals with the largest volume fractions should be disregarded. Therefore these results can be excluded without further comment. (Since the multi-phasic assessment of the compressibility of the solid material has a lower limit of approximately GPa, plausible values of the Biot coefficient will be obtained when KD<KS.) Also, excessively low values of KD need to be re-examined before using the data to estimate the Biot coefficient. Excessively low values can result from inaccurate estimation of the elastic modulus and Poisson's ratio. Similarly, excessively high values of the skeletal stiffness can result from inaccurate estimates of the Poisson's ratio of the rock. For example, if samples are loaded in the direction of the foliations or stratifications, micro-crack or defect development during compression can give rise to lateral deformations that can be a result of void or crack generation and not a result of material deformation. Considering the numerical values presented in Table 8, and the above comments, several estimates for the Biot coefficients can be excluded from further discussion. The Table 9 summarizes the revised set of realistic experimental estimates for the Biot coefficient of the Grimsel granite, taking into consideration the aforementioned caveats on the experimental results.
The accurate estimation of the skeletal deformability characteristics of a porous rock is an essential prerequisite for estimating the Biot coefficient for a fluid-saturated poroelastic material. While the procedures for conducting either uniaxial or triaxial tests to estimate the skeletal deformability characteristics are well known, the exact procedure for estimating the elastic moduli, Poisson's ratio, etc., needs to be better documented so that the interpretations of experimental data can be consistent. The conventional procedure for the pressurization of a saturated sample of the rock and the measurement of the resulting sample strains when the externally applied cell pressure matches the pore fluid pressure is perhaps the best procedure for estimating the compressibility of the solid phases of the porous medium. This, however, is not a routine procedure for low-permeability materials, and substantial pressures need to be applied to ensure that volumetric strains of an accurately measurable value can be recorded.
Also, in such cases the strains could involve irreversible grain boundary frictional slip, and this needs to be excluded from the estimation of the solid material compressibility. Here, we advocate the use of a multi-phasic approach where the theories of composite materials can be used to estimate the compressibility of the solid material composing the porous skeleton. This is a relatively easy approach since XRD evaluations of the mineralogical phase composition are usually carried out to characterize the rock. In relation to the Grimsel granite, the analysis points to a Biot coefficient that has bounds rather than a specific value: i.e. . Values for the Biot coefficient for other types of rocks include the following: westerly granite – α≈0.47; Lac du Bonnet granite in Manitoba, Canada – α=0.73 (Lau and Chandler, 2004); Ruhr sandstone – α≈0.65; Berea sandstone – α≈0.79; Weber sandstone – α≈0.64; Ohio sandstone – α≈0.65; Pecos sandstone – α≈0.83; Boise sandstone – α≈0.85 (further estimates are provided by Zimmerman, 1991); Cobourg limestone – α≈0.66 (see also Table 1 in Detournay and Cheng, 1993). With soft rocks such as chalk, the Biot coefficient is invariably in the range of 0.80 to 1.0 (Alam et al., 2010; Nermoen et al., 2013). For the Callovo-Oxfordian claystone the Biot coefficient is estimated to be in the range of 0.84 (Belmokhtar et al., 2018). Other estimates for a variety of rocks encountered in a coal mining setting are also given by Chen et al. (2019).
The data related to the research are all documented in the article. Additional information can be obtained from the lead author.
The concepts leading to the multi-phasic approach for estimating the Biot coefficient was proposed by APSS. The literature reviews and parameter estimations were performed by APSS, PAS, and MN. The experimental data related to the transversely isotropic modelling of the Grimsel granite were obtained by MN. The calculations of the Voigt–Reuss–Hill and Walpole bounds and their verifications were performed by PAS and APSS. The paper was written by APSS, PAS, and MN and formatted to LaTeX by MN.
The authors declare that they have no conflict of interest.
The work described in the paper was supported by a Discovery Research Grant awarded by the Natural Sciences and Engineering Research Council of Canada. This study is part of the In situ Stimulation and Circulation (ISC) project established by the Swiss Competence Center for Energy Research-Supply of Electricity (SCCER-SoE) with the support of Innosuisse. The third author would like to thank the financial support provided by the Swiss Innovation Agency Innosuisse, which is part of SCCER-SoE. The authors are also grateful to Eduardo Alonso (UPC, Spain), Lyesse Laloui (EPFL, Switzerland), Florian Amman (RWTH, Germany), Martin Mazurek (University of Bern, Switzerland), Stratis Vomvoris (NAGRA, Switzerland), Christian David (Université Cergy-Pontoise, France), Jonny Rutqvist (LBNL, USA), Farid Laouafa (INERIS, France), Son Nguyen (CNSC, Canada), Raphael Schneeberger (NAGRA, Switzerland) and Robert W. Zimmerman (Imperial College, UK) for drawing attention to the literature used in this study and for helpful comments. The authors gratefully acknowledge the comments made by Joseph Doetsch, Institute of Geophysics, Department of Earth Sciences ETH Zurich, which led to improvements in the presentation. The authors, however, are entirely responsible for the statements and conclusions presented in the paper.
This research has been supported by the Natural Sciences and Engineering Research Council of Canada (grant no. RGPIN-2016-04676).
This paper was edited by David Healy and reviewed by two anonymous referees.
Alam, M. M., Borre, M. K., Fabricius, I. L., Hedegaard, K., Røgen, B., Hossain, Z., and Krogsbøll, A. S.: Biot's coefficient as an indicator of strength and porosity reduction: Calcareous sediments from Kerguelen Plateau, J. Petrol. Sci. Eng., 70, 282–297, https://doi.org/10.1016/j.petrol.2009.11.021, 2010. a
Alexandrov, K. S., Rhyzova, T. V., and Beliko, B. P.: The elastic properties of pyroxenes, Sov. Phys. Crystallogr., 8, 589–591, 1964. a
Alonso, E. E. and Alcoverro, J.: DECOVALEX III PROJECT. Modelling of FEBEX In-Situ Test, Task 1 Final Report, Tech. Rep., SKI Report 2005, 202 pp., 2005. a, b, c, d, e
Alonso, E. E., Alcoverro, J., Coste, F., Malinsky, L., Merrien-Soukatchoff, V., Kadiri, I., Nowak, T., Shao, H., Nguyen, T. S., Selvadurai, A. P. S., Armand, G., Sobolik, S. R., Itamura, M., Stone, C. M., Webb, S. W., Rejeb, A., Tijani, M., Maouche, Z., Kobayashi, A., Kurikami, H., Ito, A., Sugita, Y., Chijimatsu, M., Börgesson, L., Hernelind, J., Rutqvist, J., Tsang, C. F., and Jussila, P.: The FEBEX benchmark test: Case definition and comparison of modelling approaches, Int. J. Rock Mech. Min., 42, 611–638, 2005. a, b, c, d, e
Amann, F., Gischig, V., Evans, K., Doetsch, J., Jalali, R., Valley, B., Krietsch, H., Dutler, N., Villiger, L., Brixel, B., Klepikova, M., Kittilä, A., Madonna, C., Wiemer, S., Saar, M. O., Loew, S., Driesner, T., Maurer, H., and Giardini, D.: The seismo-hydromechanical behavior during deep geothermal reservoir stimulations: open questions tackled in a decameter-scale in situ stimulation experiment, Solid Earth, 9, 115–137, https://doi.org/10.5194/se-9-115-2018, 2018. a
Amiguet, J.-L.: Grimsel Test Site, Felskennwerte von intaktem Granit, Zusammenstellung felsmechanischer Laborresultate diverser granitischer Gesteine, Tech. Rep., NAGRA, NIB 85-08, 1985. a, b, c, d, e
Anderson, O. L. and Nafe, J. E.: The bulk modulus-volume relationship for oxide compounds and related geophysical problems, J. Geophys. Res., 70, 3951–3963, https://doi.org/10.1029/sp026p0153, 1965. a
Belmokhtar, M., Delage, P., Ghabezloo, S., and Conil, N.: Drained Triaxial Tests in Low-Permeability Shales: Application to the Callovo-Oxfordian Claystone, Rock Mech. Rock Eng., 51, 1979–1993, https://doi.org/10.1007/s00603-018-1442-0, 2018. a
Biot, M. A.: General theory of three-dimensional consolidation, J. Appl. Phys., 12, 155–164, https://doi.org/10.1063/1.1712886, 1941. a
Bouffier, C.: Stress measurements by overcoring at the Grimsel site. Results from the campaign of August-September 2015 Study Report, Tech. Rep., ETH Zurich, 119 pp., https://doi.org/10.3929/ethz-b-000256660, 2015. a, b, c, d, e, f
Brace, W., Walsh, J., and Frangos, W.: Permeability of Granite under High Pressure, J. Geophys. Res., 73, 2225–2236, 1968. a
Carmichael, R. S. (Ed.): Practical Handbook of Physical Properties of Rocks and Minerals, CRC Press, Boca Raton, FL, 756 pp., 1990. a
Chen, Y., Selvadurai, A. P. S., and Liang, W.: Computational Modelling of Groundwater Inflow During a Longwall Coal Mining Advance: A Case Study from the Shanxi Province, China, Rock Mech. Rock Eng., 52, 917–934, 2019. a
Cheng, A. H. D.: Poroelasticity, Springer-Verlag, Berlin, 877 pp., 2015. a, b
Cohen, L. and Ishai, O.: The elastic properties of three-phase composites, J. Compos. Mater., 1, 390–403, 1967. a
Dambly, M., Nejati, M., Vogler, D., and Saar, M. O.: On the direct measurement of the shear moduli in transversely isotropic rocks using the uniaxial compression test, Int. J. Rock Mech. Min., 113, 220–240, 2019. a, b, c, d, e
David, C., Wassermann, J., Amann, F., Klaver, J., Davy, C., Sarout, J., Esteban, L., Rutter, E. H., Hu, Q., Louis, L., Delage, P., Lockner, D. A., Selvadurai, A. P. S., Vanorio, T., Hildenbrand, A. A., Meredith, P. G., Browning, J., Mitchell, T. M., Madonna, C., Billiotte, J., Reuschlé, T., Lasseux, D., Fortin, J., Lenormand, R., Loggia, D., Nono, F., Boitnott, G., Jahns, E., Fleury, M., Berthe, G., Braun, P., Grégoire, D., Perrier, L., Polito, P., Jannot, Y., Sommier, A., Krooss, B., Fink, R., and Clark, A.: KG2B, a collaborative benchmarking exercise for estimating the permeability of the Grimsel granodiorite – Part 2: Modelling, microstructures and complementary data, Geophys. J. Int., 215, 825–843, https://doi.org/10.1093/GJI/GGY305, 2018a. a
David, C., Wassermann, J., Amann, F., Lockner, D. A., Rutter, E. H., Vanorio, T., Hildenbrand, A. A., Billiotte, J., Reuschlé, T., Lasseux, D., Fortin, J., Lenormand, R., Selvadurai, A. P. S., Meredith, P. G., Browning, J., Mitchell, T. M., Loggia, D., Nono, F., Sarout, J., Esteban, L., Davy, C., Louis, L., Boitnott, G., Madonna, C., Jahns, E., Fleury, M., Berthe, G., Delage, P., Braun, P., Grégoire, D., Perrier, L., Polito, P., Jannot, Y., Sommier, A., Krooss, B., Fink, R., Hu, Q., Klaver, J., and Clark, A.: KG2B, a collaborative benchmarking exercise for estimating the permeability of the Grimsel granodiorite – Part 1: Measurements, pressure dependence and pore-fluid effects, Geophys. J. Int., 215, 799–824, https://doi.org/10.1093/GJI/GGY304, 2018b. a
Davis, R. O. and Selvadurai, A. P. S.: Elasticity and Geomechanics, Cambridge University Press, Cambridge, 198 pp., 1996. a
Detournay, E. and Cheng, A. H. D.: Comprehensive rock engineering: Principles, practice and projects, in: Hudson JA, ed., Fundamentals of Poroelasticity, Vol. 1., Pergamon Press, Oxford, 113–171, 1993. a, b
Doetsch, J., Gischig, V., Villiger, L., Krietsch, H., Nejati, M., Amann, F., Jalali, M., Madonna, C., Maurer, H., Wiemer, S., Driesner, T., and Giardini, D.: Subsurface fluid pressure and rock deformation monitoring using seismic velocity observations, Geophys. Res. Lett., 45, https://doi.org/10.1029/2018GL079009, 2018. a
Dupray, F., François, B., and Laloui, L.: Analysis of the FEBEX multi-barrier system including thermoplasticity of unsaturated bentonite, Int. J. Numer. Anal. Meth. Geomech., 37, 399–422, 2013. a
Dutler, N., Nejati, M., Valley, B., Amann, F., and Molinari, G.: On the link between fracture toughness, tensile strength, and fracture process zone in anisotropic rocks, Eng. Fract. Mech., 201, 56–79, 2018. a
Francfort, G. A. and Murat, F.: Homogenization and optimal bounds in linear elasticity, Arch. Ration. Mech. An., 94, 307–334, https://doi.org/10.1007/BF00280908, 1986. a
Garralón, A., Gómez, P., Turrero, M. J., Torres, E., Buil, B., and Peña, J.: Hydrogeochemical characterization of the groundwater in the FEBEX gallery, National Cooperative for the Disposal of Radioactive Waste, Tech. Rep., NAGRA Arbeitsbericht, NAB 16-14, Wettingen, Switzerland, 125 pp., 2017. a
Gens, A., Garcia-Molina, A. J., Olivella, S., Alonso, E. E., and Huertas, F.: Analysis of a full scale in situ testing simulating repository conditions, Int. J. Numer. Anal. Met., 22, 515–548, https://doi.org/10.1002/(SICI)1096-9853(199807)22:7<515::AID-NAG926>3.0.CO;2-8, 1998. a
Gischig, V. S., Doetsch, J., Maurer, H., Krietsch, H., Amann, F., Evans, K. F., Nejati, M., Jalali, M., Valley, B., Obermann, A. C., Wiemer, S., and Giardini, D.: On the link between stress field and small-scale hydraulic fracture growth in anisotropic rock derived from microseismicity, Solid Earth, 9, 39–61, https://doi.org/10.5194/se-9-39-2018, 2018. a
Goncalves, P., Oliot, E., Marquer, D., and Connolly, J. A.: Role of chemical processes on shear zone formation: An example from the grimsel metagranodiorite (Aar massif, Central Alps), J. Metamorph. Geol., 30, 703–722, https://doi.org/10.1111/j.1525-1314.2012.00991.x, 2012. a
Hashin, Z. and Shtrikman, S.: A variational approach to the theory of the elastic behaviour of multiphase materials, J. Mech. Phys. Solids, 11, 127–140, 1963. a
Hearmon, R. F. S.: An Introduction to Applied Anisotropic Elasticity, Clarendon Press, Oxford, 136 pp., 1961. a
Hill, R.: The elastic behaviour of a crystalline aggregate, Proceedings of the Physical Society A, 65, 349–354, 1952. a, b
Hill, R.: A self-consistent mechanics of composite materials, J. Mech. Phys. Solids, 13, 213–222, 1965. a, b
Jalali, M., Gischig, V., Doetsch, J., Naf, R., Krietsch, H., Klepikova, M., Amann, F., and Giardini, D.: Transmissivity changes and microseismicity induced by small-scale hydraulic fracturing tests in crystalline rock, Geophys. Res. Lett., 45, 2265–2273, 2018. a
Jokelainen, L., Meski, T., Lindberg, A., Soler, J. M., Siitari-Kauppi, M., Martin, A., and Eikenberg, J.: The determination of 134Cs and 22Na diffusion profiles in granodiorite using gamma spectroscopy, J. Radioan. Nucl. Ch. Ar., 295, 2153–2161, https://doi.org/10.1007/s10967-012-2268-y, 2013. a, b
Ju, J. W. and Chen, T. M.: Effective elastic moduli of two-phase composites containing randomly dispersed spherical inhomogeneities, Acta Mech., 103, 123–144, https://doi.org/10.1007/BF01180222, 1994a. a
Ju, J. W. and Chen, T. M.: Micromechanics and effective moduli of elastic composites containing randomly dispersed ellipsoidal inhomogeneities, Acta Mech., 103, 103–121, https://doi.org/10.1007/BF01180221, 1994b. a
Kant, M. A., Ammann, J., Rossi, E., Madonna, C., Höser, D., and Rudolf von Rohr, P.: Thermal properties of Central Aare granite for temperatures up to 500 ∘C: Irreversible changes due to thermal crack formation, Geophys. Res. Lett., 44, 771–776, https://doi.org/10.1002/2016GL070990, 2017. a
Keusen, H., Ganguin, J., Schuler, P., and Buletti, M.: Technical report 87-14 E: Grimsel test site geology, Tech. Rep., GEOTEST: Zollikofen/Bern, 169 pp., 1989. a, b, c, d, e, f, g, h, i
Krietsch, H., Gischig, V., Evans, K., Doetsch, J., Dutler, N. O., Valley, B., and Amann, F.: Stress Measurements for an In Situ Stimulation Experiment in Crystalline Rock: Integration of Induced Seismicity, Stress Relief and Hydraulic Methods, Rock Mech. Rock Eng., 52, 517–542, 2019. a, b, c, d, e, f, g
Lau, J. S. O. and Chandler, N. A.: Innovative laboratory testing, Int. J. Rock Mech. Min., 41, 1427–1445, 2004. a
Lekhnitskii, S. G.: Theory of Elasticity of an Anisotropic Elastic Body, Holden-Day, San Francisco, 404 pp., 1963. a
Lin, C. C.: Elasticity of calcite: Thermal evolution, Phys. Chem. Miner., 40, 157–166, https://doi.org/10.1007/s00269-012-0555-3, 2013. a
Lin, P. J. and Ju, J. W.: Effective elastic moduli of three-phase composites with randomly located and interacting spherical particles of distinct properties, Acta Mech., 208, 11–26, https://doi.org/10.1007/s00707-008-0114-7, 2009. a
Mavko, G. M., Dvorkin, J., and Mukerji, T.: The Rock Physics Handbook, Tools for seismic analysis of porous media, Cambridge University Press, Cambridge, 571 pp., 2009. a
Missana, T. and Garcia-Gutiérrez, M.: Comparison of the Cesium adsorption on different crystalline rocks, in 1st Workshop Proceedings of the Collaborative Project “Crystalline Rock Retention Processses”, (7th EC FP CP CROCK), edited by: Rabung, T., Molinero, J., Garcia, D., and Montoya, V., KIT Scientific Publishing, Barcelona, Spain, 121–130, 2012. a, b
Moos, D., Dvorkin, J., and Hooks, A. J.: Application of theoretically derived rock physics relationships, Los Angeles “Critical porosity”, Geophys. Res. Lett., 24, 329–332, 1997. a
Möri, A., Mazurek, M., Adler, M., Schild, M., Siegesmund, S., Vollbrecht, A., Ota, K., Ando, T., Alexander, R., Smith, P. A., Haag, P., and Buehler, Ch.: The Nagra-JNC in situ study of safety relevanr radionuclide retardation in fractured crystalline rock, IV: The in situ study of matrix porosity in the vicinity of a water conducting fracture, Tech. Rep., NAGRA Technical Report, 00-08, Baden, Switzerland, 115 pp., 2003. a
Moulu, J. C., Kalaydjian, F., Tsakiroglou, C. D., Burganos, V. N., Payatakes, A. C., Yao, J., Thovert, J.-F., and Adler, P.-M.: Characterization, reconstruction and transport properties of the Vosges sandstone, Revue de L'Institut Francais du Petrole, 52, 3–21, 1997. a
Nejati, M.: On the anisotropy of mechanical properties in Grimsel granodiorite, Tech. Rep., ETH Zurich, https://doi.org/10.3929/ethz-b-000289969, 2018. a, b, c, d, e, f
Nejati, M., Dambly, M., and Saar, M. O.: A methodology to determine the elastic properties of anisotropic rocks from a single uniaxial compression test, J. Rock Mech. Geotech. Eng., https://doi.org/10.1016/j.jrmge.2019.04.004, 2019. a, b, c, d, e, f, g
Nermoen, A., Korsnes, R., Christensen, H. F., Trads, N., Hiorth, A., and Madland, M. V.: Measuring the Biot stress coefficient and its implications on the effective stress estimate, Proc. 47th US Rock Mech./Geomech. Symposium, San Francisco, CA, USA, ARMA, p. 282, 2013. a
Nguyen, T. S., Selvadurai, A. P. S., and Armand, G.: Modelling the FEBEX THM experiment using a state surface approach, Int. J. Rock Mech. Min., 42, 639–651, https://doi.org/10.1016/j.ijrmms.2005.03.005, 2005. a
Pahl, A., Heusermann, S., Bräuer, V., and Glöggler, W.: Grimsel Test Site. Rock Stress Investigations, Tech. Rep., NAGRA Technical Report, 88-39E, Baden, Switzerland, 151 pp., 1989. a, b, c, d, e, f
Rabung, T., Molinero, J., Garcia, D., and Montoya, V.: 1st Workshop Proceedings of the Collaborative Project “Crystalline Rock Retention Processses”, (7th EC FP CP CROCK), KIT Scientific Publishing, Barcelona, Spain, 206 pp., 2012. a
Redfern, S. A. and Angel, R. J.: High-pressure behaviour and equation of state of calcite, CaCO3, Contrib. Mineral. Petr., 134, 102–106, https://doi.org/10.1007/s004100050471, 1999. a
Reuss, A.: Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle, J. Appl. Math. Mech., 9, 49–58, 1929. a, b
Rutqvist, J., Rejeb, A., M., T., and Tsang, C.-F.: Analyses of coupled hydrological-mechanical effects during drilling of the FEBEX tunnel at Grimsel, in: Proceedings of GeoProc 2003, edited by: Stephansson, O., Hudson, J. A., and Jing, L., Stockholm, 196, 13–15 October 2003, 44, 114–119, 2003. a
Schaltegger, U.: The Central Aar Granite: highly differentiated calc-alkaline magmatism in the Aar Massif (Central Alps, Switzerland), Eur. J. Mineral., 2, 254–259, 1990a. a
Schaltegger, U.: Post-magmatic resetting of Rb-Sr whole rock ages – a study in the Central Aar Granite (Central Alps, Switzerland), Geol. Rundsch., 79, 709–724, 1990b. a
Schaltegger, U. and Corfu, F.: The age and source of late Hercynian magmatization in the central Alps: evidence from precise U-Pb ages and initial Hf isotopes, Contrib. Mineral. Petr., 111, 329–344, 1992. a
Schaltegger, U. and Krähenbühl, U.: Heavy rare earth element enrichment in granites of the Aar Massif (Central Alps, Switzerland), Chem. Geol., 89, 49–63, 1990. a, b
Schild, M., Siegesmund, S., Vollbrecht, A., and Mazurek, M.: Characterization of granite matrix porosity and pore-space geometry by in situ and laboratory methods, Geophys. J. Int., 146, 111–125, 2001. a
Schilling, F. R., Sinogeikin, S. V., Hauser, M., and Bass, J. D.: Elastic properties of model basaltic melt compositions at high temperatures, J. Geophys. Res.-Solid Ea., 108, 2304, https://doi.org/10.1029/2001jb000517, 2003. a
Selvadurai, A. P. S.: Mechanics of Poroelastic Media, Kluwer Academic Publishers, the Netherlands, 394 pp., 1996. a
Selvadurai, A. P. S.: Partial Differential Equations in Mechanics, Vol. 2, The Bi-harmonic Equation, Poisson's equation, Springer-Verlag, Berlin, 698 pp., 2000. a
Selvadurai, A. P. S.: Stationary damage modelling of poroelastic contact, Int. J. Solids Struct., 41, 2043–2064, https://doi.org/10.1016/j.ijsolstr.2003.08.023, 2004. a
Selvadurai, A. P. S.: The Analytical Method in Geomechanics, Appl. Mechan. Rev., 60, 87–106, https://doi.org/10.1115/1.2730845, 2007. a
Selvadurai, A. P. S.: Influence of residual hydraulic gradients on decay curves for one-dimensional hydraulic pulse tests, Geophys. J. Int., 177, 1357–1365, https://doi.org/10.1111/j.1365-246X.2008.04047.x, 2009. a
Selvadurai, A. P. S.: The Biot coefficient for a low permeability heterogeneous limestone, Continuum Mech. Therm., 31, 939–953, https://doi.org/10.1007/s00161-018-0653-7, 2019. a
Selvadurai, A. P. S. and Carnaffan, P.: A transient pressure pulse method for the mesurement of permeability of a cement grout, Can. J. Civil Eng., 24, 489–502, https://doi.org/10.1139/l96-132, 1997. a
Selvadurai, A. P. S. and Glowacki, A.: Evolution of permeability hysteresis of Indiana Limestone during isotropic compression, Ground Water, 46, 113–119, 2008. a
Selvadurai, A. P. S. and Głowacki, A.: Stress-Induced Permeability Alterations in an Argillaceous Limestone, Rock Mech. Rock Eng., 50, 1079–1096, https://doi.org/10.1007/s00603-016-1153-3, 2017. a
Selvadurai, A. P. S. and Głowacki, A.: Estimates for the local permeability of the Cobourg limestone, J. Rock Mech. Geotech. Eng., 10, 1009–1019, 2018. a
Selvadurai, A. P. S. and Najari, M.: Laboratory-scale hydraulic pulse testing: influence of air fraction in cavity on estimation of permeability, Géotechnique, 65, 126–134, https://doi.org/10.1680/geot.14.p.174, 2015. a
Selvadurai, A. P. S. and Selvadurai, P. A.: Surface permeability tests: Experiments and modelling for estimating effective permeability, P. Roy. Soc. A, 466, 2819–2846, https://doi.org/10.1098/rspa.2009.0475, 2010. a
Selvadurai, P. A. and Selvadurai, A. P. S.: On the effective permeability of a heterogeneous porous medium: The role of the geometric mean, Philos. Mag., 94, 2318–2338, 2014. a, b
Selvadurai, A. P. S. and Shirazi, A.: Mandel-Cryer effects in fluid inclusions in damage-susceptible poroelastic geologic media, Comput. Geotech., 31, 285–300, https://doi.org/10.1016/j.compgeo.2004.02.008, 2004. a
Selvadurai, A. P. S. and Shirazi, A.: An elliptical disc anchor in a damage-susceptible poroelastic medium, Int. J. Num. Meth. Eng., 63, 2017–2039, https://doi.org/10.1002/nme.1354, 2005. a
Selvadurai, A. P. S. and Suvorov, A. P.: Boundary heating of poro-elastic and poro-elasto-plastic spheres, P. Roy. Soc. A, 468, 2779–2806, 2012. a
Selvadurai, A. P. S. and Suvorov, A. P.: Thermo-poromechanics of afluid-filledcavityina fluid-saturated geomaterial, P. Roy. Soc. A, 470, 20130634, https://doi.org/10.1098/rspa.2013.0634, 2014. a
Selvadurai, A. P. S. and Suvorov, A. P.: Thermo-poroelasticity and Geomechanics, Cambridge University Press, Cambridge, 250 pp., 2016. a
Selvadurai, A. P. S., Letendre, A., and Hekimi, B.: Axial flow hydraulic pulse testing of an argillaceous limestone, Environ. Earth Sci., 64, 2047–2058, https://doi.org/10.1007/s12665-011-1027-7, 2011. a, b
Selvadurai, A. P. S., Suvorov, A. P., and Selvadurai, P. A.: Thermo-hydro-mechanical processes in fractured rock formations during a glacial advance, Geosci. Model Dev., 8, 2167–2185, https://doi.org/10.5194/gmd-8-2167-2015, 2015. a, b
Sisodia, P. and Verma, M. P.: Polycrystalline elastic moduli of some hexagonal and tetragonal materials, Phys. Status Solidi, 122, 525–534, 1990. a
Stalder, H. A.: Petrographische und mineralogiche Untersuchungen im Grimselgebeit, Schweiz. Miner. Petrog., 44, 187–398, 1964. a
Steck, A. and Burri, G.: Chemismus und paragenesen von granaten aud granitgneisen der Grünschiefer – und amphibolitfazies der Zentralapen, Schweiz. Miner. Petrog., 51, 534–538, 1971. a
Talbot, D. R., Willis, J. R., and Nesi, V.: On improving the hashin-shtrikman bounds for the effective properties of three-phase composite media, IMA J. Appl. Math., 54, 97–107, https://doi.org/10.1093/imamat/54.1.97, 1995. a
Terzaghi, K.: Die Berechnung der Durchlassigkeitsziffer des Tones aus Dem Verlauf der Hydrodynamischen Spannungserscheinungen, Akad. Wissensch., Wien Sitzungsber Mathnaturwissensch Klasse IIa, 142, 125–138, 1923. a
Ting, T. C. T.: Anisotropic Elasticity: Theory and Applications, Oxford University Press, Oxford, 570 pp., 1996. a
Verruijt, A.: Theory and Problems of Poroelasticity, Delft University of Technology, the Netherlands, 266 pp., 2015. a
Voigt, W.: Lehrbuch der Kristallphysik, edited by: Teubner, B. G., Leipzig, 35, 1928. a, b
Walpole, L.: On bounds for the overall elastic moduli of inhomogeneous systems – I, J. Mech. Phys. Solids, 14, 151–162, 1966. a
Wang, H. F.: Theory of Linear Poroelasticity with Applications to Geomechanics and Hydrogeology, Princeton University Press, Princeton, 287 pp., 2000. a, b
Wenning, Q. C., Madonna, C., de Haller, A., and Burg, J.-P.: Permeability and seismic velocity anisotropy across a ductile-brittle fault zone in crystalline rock, Solid Earth, 9, 683–698, https://doi.org/10.5194/se-9-683-2018, 2018. a, b, c, d
Wüthrich, H.: Rb-Sr-Altcrsbestimmungen am alpin überprägten Aarmassiv, Schweiz. Miner. Petrogr., 45, 876–971, 1965. a
Yue, Z. Q. and Selvadurai, A. P. S.: On the mechanics of a rigid disc inclusion embedded in a fluid saturated poroelastic medium, Int. J. Eng. Sci., 33, 1633–1662, 1995. a
Zhu, W., Hughes, J. J., Bicanic, N., and Pearce, C. J.: Nanoindentation mapping of mechanical properties of cement paste and natural rocks, Mater. Charact., 58, 1189–1198, 2007. a
Ziegler, M. and Amann, F.: Laboratory test results obtained from core samples from the Grimsel III borehole at Kessiturm, Tech. Rep., Internal Report, Ingenieurgeologie, ETH Zurich, 10 pp., 2012. a, b, c, d, e
Zimmerman, R. W.: Compressibility of Sandstones, Developments in Petroleum Science, Elsevier, Amsterdam, 1991. a