the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Uniaxial compression of calcite single crystals at room temperature: insights into twinning activation and development
Camille Parlangeau
Alexandre Dimanov
Olivier Lacombe
Simon Hallais
Jean-Marc Daniel
E-twinning is a common plastic deformation mechanism in calcite deformed at low temperature. Strain rate, temperature and confining pressure have negligible effects on twinning activation which is mainly dependent on differential stress. The critical resolved shear stress (CRSS) required for twinning activation is dependent on grain size and strain hardening. This CRSS value may obey the Hall–Petch relation, but due to sparse experimental data its actual evolution with grain size and strain still remains a matter of debate.
In order to provide additional constraints on twinning activation and development, new mechanical tests were carried out at room temperature on unconfined single crystals of calcite, with different sizes and crystallographic orientations. Uniaxial deformation was performed at a controlled displacement rate, while the sample surface was monitored using optical microscopy and a high-resolution CCD (charge-coupled device) camera. The retrieved macroscopic stress–strain behavior of the crystals was correlated with the surface observations of the deformation process.
Results show (1) the onset of crystal plasticity with the activation of the first isolated mechanical twins during the strain hardening stage, and (2) the densification and thickening of twin lamellae during the steady-state flow stress stage. Such thickening of twin lamellae at room temperature emphasizes that calcite twin morphology is not controlled solely by temperature. The different values for the CRSS obtained for the activation of isolated twins and for the onset of twin densification and thickening raises questions regarding the appropriate value to be considered when using calcite twin data for stress inversion purposes.
- Article
(3983 KB) - Full-text XML
-
Supplement
(502 KB) - BibTeX
- EndNote
Calcite is a common mineral in the Earth's upper crust, forming different types of sedimentary (carbonates) or metamorphic (marbles) rocks. Deformation modes of calcite aggregates have been investigated experimentally since the early 1950s (e.g., Turner, 1949; Griggs and Miller, 1951; Handin and Griggs, 1951; Turner and Ch'ih, 1951; Griggs et al., 1951, 1953; Friedman and Heard, 1974; Schmid and Paterson, 1977; Rowe and Rutter, 1990; Lacombe and Laurent, 1996; De Bresser and Spiers, 1993, 1997; Laurent et al., 2000; Rybacki et al., 2013). These studies have provided information about different mechanisms allow calcite crystals to accommodate deformation under various pressure (P), temperature (T) and strain rate conditions. E-twinning is the plastic deformation mechanism that prevails in calcite crystals at low strain and low temperature. Strain rate, temperature and isotropic stress state (confining pressure) have negligible effects on twinning activation which is mainly dependent on differential stress and grain size (Rowe and Rutter, 1990). Temperature has an impact on the thickness of twin lamellae (Burkhard, 1993). Twin lamellae are commonly observed to be thin (≤1 µm) below 170–200 ∘C and to become thicker (2–5 µm) above this temperature for a given amount of twinning strain (e.g., Ferrill et al., 2004). However, this relationship between twin thickness and temperature has recently been challenged by Rybacki et al. (2013) who emphasized that the increasing duration of stress application – hence the increasing strain – may cause widening of twin lamellae even at room temperature. Another matter of debate deals with the existence (and with the value) of a threshold stress for the activation of twinning, which is defined (as for crystal slip plasticity) as a critical resolved shear stress value (CRSS) (Tullis, 1980; Ferrill, 1998). Several authors have tried to constrain this value (Turner et al., 1954; Lacombe and Laurent, 1996; De Bresser and Spiers, 1997; Laurent et al., 2000; Lacombe, 2001; Rocher et al., 2004; Covey-Crump et al., 2017). The CRSS is mainly dependent on grain size and is subjected to strain hardening: its value increases with the amount of accommodated strain and decreases with increasing grain size (Turner et al., 1954; Tullis, 1980; Rowe and Rutter, 1990; Laurent et al., 2000). Therefore, this CRSS value may obey the Hall–Petch relation, but due to sparse experimental data, the actual evolution of the CRSS with grain size and strain still remains poorly constrained.
In summary, most mechanical experiments to date have been carried out at high temperature in order to investigate gliding systems in calcite. Very few data are available on the plastic behavior of calcite crystals at low temperature, despite the ubiquitous deformed carbonate rocks in sedimentary basins. Hence, new mechanical tests were carried out at room temperature on unconfined single crystals of calcite, which were different sizes and had different crystallographic orientations. Uniaxial deformation was performed at a controlled displacement rate, while the sample surface was monitored using optical microscopy (reflected light) and a high-resolution CCD (charge-coupled device) camera. The retrieved macroscopic stress–strain behavior of the crystals was correlated with the surface observations of the deformation process. Special attention was paid to the resolved shear stress value required to activate twinning and to the sequence of activation and thickening of calcite twins.
2.1 Materials
In addition to the grain-size dependence of twinning, Newman (1994) highlighted the fact that the grain-size distribution could have an impact on the CRSS value. This author indicated that a grain surrounded by 10 grains is more easily twinned than the same grain surrounded by only 5 grains. Thus, in order to circumvent this problem, we decided to work on single crystals.
Icelandic spars were first deformed in order to establish the appropriate deformation protocol to be applied in terms of sample preparation, loading rates and conditions for the in situ optical/SEM monitoring (Supplement). This preparation phase allowed, for instance, to select the most suitable CCD cameras and to establish the SEM imaging conditions. However, because the spars utilized always contained preexisting cleavage cracks, twin lamellae and micro-fluid inclusions, they could not be used further (1) to produce several perfectly similar samples with respect to size, crystal orientation, and preexisting defects, or (2) to accurately infer the CRSS value of interest because the grain-scale heterogeneities may have caused stress concentrations and because the initial strain was associated with some amount of work-hardening that could not be precisely quantified. A way to remove this work-hardening effect would have been to heat the samples. De Bresser and Spiers (1997) healed the initial intracrystalline strain by annealing at a temperature of 500 ∘C for 24 h: healing occurs via the formation of subgrains as a result of progressively stacking of free dislocations at subgrain boundaries. However, these subgrain boundaries could have affected the propagation and spreading of twins and caused non-uniform stress distribution at the grain scale, thus biasing the results.
The choice was then made to perform uniaxial compression of single crystals of pure synthetic calcite (CaCO3) of optical quality (purchased from SurfaceNet). Working on such synthetic material ensured the initial quality of the deformed single crystals: limited dislocation density, and crystals free from fluid inclusions, cleavages and twins. In order to assess the grain-size effect, we tested parallelepiped shaped specimens with dimensions of and mm3. Two samples had their long axis along the direction and two samples along the direction (Fig. 1), meaning that the uniaxial stress could be applied along two different crystallographic orientations.
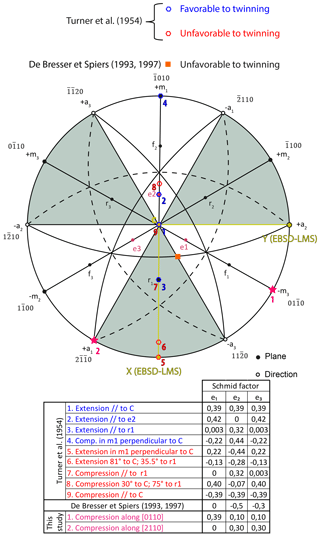
Figure 1Calcite lattice projection in Schmid's lower hemisphere with information regarding the force vector applied in previous studies (Turner et al., 1954; De Bresser and Spiers, 1993, 1997) and in this study. The table summarizes the Schmid factor calculated for each e-twin plane (e1, e2 and e3) as a function of the applied force orientation. Pink stars correspond to the applied compression orientations used on the synthetic single-crystal of calcite.
2.2 Methods
In the previous studies calcite samples were always observed in post mortem conditions. As the purpose of this study was to detect the very early activation of twinning and to characterize its subsequent development, the choice was made to continuously monitor the experiments using either optical microscopy (with a high-resolution camera and SYLVIA software, Bornert et al., 2010) or during in situ SEM testing under low vacuum (60–80 Pa) conditions with a miniaturized uniaxial press. Macroscopic deformation was provided by an optical displacement sensor (Solartron), which measures the displacement of the mobile piston. This is the first time that the characterization of the twinning deformation of calcite has been performed coupled with in situ microscopy.
All experiments were performed at the constant strain rate of 10−5 s−1, and at room temperature. The compression was applied along the longest axis of the crystals and the corresponding Schmid factors were calculated for the two differently oriented kinds of single crystals (Fig. 1). When the first twin lamellae appeared, the sample was unloaded and removed from the press. EBSD (electron backscattering diffraction, FEI Quanta 600, AZtecHKL) analysis was performed in order to determine whether the expected e-twins (with the highest Schmid factor) had been activated. Following this, the single crystal was replaced into the deformation rig and further subjected to uniaxial compression in order to observe the evolution of twinning deformation (twin growth, densification and widening) and the corresponding strain hardening with the increase of the applied axial strain.
3.1 Results
Three representative experimental results are shown in the following. In general, the loading curves present three distinct major stages. Stage I (or phase-in) corresponds to the emplacement of the loading column, which refers to the alignment of pistons and samples (and possibly edge effects of the loaded faces, due to small departures from parallelism). Stage II represents the pseudo-elastic regime, which averages the sample behavior and the compliance of the machine. Hence, it is characterized by an apparent Young modulus, which is substantially lower than expected for calcite (≈ 1.3 GPa). Stage III exhibits dominantly the plastic regime, with twinning, but also a minor contribution from micro-cracking. Stage III may be divided in two substages. Stage IIIa lasts about 1–1.5 % shortening and is characterized by pronounced strain hardening, with the activation of a few early twins. Stage IIIb lasts 2–4 % shortening, corresponding to a continuous densification of twinning. The latter stage is characterized by a strongly serrated loading curve. The serrations fluctuate around a nearly steady-state flow stress, establishing very limited strain hardening, or a “plateau-like” regime.
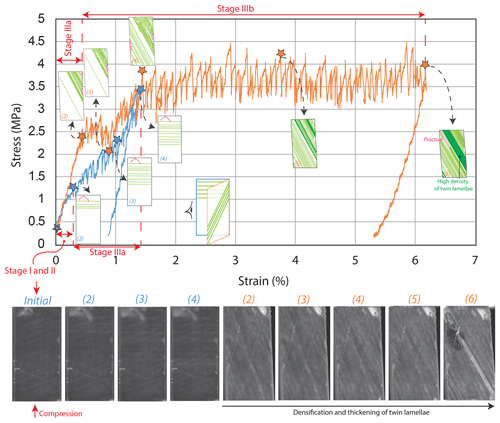
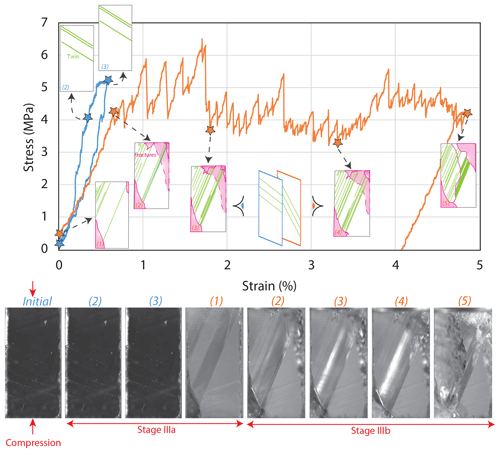
Figure 2Results from the mm3 sample compressed along the direction. Stress (MPa) vs. strain (%) curve showing the three stages described in the text. Between the blue and orange curves, the sample was removed from the press in order to determine the orientation of the first twin lamella. Each star on the curves corresponds to one of the high-resolution pictures below. In the different pictures, the twin lamellae are represented in light green, and a high density of twin lamellae is highlighted using dark green. Fractures are displayed in pink.
Figure 2 shows the loading curve of the first experiment carried out on a small sample ( mm3), compressed along (configuration 1 of this study, Fig. 1). The specimen was first deformed until 1.4 % shortening in stage IIIa. The very first twins were detected at about 0.3 % shortening. Twin activity progressively increased during strain hardening, which is indicated by the numerous drops in axial stress (serrations). After reaching 1.4 % shortening the specimen was completely unloaded and removed for observations, before a second compression test was carried out. At this step the prescribed shortening was of about 151 µm. High-resolution SEM micrographs were used to measure twin lamellae thickness, which allowed us to determine that twinning contributed to this axial displacement by a length of 116 µm. Optically we could see, by transparency, a few twin lamellae that did not cross the whole crystal up to the surface which could explain part of the difference between estimated shortening by twinning and the prescribed shortening. The optical error of the measurement of the thickness of individual twin lamella on pictures may have also contributed to the mismatch. During the second loading, the sample rapidly reached stage IIIb, characterized by nearly steady-state flow stress. This plateau-like curve is serrated, and composed of numerous and regular segments, corresponding to strain hardening stages followed by sudden stress drops. The optical monitoring shows that the latter can be associated with the continuous densification of twinning. The test was stopped at the onset of micro-cracking prior to failure at about 6 % shortening (Fig. 2).
The thickness of the first twin lamellae was about 2–7 µm. At the very beginning of loading, micro-cracking nucleated right at the upper interface between the piston and the single crystal (Fig. 2). The lack of confining pressure probably favored micro-fracturing. However, (1) the micro-crack was localized very close to the interface, and (2) it did not propagate further within the bulk sample during loading. These observations indicate that micro-cracking did not interfere with the overall response of the sample, which remained dominated by twinning plasticity. The second loading phase of the sample led to the establishment of stage IIIb (Fig. 2), which showed a strong change in the rate of twinning activation, with a period of high densification and also of twin lamellae thickening. These events are clearly correlated with the different strain hardening stages and sudden stress drops observed on the serrated loading curve representing the macroscopic behavior. Overall thickening of twin lamellae occurred in three steps: (1) densification of twin lamellae, (2) individual thickening of each existing twin lamella and (3) merging of thickened neighboring twin lamellae. For the millimeter-sized single crystals compressed up to a few percent at room temperature and pressure, the thickness of a twin lamella can reach 90 µm for the largest crystals. During stage IIIa, the sample was removed from the uniaxial press to determine the twin lamellae crystallographic orientation using EBSD. This orientation was mostly used to calculate the Schmid factor and the associated applied resolved shear stress – particularly the value at twin activation (CRSS). The results show that for all of the samples the expected (Fig. 1) twin lamellae were activated during the experiments. For the present orientation, with loading along , the calculated Schmid factor is 0.39 and the corresponding CRSS is 0.44 MPa.
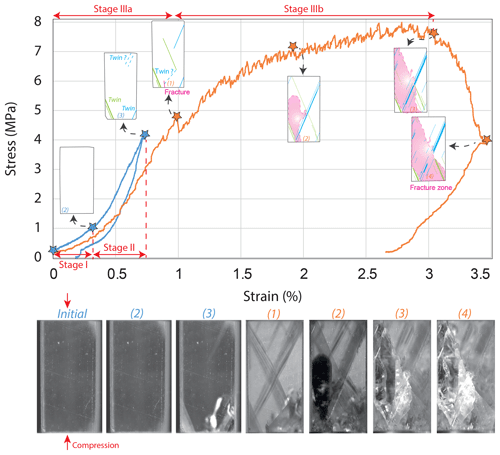
The second experiment was carried out on single crystals of both sizes ( and mm3) compressed along (Fig. 1). For the smaller sample, the macroscopic behavior is comparable to that previously described, with three different stages: (I) emplacement; (II) elastic deformation; (IIIa) plastic yielding and strain hardening flow (blue curve, Fig. 3); and (IIIb) macroscopically steady-state plastic flow, characterized by a serrated plateau-like stress–strain curve. However, the latter is less regular than the stage IIIb curve in the Fig. 3. The optical monitoring allowed similar observations as for the previous sample (Fig. 2), aside from the fact that there was no early micro-cracking during stage IIIa (Fig. 3). The densification of twins during stage IIIb was not as intense as in the previous experiment (Fig. 3). For this sample orientation, the activation of two equivalent twin systems (i.e., with the same Schmid factor, Fig. 1) was expected. However, only one system was activated, possibly due to a small disorientation of the crystal lattice of less than 3∘. The CRSS calculated using the Schmid factor at the appearance of the twinned lamella was 1.25 MPa.
The last experiment was carried out on a larger sample ( mm3), but with the same orientation as the previous experiment ( configuration 2 of this study, Fig. 1). The macroscopic behavior is roughly similar to the previous experiment, with emplacement, pseudo-elastic and strain hardening stages (Fig. 4). However, it also differs with respect to some details. The plastic yielding is more difficult to determine. The gradual slope change observed at about 0.3 %–0.4 % of axial deformation represents the transition from emplacement to pseudo-elasticity, without any activation of twinning. The very first twins appeared at about 0.7 % of axial deformation and at 4 MPa flow stress. These observations are roughly in agreement with those from the previous test, where twinning appeared at about 0.5 % and 4 MPa sample shortening and strength. But, as opposed to the previous case, we observed the activation of the two distinct (but equivalent) twin systems, whereas in the previous experiment only one system was active, despite the fact that both samples have the same crystallographic orientation with respect to the uniaxial loading (configuration 2 of this study, Fig. 1). Another major difference in the macroscopic behavior is that stage IIIb does not present a plateau-like stress–strain curve. The stress–strain curve is serrated, but as a whole it shows a strain hardening evolution, until extensive micro-cracking develops at about 8 MPa flow stress and leads to sample failure. Optical monitoring and EBSD characterization show the development of the twinning patterns (the two systems are represented in blue and green, Fig. 4) during the different stages. Stage IIIa shows the first twins and limited micro-cracking. Stage IIIb shows the densification and the thickening of both twin systems, in addition to micro-cracking. Observed strain hardening is probably due to the interactions between the two simultaneously active twin systems. The densification and twin lamellae thickening are not as pronounced as in the previous test. The CRSS calculated using the Schmid factor at the appearance of twinned lamella is 1.24 MPa for both twinned planes.
3.2 Discussion
Despite the rather limited number of deformed synthetic crystals (four), our results show qualitatively the same patterns for the loading curves as for the Icelandic spars (Supplement), which makes us confident about the reproducibility of the results and the conclusions drawn regarding the effect of orientation and grain size.
3.2.1 Macroscopic behavior of deformed samples
The macroscopic deformation behavior of all of our single crystals exhibits three major stages revealed by the stress–strain curves, which is in agreement with the findings of de Bresser and Spiers (1993, 1997). The initial stage (I) is the period of preloading during which full contact between pistons and samples is progressively established; this is not the same for each specimen, as it depends on the exact sample geometry (parallelism of loaded faces). Eventual stress concentrations would expectedly be more pronounced during this emplacement stage; however, the micro-cracks did not appear at this stage. Micro-cracks essentially developed later on, during the pseudo-elastic phase (stage II) and the plastic phase (stage III). This may indicate that micro-cracking is a complementary and necessary deformation mechanism, allowing for the accommodation of local incompatibilities of strain, for instance at sample–piston interfaces (full contact, stages II and III). The latter are actually expected, because twinning is not isotropic and the pistons do not have enough degrees of freedom to fit the heterogeneous sample strain if it solely results from twinning. For these reasons, retrieving the real Young modulus was not possible; therefore, only an apparent and much lower modulus than the expected value was estimated for calcite. Stage (II), which corresponds to a pseudo-elastic deformation period, combines both the elastic deformation of the material and that of the loading frame (made of aluminium). The plastic yield strength is reached when twinning activation starts. The latter is evidenced by the change in the slope of the stress–strain curve. Beyond this threshold, deformation stage (IIIa) is characterized by strong strain hardening, which is related to increasing twinning activation and slight densification of twin lamellae. Stage (IIIb) is the second phase of twinning-related plastic deformation, with a strong increase in twin density and substantial lamellae spreading and thickening. At this last stage, the stress–strain curve is strongly serrated, and made of segments of strain hardening followed by sudden stress drops, leading to the formation of a plateau-like stress–strain curve. Both stages IIIa and IIIb partly involve micro-cracking as a secondary deformation mechanism, although this remained limited and never propagated throughout the whole specimen before it reached several percent shortening due to dominant twinning.
3.2.2 Relationship between macroscopic behavior and microstructures
During stage (II) deformation is essentially elastic, and there is no development of any specific microstructure. The following plastic domain is evidenced by the appearance of the first twin lamellae during stage IIIa and by further twin densification and thickening during stage IIIb. Stage IIIa may also exhibit some minor micro-cracks that are very localized and do not cross throughout the crystal. Such behavior could have been avoided by applying confining pressure or by allowing for lateral free displacements of the pistons. The first isolated twin lamellae appeared during stage (IIIa). This early twinning stage is characterized by strain hardening and lasts up to 1 %–1.5 % shortening. The final plastic stage IIIb occurred for further loading. During the deformation at nearly steady-state flow stress (plateau-like stress–strain curve) two phenomena were observed for all of the samples: (1) densification of twin lamellae in bursts, and (2) thickening of twin lamellae in bursts. In general, the twin lamellae that formed near the loaded sample faces did not thicken very much, whereas the twin lamellae forming at the central portion of the crystals could reach up to 90 µm in thickness. Thickening occurred in the following sequence: (1) densification of twinning, (2) thickening of the individual lamellae and (3) merging of thickened lamellae. The widest twin lamellae were the final result of several merging events. Some lamellae from the central part of the specimen, emerging at the free lateral surfaces, show spectacular thickening. In contrast, lamellae emerging at the sample–piston interfaces remained thinner. This difference may be due to the boundary conditions, that is to say the absence of confining pressure at the lateral free surfaces may have favored thickening, whereas the stress state and the frictions at the faces loaded by the pistons may have inhibited thickening and the merging of twin lamellae.
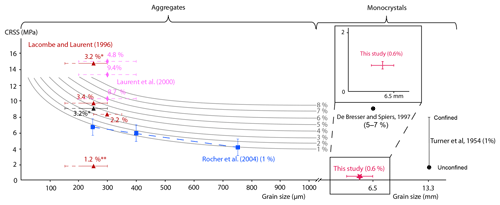
Figure 5Summary of the current knowledge about the evolution of the CRSS value as a function of grain size and strain. The figure has been modified from an initial drawing by Amrouch (2010) on the basis of data by Rocher et al. (2004). Constraints from the earlier and present studies are reported (De Bresser and Spiers, 1997; Lacombe and Laurent, 1996; Laurent et al., 2000; Turner et al., 1954). * Initial value from Lacombe and Laurent (1996) re-evaluated by Rocher (1999). Outliers due to data issues.
3.2.3 Twin lamella thickness
Twinning is a deformation mechanism that accommodates the applied bulk strain with some twin lamellae, the thickness of which is controlled by temperature (Burkhard, 1993): a given amount of strain is accommodated by a number of thin twins at temperatures lower than 170–200 ∘C and by fewer but thicker twins at temperatures above this range (e.g., Ferrill, 1991, 1998). Calcite twin lamellae are usually considered thick when they exceed 2–5 µm. Rybacki et al. (2013) called this statement into question by documenting 3 µm-thick twin lamellae during their experiments at room temperature. Our experiments confirm their findings in that the duration of stress application, and hence the resulting strain, has a significant impact on twin lamella thickness even at low temperature. This means that calcite twin morphology (e.g., thickness) cannot be used as a straightforward low-temperature deformation geothermometer (Ferrill et al., 2004).
However, the large amount of thickening (up to 90 µm) observed during our experiments is likely due to the lack of confining pressure and/or the free surfaces of the samples. This means that our results cannot currently be directly and easily extrapolated to natural aggregates. Actually, confining the samples with a fluid, or leaving an unconfined free surface during uniaxial compression, could affect twin thickening with respect to confinement by crystalline grains. In the latter case, within a polycrystal, the crystallographic orientation of the neighbors will greatly condition the amount of crystal shear that can be transmitted across the grain boundaries. The crystallographic constraints, in terms of shear strain compatibility, along the grain boundaries would favor the occurrence of numerous distributed thin twins. Conversely, the presence of fluid confined free surfaces could favor the localized development of thick twins. Following our reasoning, in highly porous carbonate rocks, most of the constitutive calcite grains offer free surfaces to the porous space. In other words, most of the grains are only partly constrained by neighboring grains. Stress enhancement at grain-to-grain contacts and the presence of unconstrained surfaces at pore spaces possibly facilitate activation and development of thick twin lamellae.
3.2.4 CRSS value
One goal of this study was to constrain the evolution of the CRSS value as a function of grain size. In commonly encountered reservoir carbonate rocks (particularly oolitic rocks), the mean grain size is usually lower than 1 mm. In this study, the single-crystal samples were necessarily much bigger; therefore, the results may not be able to be directly extrapolated to natural aggregates. The evolution of the CRSS value with grain size is suggested to follow the Hall–Petch equation (Covey-Crump et al., 2017). Figure 5 summarizes the results of previous studies regarding the evolution of the CRSS value vs. grain size. The CRSS values determined during this study were in the predicted asymptotic part of the curve, so no clear trend can be derived for millimeter-sized grains.
Defining the CRSS for twinning activation is not straightforward, and continuous monitoring of the experiment is required. In this study, two grain sizes were tested: and mm3. These grain sizes are not often encountered in natural rocks. From these analyses, the CRSS value was found to be around 0.90 pm0.35 MPa (Fig. 5). These values are very low compared to previous studies (De Bresser and Spiers, 1997; Turner et al., 1954), except for the unconfined samples from Turner et al. (1954) (Fig. 5). However, it is worth mentioning that a direct comparison of our results with those from other similar studies is not easy for several reasons:
-
Turner et al. (1954) used natural Icelandic spars. We show (Supplement) that we also used Island spars for establishing the experimental protocol. However, the results are not directly comparable with those obtained from the synthetic (optical quality) crystals. As previously stated, the natural calcite single crystals are already slightly strained (some twins are visible), or cleaved, and most contain micro-fluid inclusions. All of these defects induced strain hardening during the experiments, and likely increased the determined CRSS values for twinning activation (see Figs. S2, S3 and S4 in the Supplement). This is the likely reason why, as expected, our synthetic samples provide a CRSS value slightly lower than those of Turner et al. (1954). Overall, using natural samples implies starting from an undefined initial state, which calls the validity of the retrieved CRSS values into question.
-
De Bresser and Spiers (1997) annealed their Icelandic spar specimens in order to restore the previous cumulated strain. Unfortunately, as previously explained, this procedure leads to the formation of subgrain boundaries, which affect the propagation and spreading of twins and cause non-uniform stress distribution at the grain scale, potentially biasing the results.
Moreover, for both of these previous studies, the determination of the CRSS was based on post mortem observations, which precludes accounting for the loading history and probably the detection of the earliest twinning events. Other possible issues deal with the likely influence of the crystal chemistry and the starting defect density which might affect the lattice structure, and requires further investigation.
Some questions also arise regarding the CRSS value determined from the macroscopic behavior, i.e., whether the CRSS value should be considered at the appearance of the first isolated twin lamella or at the “plateau” marked by the densification and thickening of twin lamellae.
Finally, as in the case of twin thickening, another point is the extent to which CRSS values determined from single crystals may be extrapolated to an aggregate, assuming that the grain size is homogeneous and similar to that of the single crystals from which the CRSS was determined. Again, the quantitative characteristics of twinning in a single crystal may not be directly and easily transposed to what happens in twinning grains within an aggregate. Indeed, as previously mentioned, grain boundaries are obstacles to twin propagation and twinning requires additional deformation mechanisms that ensure shear strain compatibilities between adjacent grains, as twinning plasticity is inherently anisotropic. The application of mechanical data gathered on single crystals to an aggregate thus remains an issue. For this reason, analytical mean field or computational full field homogenization models must be applied to try and predict calcite aggregate behaviors. This is far beyond the scope of the present work, which essentially provides the basic input for further homogenization modeling.
The macroscopic behavior shown on direct observations of single calcite crystals deformed uniaxially at room temperature was tightly correlated with the development of twinning microstructures. The study shows (1) the early onset of crystal plasticity with the activation of the very first isolated mechanical twins during the strain hardening (stage II), and (2) the densification and thickening of twin lamellae during the final stage. The latter accounts for most of the irreversible strain and corresponds to episodically fluctuating crystal strength, with strain hardening increments followed by equivalent stress drops related to twinning events.
Thickening of twin lamellae occurs in two steps with increasing deformation: (1) thickening of the individual lamellae and (2) merging of thickened lamellae. Our observations of thickening of twins at a low temperature confirm recent results obtained by Rybacki et al. (2013).
The different values of the CRSS (i.e., 0.90±0.35 MPa) for the activation of isolated twins and for the onset of densification and thickening in our deformed samples raises questions about the appropriate value to consider when using calcite twins for inversion purposes aimed at retrieving paleostress orientations and magnitudes (e.g., Lacombe, 2007, 2010; Parlangeau et al., 2018). Furthermore, we did not see any clear grain-size effect on the CRSS value. Therefore, one may wonder whether this may reflect the expected asymptotic evolution of the CRSS with large grain size as predicted by the Hall–Petch relation.
The additional occurrence of micro-cracking events suggests either imperfections in the sample geometry or the need for complementary and concomitant accommodation mechanisms due to twinning anisotropy. These observations highlight the importance of direct observations during mechanical testing in order to interpret mechanical data.
Finally, our results cannot currently be directly and easily extrapolated to natural aggregates. The application of mechanical data gathered on single crystals to an aggregate is another important topic to be addressed in the future. Nevertheless, the reported preliminary results pave the way to more confident investigations of different grain sizes and of both natural and synthetic aggregates.
Data are accessible by contacting Camille Parlangeau by email (camille.parlangeau@gmail.com).
The supplement related to this article is available online at: https://doi.org/10.5194/se-10-307-2019-supplement.
The authors declare that they have no conflict of interest.
This study is part of Camille Parlangeau's PhD work conducted at the
Institut des Sciences de la Terre de Paris (ISTeP) of Sorbonne
Université and IFP Energies Nouvelles, and supported by IFP Energies
Nouvelles. The purchase of synthetic single crystals was made possible via a
grant provided by the LABEX Matisse (Sorbonne Université, IFP Energies
Nouvelles). The experiments were financially supported by the LMS-Ecole
Polytechnique and the Chaire Energies Durables (EDF foundation).
Camille Parlangeau warmly thanks Eric Kohler and Sylvie Schueller for their help and
fruitful advice. The authors thank Hans de Bresser and an anonymous
reviewer for their thoughtful comments that helped improve the initial
version of the paper.
Edited by: Michael Heap
Reviewed by: Hans de Bresser and one anonymous referee
Amrouch, K.: Apport de l'analyse microstructurale à la compréhension des mécanismes de plissement, Exemples de structures plissées aux USA (Wyoming) et en Iran (Zagros), unpublished PhD, Université Pierre et Marie Curie-Paris 6, 477 pp., 2010.
Bornert, M., Valès, F., Gharbi, H., and Nguyen Minh, D.: Multiscale full-field strain measurements for micromechanical investigations of the hydromechanical behaviour of Clayey rocks, Strain, 46, 33–46, https://doi.org/10.1111/j.1475-1305.2008.00590.x, 2010.
Burkhard, M.: Calcite twins, their geometry, appearance and significance as stress-strain markers and indicators of tectonic regime: a review, J. Struct. Geol., 15, 351–368, https://doi.org/10.1016/0191-8141(93)90132-T, 1993.
Cover-Crump, S. J., Schofield, P. F., and Oliver, E. C.: Using neutron diffraction to examine the onset of mechanical twinning in calcite rocks, J. Struct. Geol., 100, 77–97, https://doi.org/10.1016/j.jsg.2017.05.009, 2017.
De Bresser, J. H. P. and Spiers, C. J.: Slip systems in calcite single crystals deformed at 300–800 ∘C, J. Geophys. Res., 98, 6397–6409, https://doi.org/10.1029/92JB02044, 1993.
De Bresser, J. H. P. and Spiers, C. J.: Strength characteristics of the r, f, and c slip systems in calcite, Tectonophysics, 272, 1–23, https://doi.org/10.1016/S0040-1951(96)00273-9, 1997.
Ferrill, D. A.: Calcite twin widths and intensities as metamorphic indicators in natural low-temperature deformation of limestone, J. Struct. Geol., 13, 667–675, https://doi.org/10.1016/0191-8141(91)90029-I, 1991.
Ferrill, D. A.: Critical re-evaluation of differential stress estimates from calcite twins in coarse-grained limestone, Tectonophysics, 285, 77–86, https://doi.org/10.1016/S0040-1951(97)00190-X, 1998.
Ferrill, D. A., Morris, A. P., Evans, M. A., Burkhard, M., Groshong, R. H., and Onasch, C. M.: Calcite twin morphology: a low-temperature deformation geothermometer, J. Struct. Geol., 26, 1521–1529, https://doi.org/10.1016/j.jsg.2003.11.028, 2004.
Friedman, M. and Heard, H. C.: Principal stress ratios in cretaceous limestones from Texas gulf coast, Am. Assoc. Petr. Geol. B., 58, 71–78, https://doi.org/10.1306/83D9137B-16C7-11D7-8645000102C1865D, 1974.
Griggs, D. and Miller, W. B.: Deformation of Yule marble: part I-Compression and extension experiments on dry Yule marble at 10,000 atmospheres confining pressure, room temperature, Bull. Geol. Soc. Am., 62, 853–882, https://doi.org/10.1130/0016-7606(1951)62[853:DOYMPI]2.0.CO;2, 1951.
Griggs, D., Turner, F., Borg, I., and Sosoka, J.: Deformation of Yule marble: part IV-Effects at 150 ∘C, Bull. Geol. Soc. Am., 62, 1385–1406, https://doi.org/10.1130/0016-7606(1951)62[1385:DOYMPI]2.0.CO;2, 1951.
Griggs, D., Turner, F., Borg, I., and Sosoka, J.: Deformation of Yule marble: part V-Effects at 300 ∘C, Bull. Geol. Soc. Am., 64, 1327–1342, https://doi.org/10.1130/0016-7606(1953)64[1327:DOYMPV]2.0.CO;2, 1953.
Handin, J. and Griggs, D.: Deformation of Yule marble: part II-Predicted fabric changes, Bull. Geol. Soc. Am., 62, 863–886, https://doi.org/10.1130/0016-7606(1951)62[863:DOYMPI]2.0.CO;2, 1951.
Lacombe, O.: Paleostress magnitudes associated with development of mountain belts: Insights from tectonic analyses of calcite twins in the Taiwan foothills, Tectonics, 20, 834–849, https://doi.org/10.1029/2001TC900019, 2001.
Lacombe, O.: Comparison of paleostress magnitudes from calcite twins with contemporary stress magnitudes and frictional sliding criteria in the continental crust: Mechanical implications, J. Struct. Geol., 29, 86–99, https://doi.org/10.1016/j.jsg.2006.08.009, 2007.
Lacombe, O.: Calcite twins, a tool for tectonic studies in thrust belts and stable orogenic forelands, Oil and Gas Science and Technology, 65, 809–838, https://doi.org/10.2516/ogst/2009088, 2010.
Lacombe, O. and Laurent, P.: Determination of deviatoric stress tensors based on inversion of calcite twin data from experimentally deformed monophase samples: preliminary results, Tectonophysics, 255, 189–202, https://doi.org/10.1016/0040-1951(95)00136-0, 1996.
Laurent, P., Kern, H., and Lacombe, O.: Determination of deviatoric stress tensors based on inversion of calcite twin data from experimentally deformed monophase samples, Part II. Axial and triaxial stress experiments, Tectonophysics, 327, 131–148, https://doi.org/10.1016/S0040-1951(00)00165-7, 2000.
Newman, J.: The influence of grain size and grain size distribution on methods for estimating paleostresses from twinning in carbonates, J. Struct. Geol., 16, 1589–1601, https://doi.org/10.1016/0191-8141(94)90129-5, 1994.
Parlangeau, C., Lacombe, O., Schueller, S., and Daniel, J.-M.: Inversion of calcite twin data for paleostress orientations and magnitudes: a new technique tested and calibrated on numerically-generated and natural data, Tectonophysics, 722, 462–485, https://doi.org/10.1016/j.tecto.2017.09.023, 2018.
Rocher, M.: Déformations et paléocontraintes des avant-pays de chaînes de collision: les piedsmonts occidentaux de Taïwan et le bassin Sud-Aquitain, unpublished Ph.D, Université Pierre et Marie Curie-Paris 6, 461 pp., 1999.
Rocher, M., Cushing, M., Lemeille, F., Lozac'h, Y., and Angelier, J.: Intraplate paleostresses reconstructed with calcite twinning and faulting: improved method and application to the eastern Paris Basin (Lorraine, France), Tectonophysics, 387, 1–21, https://doi.org/10.1016/j.tecto.2004.03.002, 2004.
Rowe, K. J. and Rutter, E. H.: Palaeostress estimation using calcite twinning: experimental calibration and application to nature, J. Struct. Geol., 12, 1–17, https://doi.org/10.1016/0191-8141(90)90044-Y, 1990.
Rybacki, E., Evans, B., Janssen, C., Wirth, R., and Dresen, G.: Influence of stress, temperature, and strain on calcite twins constrained by deformation experiments, Tectonophysics, 601, 20–36, https://doi.org/10.1016/j.tecto.2013.04.021, 2013.
Schmid, S. M. and Paterson, M. S.: Strain analysis in an experimentally deformed oolitic limestone, in: Energetics of Geological Processes, edited by: Saxena, S. K., Bhattacharji, S., Annersten, H., and Stephansson, O., Springer, Berlin, Heidelberg, https://doi.org/10.1007/978-3-642-86574-9_5, 1977.
Tullis, T. E.: The use of mechanical twinning in minerals as a measure of shear stress magnitudes, J. Geophys. Res., 85, 6263–6268, https://doi.org/10.1029/JB085iB11p06263, 1980.
Turner, F.: Preferred orientation of calcite in Yule marble, Am. J. Sci., 247, 593–621, https://doi.org/10.2475/ajs.247.9.593, 1949.
Turner, F. and Chi'ih, C.: Deformation of Yule marble: part III-Observed fabric changes due to deformation at 10,000 atmospheres confining pressure, room temperature, dry, Bull. Geol. Soc. Am., 62, 887–906, https://doi.org/10.1130/0016-7606(1951)62[887:DOYMPI]2.0.CO;2, 1951.
Turner, F., Griggs, D., and Heard, H.: Experimental deformation of calcite crystals, Bull. Geol. Soc. Am., 65, 883–934, https://doi.org/10.1130/0016-7606(1954)65[883:EDOCC]2.0.CO;2, 1954.