the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Can subduction initiation at a transform fault be spontaneous?
Diane Arcay
Serge Lallemand
Sarah Abecassis
Fanny Garel
We present an extensive parametric exploration of the feasibility of “spontaneous” subduction initiation, i.e., lithospheric gravitational collapse without any external forcing, at a transform fault (TF). We first seek candidates from recent subduction initiation events at an oceanic TF that could fulfill the criteria of spontaneous subduction and retain three natural cases: Izu–Bonin–Mariana, Yap, and Matthew and Hunter. We next perform an extensive exploration of conditions allowing for the spontaneous gravitational sinking of the older oceanic plate at a TF using 2-D thermomechanical simulations. Our parametric study aims at better delimiting the ranges of mechanical properties necessary to achieve the old plate sinking (OPS). The explored parameter set includes the following: crust and TF densities, brittle and ductile rheologies, and the width of the weakened region around the TF. We focus on characterizing the OPS conditions in terms of (1) the reasonable vs. unrealistic values of the mechanical parameters and (2) a comparison to modern cases of subduction initiation in a TF setting. When modeled, OPS initiates following one of two distinct modes, depending mainly on the thickness of the overlying younger plate. The asthenosphere may rise up to the surface above the sinking old plate, provided that the younger plate remains motionless (verified for ages ≥5 Myr, mode 1). For lower younger plate ages (typically ≤2 Myr), the younger plate is dragged toward the older plate, resulting in a double-sided subduction (mode 2). When triggered, spontaneous OPS is extremely fast. The parameters that exert the strongest control over whether OPS can occur or not are the brittle properties of the shallow part of the lithosphere, which affect the plate resistance to bending, the distance away from the TF over which weakening is expected, and the crust density. We find that at least one mechanical parameter has to be assigned an unrealistic value and at least two other ones must be set to extreme ranges to achieve OPS, which we do not consider realistic. Furthermore, we point out inconsistencies between the processes and consequences of lithospheric instability, as modeled in our experiments and geological observations of subduction infancy, for the three natural candidates of subduction initiation by spontaneous OPS. We conclude that spontaneous instability of the thick older plate at a TF evolving into mature subduction is an unlikely process of subduction initiation in modern Earth conditions.
- Article
(4445 KB) - Full-text XML
-
Supplement
(2768 KB) - BibTeX
- EndNote
The process of spontaneous subduction deserves to be explored again following recent discoveries during Ocean Drilling Project 375 in the backarc of the proto-Izu–Bonin subduction zone. The nature and age of the basaltic crust drilled there appeared to be similar to those of the forearc basalts underlying the boninites of the present Izu–Bonin forearc (Hickey-Vargas et al., 2018). The consequences of this discovery are controversial since they are supposed to support the concept of spontaneous subduction for some authors (Arculus et al., 2015; Stern and Gerya, 2018), whereas for other authors, they do not (Keenan and Encarnación, 2016; Lallemand, 2016).
The notion of “spontaneous subduction” originates from two observations: (1) Uyeda and Kanamori (1979) first described the Mariana-type extreme subduction mode, where an old oceanic plate sunk, driven by its weight excess into a vertical slab in association with backarc extension. (2) A few years later, in the early 1980s, Bonin Island volcanic rock analysis and deep sea drilling (Leg 60) in the adjacent Izu–Bonin–Mariana (IBM) subduction zone forearc revealed rocks called boninites that combined the characteristics of arc-lavas and MORB (Mid-ocean ridge basalt; Natland and Tarney, 1981; Bloomer and Hawkins, 1983). A conceptual model was then proposed by Stern and Bloomer (1992) reconciling these observations, in which an old plate may sink in the mantle under its weight along the weak boundary formed by a transform fault. Numerical models (Hall and Gurnis, 2003; Gurnis et al., 2004) first failed to support this process of spontaneous subduction and concluded that a tectonic force was required to initiate subduction. Later, they finally succeeded in simulating spontaneous subduction in specific contexts, such as lithospheric collapse around a plume head (Whattam and Stern, 2015) or the conjunction of a large density contrast with a very weak fault zone between the adjacent lithospheres (Leng and Gurnis, 2015).
In this study, we will adopt the definition of Stern and Gerya (2018): spontaneous subduction is caused by forces originating at the subduction initiation site and not elsewhere (Fig. 1b). They define three different settings where spontaneous subduction may develop: passive margin, transform fault (TF), or plume head. The only Cenozoic examples that were attributed by Stern and Gerya (2018) to potential sites of spontaneous subduction initiation, i.e., IBM and Tonga-Kermadec, correspond to the TF setting (Fig. 1a). In these two examples, the relics of the subduction initiation stage date back to the Eocene and are thus subject to controversy. We first recall the natural examples for which oceanic TFs or fracture zones might have evolved into a subduction zone. Then, numerical models addressing subduction initiation processes in a similar context are analyzed before developing our own numerical approach. The range of parameters allowing for spontaneous subduction initiation in our models will finally be compared with the reasonable values characterizing the natural processes.
Table 1Oceanic TFs or fracture zones, where potential subduction initiated during Cenozoic times.
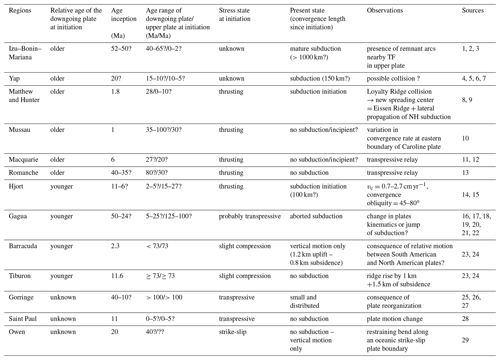
References: 1: Stern and Bloomer (1992); 2: Lallemand (2016); 3: Sdrolias and Müller (2006); 4: Gaina and Müller (2007); 5: Fujiwara et al. (2000); 6: Hawkins and Batiza (1977); 7: Hegarty and Weissel (1988); 8: Patriat et al. (2015); 9: Mortimer et al. (2014); 10: Hegarty et al. (1983); 11: Lebrun et al. (2003); 12: Meckel et al. (2005); 13: Bonatti et al. (1996); 14: Meckel et al. (2005); 15: Deschamps and Lallemand (2002); 16: Abecassis et al. (2016); 17: Deschamps et al. (2000); 18: Sibuet et al. (2002); 19: Hilde and Lee (1984); 20: Doo et al. (2015); 21: Kuo et al. (2009); 22: Eakin et al. (2015); 23: Patriat et al. (2011); 24: Pichot et al. (2012); 25: Gutscher et al. (2002); 26: Duarte et al. (2013); 27: Tortella et al. (1997); 28: Maia et al. (2016); 29: Fournier et al. (2011).
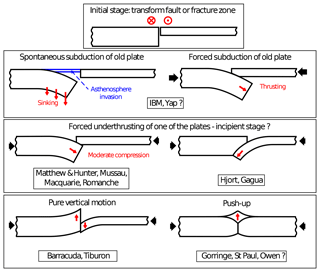
Figure 1Various tectonic settings leading to vertical motion and/or convergence at transform plate boundaries, as detailed in Table 1. The convergent black heavy arrows represent far-field tectonic forces. The red light arrows outline the sense of motion of one plate with respect to the other. The red crosses and dots in circles indicate transform motion. The thicker plate is the older one.
1.1 From oceanic transform faults or fracture zones to subduction in nature
Table 1 and Fig. 1 summarize Cenozoic settings where oceanic TFs or fracture zones underwent deformation that sometimes evolved into subduction and at other times did not. The regions are classified in Table 1 such that the older plate (OP) underthrusts the younger in the first group (Fig. 1b, c, d, IBM, Yap, Matthew and Hunter, Mussau, Macquarie, and Romanche), the downgoing plate is the youngest in the second group (Fig. 1d, e, Hjort, Gagua, Barracuda and Tiburon), and finally those for which it appears to be impossible to determine the relative age of one plate with respect to the other at the time of initiation (Fig. 1f, Gorringe, St Paul and Owen). The analysis of all these natural cases shows that the 3-D setting and far-field boundary conditions are likely to play a major role in subduction initiation and on the selected age (old/young) of the subducting plate. Earlier studies showed that compression prevailed in the upper plate at the time of initiation for most of them, while it is unknown for IBM and Yap. In these two regions, subduction started more than 20 Myr ago (Hegarty and Weissel, 1988; Ishizuka et al., 2011), but, soon after they were initiated, they underwent one of the strongest episodes of subduction erosion on Earth (Natland and Tarney, 1981; Hussong and Uyeda, 1981; Bloomer, 1983; Lallemand, 1995), so all remnants of their forearc at the time of initiation were consumed (Lallemand, 2016, and references therein). Geological evidence of the stress state at initiation is thus either subducted or deeply buried beneath the remnant Palau-Kyushu Ridge. To date, some authors (e.g., Ishizuka et al., 2018; Stern and Gerya, 2018) still argue that spreading, i.e., extension, occurred over a broad area from the backarc to the forearc at the time of subduction initiation. Backarc extension concomitant with subduction initiation under compressive stress is compatible, as exemplified by the recent case of Matthew and Hunter at the southern termination of the New Hebrides subduction zone (Patriat et al., 2015, Fig. 1d). There, the authors suggest that the collision of the Loyalty Ridge with the New Hebrides Arc induced the fragmentation of the North Fiji Basin (Eissen spreading center and Monzier rift), whose extension yielded, in turn, a compressive stress along the southern end of the transform boundary (or STEP fault), accommodating the trench rollback of the New Hebrides trench. It is important to note that the geodynamic context of the Matthew and Hunter region is very similar to the one of the IBM protosubduction (Deschamps and Lallemand, 2002, 2003; Patriat et al., 2015; Lallemand, 2016). Rifting and spreading in a direction normal to the TF has been documented at the time of subduction initiation. Since the conditions of spontaneous subduction do not require compressive stress, but rather the sinking of the oldest plate under its weight excess, and because of the lack of geological records of what happened there, we consider that IBM and Yap subduction initiation might be either spontaneous (Fig. 1b) or forced (Fig. 1c). To decipher between these two hypotheses, we conduct a series of numerical simulations.
1.2 Modeling of spontaneous subduction initiation at a transform fault in previous studies
Numerical experiments have shown that old plate sinking (OPS) could spontaneously occur for a limited viscosity contrast between lithospheres and the underlying asthenosphere (Matsumoto and Tomoda, 1983) in a model neglecting thermal effects. However, without imposed convergence, subduction initiation failed when thermal diffusion was taken into account, even in the most favorable case of an old and thick plate facing a section of asthenosphere (Hall and Gurnis, 2003; Baes and Sobolev, 2017), unless the density offset at the TF was emphasized by including a thick and buoyant crust at the younger plate (YP) surface (Leng and Gurnis, 2015). In most cases showing the instability of the thick plate, lateral density contrasts at the TF are maximized by imposing at the TF an extremely thin younger plate (0 or 1 Myr old at the location where instability initiates) in front of a thicker plate, whose age is chosen between 40 and 100 Myr, either in 2-D (Nikolaeva et al., 2008) or 3-D (Zhu et al., 2009, 2011; Zhou et al., 2018). For similar plate age pairs, Gerya et al. (2008) showed that successful spontaneous initiation requires the OP slab surface to be sufficiently lubricated and strongly weakened by metasomatism to decouple the two adjacent plates as plate sinking proceeds, while the dry mantle is supposed to be moderately resistant to bending. Assuming such “weak” rheological structure, OPS triggering occurs and results in an asthenosphere rise in the vicinity of the subduction hinge, which yields a fast spreading (from a few centimeters per year to >1 m yr−1). It has been described as a “catastrophic” subduction initiation (Hall and Gurnis, 2003). This catastrophic aspect is hampered when thicker YPs are considered (10 to 20 Myr old), when crustal and mantle rheologies are less weak, and when shallow plate weakening develops progressively through time, e.g., by pore fluid pressure increase with sea water downward percolation in a low-permeability matrix (Dymkova and Gerya, 2013).
These previous numerical studies have helped to unravel the conditions leading to OPS without any imposed external forcing. Nevertheless, recent incipient subduction zones, the most likely to correspond to initiation by spontaneous sinking at a TF, are not all associated with a significant plate age offset at plate boundaries (Matthew and Hunter, Yap, Table 1). We thus propose a new investigation of the conditions of OPS to address the following three questions. What are the mechanical parameter ranges allowing for OPS, especially for the TF settings that are the closest to spontaneous subduction conditions? Are these parameter ranges reasonable? Are the modeled kinetics and early deformation compatible with natural cases observations?
We choose a simplified setup, without fluid percolation simulations and in 2-D, to allow for a broad parameter exploration with an accurate numerical resolution.
The numerical model solves the momentum, energy, and mass conservation equations, assuming that rocks are incompressible, except for the thermal buoyancy term in the momentum equation and for the adiabatic heating term in the energy equation (extended Boussinesq approximation). As shear heating has been shown to significantly improve strain localization within the subduction interface (Doin and Henry, 2001; Thielmann and Kaus, 2012), it is included in the heat conservation equation, as well as a uniform heat production (Table 2). The simulation box, 2220 km wide and 555 km thick, is chosen to be large enough to simulate convective interactions between shallow lithospheres and deep mantle that may be involved in the process of subduction initiation (Fig. 2).
Density (ρ) is assumed to be temperature and composition dependent:
where ρref is the reference density at the surface, C is composition (mantle, oceanic crust, or weak material; Sect. 2.3), α is the thermal expansion coefficient, T is temperature, and Ts is the surface temperature (Table 2). For the mantle, is fixed to 3300 kg m−3, while ρref for the oceanic crust and the weak material is varied from one experiment to another (Sect. 2.4).
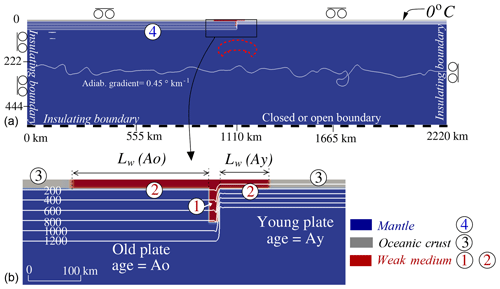
Figure 2(a) Boundary conditions, initial thermal state, and material distribution at simulation start. One white isotherm every 200 ∘C. If the box bottom is open, a vertical resistance against flow is imposed to simulate a viscosity jump approximately 10 times higher below the simulation box (Ribe and Christensen, 1994; Arcay, 2012). The red dotted line represents the hot thermal anomaly ( ∘C) imposed in some experiments. (b) Close-up on the TF structure. Lw is the width at the surface of the younger plate and of the older plate (aged of Ay and of Ao Myr, respectively) over which the oceanic crust is assumed to have been altered and weakened by the TF activity. The meaning of labels 1 to 4 is given in Sect. 2.3.
2.1 Rheology
We combine a pseudo-brittle rheology to a non-Newtonian ductile law. Pseudo-brittle rheology is modeled using a yield stress, τy, increasing with depth, z:
where C0 is the cohesive strength at the surface (Table 2), γ is a function of composition C, ρ is density, and g is the gravity acceleration. The parameter γ represents the yield strength increase with depth and can be related to the coefficient of internal friction of the Coulomb–Navier criterion (Sect. 2.5). To simplify, we tag γ as the brittle parameter. The relationship between the lithostatic pressure ρgz and the normal stress σn applied on the brittle fault will be derived in Sect. 2.5.1. The brittle deviatoric strain rate is computed assuming the following relationship (Doin and Henry, 2001): , where is the second invariant of the deviatoric strain rate tensor, is a reference strain rate, and np is a large exponent (Table 2). In the plastic domain, strain rates are close to zero if τ≪τy but become very large as soon as stress exceeds the yield stress τy. Recalling that , the plastic viscosity, νb, is written as follows:
A dislocation creep rheology is simulated using a non-Newtonian viscosity νd, defined by
where B0 is a pre-exponential factor, Ea is the activation energy depending on composition C, Va is the activation volume, n is the non-Newtonian exponent, and R is the ideal gas constant (Table 2). The effective viscosity νeff is computed assuming that the total deformation is the sum of brittle and ductile deformations. Note that the brittle behavior acts as a maximum viscosity cutoff. Regarding strain rate, a minimum cutoff is set to s−1, but no maximum cutoff is imposed.
Table 3List of simulations quoted in the text. See the data in the Supplement for the complete simulation list.
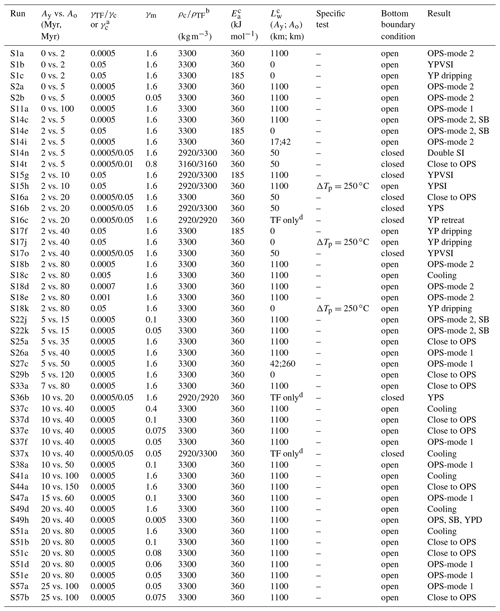
a If one value only is indicated, the oceanic crust (3) in Fig. 2 is assumed to have the same brittle parameter as the weak material forming domains (1) and (2). b If only one value indicated, then ρc=ρTF. c When one value only is indicated, Lw is identical on both plates. d The weak material is imposed at the fault zone (1) only (Fig. 2). “tw”: thermal transition width at the plate boundary. ΔTp: temperature anomaly within the plume head. νref: reference viscosity at the lithosphere–asthenosphere boundary (2.74×1019 Pa s−1). OPS: older plate sinking. YPVSI: YP vertical subduction initiation (as in Fig. 5.6). YP retreat: backward drift of the younger plate, as sketched in Fig. 4.3. YPS: younger plate sinking, as sketched in Fig. 4.4b. Double SI: double subduction initiation (as in Fig. 4.5). SB: slab break off. YPD: young plate dragging and sinking into the mantle.
2.2 Initial thermal structure and boundary conditions
We investigate a wide range of lithosphere age pairs, the younger plate (YP) age, Ay, varying from 0 to 40 Myr, and the older plate (OP) age, Ao, from 5 to 150 Myr (Table 3), to cover the plate age ranges observed in nature (Table 1). The thickness of a lithosphere is here defined by the depth of the 1200 ∘C isotherm, zLB(A), classically estimated using the half-space cooling model (Turcotte and Schubert, 1982) by
where κ is the thermal diffusivity (Table 2) and A is the plate age. However, the half-space cooling model, as well as some variations of it such as the global median heat flow model (GDH1; Stein and Stein, 1992), have been questioned (Doin et al., 1996; Dumoulin et al., 2001; Hasterok, 2013; Qiuming, 2016). Indeed, such conductive cooling models predict too cold young oceanic plates (by ∼100 to 200 ∘C) compared to the thermal structure inferred from high-resolution shear wave velocities, such as in the vicinity of the East Pacific Rise (Harmon et al., 2009). Similarly, worldwide subsidence of young seafloors is best modeled by taking into account, in addition to a purely lithosphere conductive cooling model, a dynamic component, likely related to the underlying mantle dynamics (Adam et al., 2015). Recently, Grose and Afonso (2013) have proposed an original and comprehensive model for oceanic plate cooling, which accurately reproduces the distribution of heat flow and topography as a function of seafloor age. This approach leads to young plates (<50 Myr) 100 to 200 ∘C hotter than predicted using the half-space cooling and Parsons and Sclater (1977) models, especially in the shallowest part of the lithosphere. This discrepancy notably comes from, first, heat removal in the vicinity of the ridge by hydrothermal circulation and, second, the presence of an oceanic crust on top of the lithospheric mantle that insulates it from the cold (0 ∘C) surface and slows down its cooling and thickening. Taking into account these two processes reduces the surface heat flows predicted by the GDH1 model by 75 % (Grose and Afonso, 2013). Our study focuses on young oceanic plates that are the most frequent at TFs (Ay≲60 Myr, Table 1). Therefore, we calculate lithospheric thicknesses zLB(A) as 0.75 of the ones predicted by half-space cooling model. Moreover, plates warmer than predicted by the half-space cooling model are consistent with the hypothesis of small-scale convection occurring at the base of very young oceanic lithospheres, i.e., younger than a threshold encompassed between 5 and 35 Myr (Buck and Parmentier, 1986; Morency et al., 2005; Afonso et al., 2008). An early small-scale convection process would explain short-wavelength gravimetric undulations in the plate motion direction in the central Pacific and east-central Indian oceans detected at plate ages older than 10 Myr (e.g., Haxby and Weissel, 1986; Cazenave et al., 1987). Buck and Parmentier (1986) have shown that the factor in Eq. (5) must be replaced by a value encompassed between 0.74 and 0.93 to fit the plate thicknesses simulated when early small-scale convection is modeled, depending on the assumed asthenospheric viscosity. This is equivalent to applying a corrective factor between 0.74/1.16–0.64 and 0.93/1.16–0.80, which is consistent with the lithosphere thicknesses inferred from heat flow modeling by Grose and Afonso (2013). Between the surface and zLB(A), the thermal gradient is constant.
The transform fault, located at the middle of the box top (x=1110 km), is modeled by a stair-step function joining the isotherms of the adjacent lithospheres (Fig. 2). We test the effect of the TF thermal state, which should be cooled by conduction in the case of an inactive fracture zone, in a few simulations (Sect. 3.3).
Moreover, we test the possible influence of the asthenospheric thermal state at initiation, either uniform over the whole box or locally marked by thermal anomalies resulting from the small-scale convection observed in a preliminary computation of mantle thermal equilibrium (Fig. 2). The results show that the process of subduction initiation, in the case of success or failure, does not significantly depend on the average asthenospheric thermal structure. Nevertheless, in a few experiments, we impose at the start of simulation a thermal anomaly mimicking a small plume head ascending right below the TF, 200 km wide and ∼75 km high, whose top is located at 110 km depth at start of simulation (Fig. 2). The plume thermal anomaly ΔTplume is set to 250 ∘C (Table 3). Regarding boundary conditions, slip is free at the surface and along vertical sides. We test the effect of the box bottom condition, either closed and free-slip or open to mantle in- and outflows. When the box bottom is open, a vertical resistance against flow is imposed along the box base, mimicking a viscosity jump 10 times higher than above (Ribe and Christensen, 1994; Arcay, 2017). The results show that the bottom mechanical condition does not modify the future evolution of the fracture zone. The thermal boundary conditions are depicted in Fig. 2.
2.3 Lithological structure at simulation start
The TF lithological structure is here simplified by considering three different lithologies only: the vertical layer forming the fault zone between the two oceanic lithospheres (label 1 in Fig. 2) and assumed to be the weakest material in the box, the oceanic crust (label 3), and the mantle (label 4). In all experiments, the Moho depth is set to 8.3 km for both oceanic lithospheres, and the width of the vertical weak zone forming the fault 1 is equal to 8.3 km. The depth of the weak vertical zone 1 depends on the chosen older plate age, Ao: it is adjusted to be a bit shallower than the OP base, by ∼15 to 30 km. Furthermore, we want to test the effect of the lateral extent of this weakening, outside the gouge fault, Lw (label 2 in Fig. 2). Indeed, depending on the type of TF, the weak zone width may be limited to ∼8 km, such as for the Discovery and Kane faults (Searle, 1983; Detrick and Purdy, 1980; Wolfson-Schwehr et al., 2014), implying Lw=0 km in our model or, in contrast, that the weak zone width may reach 20 to 30 km, such as for the Quebrada or Gofar TFs (Searle, 1983; Fox and Gallo, 1983); thus, Lw can be varied up to 22 km. In most experiments, we impose the same value for the lateral extent of crust weakening on both lithospheres: Lw(Ao)=Lw(Ay), except in a few simulations.
2.4 Parametric study derived from force balance
The first-order forces driving and resisting subduction initiation at a transform fault indicate which mechanical parameters would be worth testing to study OPS triggering. Without any external forcing, the unique driving force to consider is (1) the plate weight excess relative to the underlying mantle. Subduction is hampered by (2) plate resistance to deformation and bending; (3) the TF resistance to shearing; and (4) the asthenosphere strength, resisting plate sinking (e.g., McKenzie, 1977; Cloetingh et al., 1989; Mueller and Phillips, 1991; Gurnis et al., 2004). We vary the mechanical properties of the different lithologies forming the TF area to alter the incipient subduction force balance. The negative plate buoyancy (1) is related to the plate density, here dependent only on the thermal structure and plate age A (Sect. 2.2) since we do not explicitly model density increase of metamorphized (eclogitized) oceanic crust. Nonetheless, we vary the crust density, ρc, imposed at the start of simulation along the plate surface to test the potential effect on plate sinking. We also investigate how the density of the weak layer forming the interplate contact, ρTF, which is not well known, may either resist plate sinking (if buoyant) or promote it (if dense). The plate strength and flexural rigidity (2) are varied in our model by playing on different parameters. First, we test the rheological properties of the crustal layer both in the brittle and ductile realms, by varying γc and (Eqs. 2 and 4). Second, the lithospheric mantle strength is varied through the mantle brittle parameter, γm, that controls the maximum lithospheric stress in our model. Third, we vary the lateral extent (Lw) of the shallow lithosphere weakened domain, related to the crust alteration likely to occur in the vicinity of the TF.
We study separately the influence of these six mechanical parameters (ρc, ρTF, γc, , γm, Lw) for most plate age pairs. The TF strength (3) is often assumed to be quite low at the interplate contact (Gurnis et al., 2004; Gerya et al., 2008). We thus fill the TF “gouge” with the weak material (labeled 1 in Fig. 2) and, in most experiments, set it as . In some experiments, we replace the weak material filling the TF gouge by the more classical oceanic crust (labeled 3 in Fig. 2) to test the effect of a stiffer fault. In that case, and Lw=0 km: the TF and both plate surfaces are made of gabbroic oceanic crust (Table 3). Note that when , the weak layer and the oceanic crust are mechanically identical, and the weak layer then entirely covers the whole plate surface (Lw=1100 km). Similarly, as the activation energy is the same for the oceanic crust and the weak material, assuming a low ductile strength for the TF is equivalent to covering the whole plate surface by the weak layer (setting Lw=1100 km).
Apart from the six main physical properties that are repeatedly tested (Sect. 2.5), we perform additional experiments for a limited number of plate age combinations to investigate a few extra parameters. In this set of simulations, we vary the asthenosphere resistance competing against plate sinking (4), either by changing the asthenospheric reference viscosity at the lithosphere base or by inserting a warm thermal anomaly simulating an ascending plume head (Fig. 2). We also test the influence of the lithosphere ductile strength that should modulate plate resistance to bending (2) by varying the mantle activation energy, . At last, we further explore the TF mechanical structure (3) by imposing an increased width of the TF weak gouge, and different thermal structures of the plate boundary forming the TF.
2.5 Ranges of investigated physical properties
2.5.1 Brittle properties for oceanic crust, transform fault and mantle lithologies
The brittle parameter γ in Eq. (2) is related to the tectonic deviatoric stress, Δσxx, and to the lithostatic pressure, σzz (Turcotte and Schubert, 1982): Δσxx=γσzz. One may derive the relationship under compression between γ and the classical coefficient of static friction, fs, defined by , where τ is the shear stress along the fault (Turcotte and Schubert, 1982):
where λ is the pore fluid pressure coefficient, ρw is the water density, and pw is the pore fluid pressure, assuming that pw=ρwgz if λ=0 and pw=ρgz if λ=1. The brittle parameter γ moderately depends on the average density in the overlying column, ρ (Fig. S1 in the Supplement). The internal friction coefficient, fs, initially considered approximately constant (fs∼0.6 to 0.85; Byerlee, 1978) is suggested to vary with composition from recent experimental data. For a dry basalt, fs would be encompassed between 0.42 and 0.6 (Rocchi et al., 2003; Violay et al., 2012). Assuming high pore fluid pressure in the oceanic crust (λ≥0.45), γc from Eq. (6) is then close to 0.8 (Fig. S1). If the oceanic crust is altered by the formation of fibrous serpentine or lizardite, fs decreases to 0.30 (Tesei et al., 2018), entailing γc∼0.05 if the pore fluid pressure is high (λ=0.9), which we consider the minimum realistic value for modeling the crustal brittle parameter (Fig. 3a). In the presence of chrysotile, fs may even be reduced to 0.12 at low temperature and pressure (Moore et al., 2004), which would reduce γc to ∼0.01 (for λ=0.9), deemed as the extreme minimum value for γc. Note that relationship between the presence of fluid and its effect on the effective brittle strength (λ value) depends on the fault network and on the degree of pore connectivity, which may be highly variable (e.g., Carlson and Herrick, 1990; Tompkins and Christensen, 1999).
Regarding the TF, the fault material is assumed to be either mechanically similar to a weak serpentinized crust (γTF=0.05) or even softer (e.g., Behn et al., 2002; Hall and Gurnis, 2005). In that case, we set .
At mantle depths, the effect of pore fluid pressure on brittle strength is more questionable than at crustal levels. To simplify, we suppose the pore fluid pressure pw to be very low, close to zero, assuming that the lithospheric mantle is dry in absence of any previous significant deformation. The coefficient of internal friction from Eq. (7) for a dry mantle decreases from fs=0.65 (Byerlee, 1978) to fs∼0.35 or 0.45 if peridotite is partly serpentinized (Raleigh and Paterson, 1965; Escartín et al., 1997), leading to γm between 2.8 and 0.8. However, assuming γm=2.8 would lead to an extremely high lithospheric strength (∼1 GPa at only 11 km depth) since our rheological model neglects other deformation mechanisms. We thus restrict the maximum γm to 1.6, which has been shown to allow for a realistic simulation of subduction force balance for steady-state subduction zones (Arcay et al., 2008). The most likely interval for γm is eventually [0.8–1.6] (Fig. 3b). The mantle brittle parameter γm might decrease to ∼0.15 (fs=0.12) if chrysotile is stable, which is nevertheless unexpected at mantle conditions. Lower γm are considered unrealistic, even if γm=0.02 has been inferred to explain plate tectonic convection (in the case of a mantle devoid of a weak crustal layer; Korenaga, 2010).
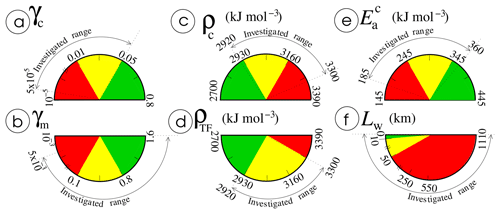
Figure 3Physical properties tested in this study and investigated ranges. (a) Brittle parameter for the oceanic crust, γc; (b) Brittle parameter for the mantle, γm; (c) Oceanic crust density, ρc; (d) Density of the weak medium forming the TF, ρTF; (e) Activation energy of the oceanic crust, , assuming a non-Newtonian exponent n=3 in Eq. (4); (f) Lateral extent of the weak domain on both flanks of the TF, Lw. The parameter intervals vary from realistic ranges (in green) to extreme values (in yellow). They are still extended beyond these values, up to unrealistic ranges to achieve the conditions allowing for spontaneous subduction (in red).
2.5.2 Crust and transform fault densities
The oceanic crust density is varied from the classical value for a wet gabbro composition in the pressure–temperature conditions prevailing at the surface (2920 kg m−3; Bousquet et al., 1997; Tetreault and Buiter, 2014). Crust density in the blueschist facies reaches 3160 kg m−3, but we try even higher densities by imposing a mantle value. This would correspond to crust eclogitization and the heaviest crust to maximize the column weight within the older plate (OP) to promote its gravitational instability (Fig. 3c). Rocks forming the fault “gouge” are likely to be vertically highly variable in composition, possibly rich in buoyant phases such as serpentine and talc close to the surface (e.g., Cannat et al., 1991) and more depleted in hydrous phases at the deeper level. Below the Moho, down to its deepest portion, the fault may be compounded of a mix between oceanic crust and altered mantle (Cannat et al., 1991; Escartín and Cannat, 1999). The density of the fault gouge is thus likely to increase from the surface toward the deeper part of the fault, from a hydrated gabbro density to a mantle density. We thus test for ρTF values spanning from a gabbroic density to a mantle one (Fig. 3d). Note that these densities correspond to reference values at surface conditions (T=0 ∘C and P=0 kbar), knowing that density is here a function of temperature through the coefficient of thermal expansion (Table 2).
2.5.3 Activation energy for the crust
The most realistic interval for the crustal activation energy can be defined from experimental estimates for an oceanic crust composition. Nonetheless, values are associated with specific power law exponent, n, in Eq. (4), while we prefer to keep n=3 in our numerical simulations for the sake of simplicity. Therefore, to infer the interval in our modeling using a non-Newtonian rheology, we assume that without external forcing, mantle flows will be comparable to sublithospheric mantle convective flows. The lithosphere thermal equilibrium obtained using a non-Newtonian rheology is equivalent to the one obtained with a Newtonian ductile law if the Newtonian Ea is equal to the non-Newtonian Ea multiplied by (Dumoulin et al., 1999). As sublithospheric small-scale convection yields strain rates by the same order of plate tectonics ( s−1; Dumoulin et al., 1999), this relationship is used to rescale the activation energies experimentally measured in our numerical setup devoid of any external forcing. We hence compute the equivalent activation energy as follows: , where ne is the experimentally defined power law exponent. The activation energy in the dislocation creep regime is encompassed between the one for a microgabbro, 497 kJ mol−1 (Wilks and Carter, 1990, with a non-Newtonian exponent ne=3.4) and the one of a dry diabase, i.e., 485±30 kJ mol−1 (Mackwell et al., 1998, with ). For a basalt, has been recently estimated to 456 kJ mol−1 (Violay et al., 2012, with ne∼3.6). Lower values inferred for other lithologies are possible but less likely, such as for a wet diorite ( kJ mol−1, ne=2.4; Ranalli, 1995), and are used to define the lower bound of the “yellow” range for (Fig. 3e). A few experiments have shown that can be as low as 132 kJ mol−1 (ne=3) if hornblende and plagioclase are present in high proportions (Yongsheng et al., 2009). This activation energy, as well as the one of a wet quartzite ( kJ mol−1, ne=2.3; Ranalli, 1995), though used in numerous thermomechanical modeling studies of subduction, is considered an unrealistic value in a TF setting. Nevertheless, a low plate ductile strength promoted by a thick crust has been suggested to favor spontaneous subduction initiation at a passive margin (Nikolaeva et al., 2010). We choose to not vary the crustal thickness but to test in a set of experiments the effect of a very low crustal activation energy instead (equal to 185 kJ mol−3, Fig. 3e).
2.5.4 Distance from the transform fault of crust weakening
Regarding the lateral extent of the weak material, Lw, we test values in agreement with the observed large or relatively small TFs (Lw≤20 km, as described in the previous section) and increase them up to the extreme value of 50 km (Fig. 3f). The simulation results prompt us to perform experiments in which both lithospheres are entirely covered by the weak layer (Lw∼1110 km) to achieve the conditions of spontaneous subduction initiation.
2.6 Numerical code and resolution
The models are performed using the thermo-chemo-mechanical code of convection developed by Christensen (1992), which is based on an Eulerian and spline finite element method. Conservation equations are solved to obtain two scalar fields, which are temperature and stream function (Christensen, 1984). The simulation box is discretized into 407×119 nodes. The resolution is refined in x and z directions in the area encompassing the TF, i.e., between 966 and 1380 km away from the left-hand box side, and for depths shallower than 124 km, where node spacings are set to 1.67 km. Outside the refined domain, node spacing is 10.5 km in both directions. The tracer density is uniform over the simulation box (∼3.2 per km2), verifying that at least nine tracers fill the smallest meshes. This numerical discretization has been tested and validated in a previous study (Arcay, 2017). Note that because the total pressure is not directly solved by the code in Christensen (1992), the lithostatic pressure is used instead in Eq. (4).
The original code has been adapted to allow for the simulation of three different lithologies within the simulation box (Doin and Henry, 2001; Morency and Doin, 2004): the mantle, oceanic crust, and a weak layer that would mimic an altered or hydrated and, hence, weakened region around a TF, with specific densities and rheologies (see Sect. 2.3). Composition is tracked by markers advected along flow lines using a fourth-order Runge–Kutta scheme (van Keken et al., 1997).
Here, we summarize first the experiments without OPS and then the simulations showing spontaneous gravitational instability of the OP. Next, we detail the effect of the different mechanical and geometrical parameters. Table 3 compiles the experiments explicitly quoted in the main paper. The exhaustive list of simulations performed in this study can be found in the Supplement: the experiments are compiled as a function of the plate age pair imposed at the TF in Table S1 in the Supplement, while they are ranked according to the simulated deformation regime in Table S2.
3.1 Overview of simulated behaviors other than old plate sinking
We obtain numerous behaviors different from OPS, varying as a function of (1) the plate age pair (Ay, Ao) and (2) the combination of densities, rheological parameters and the weak layer lateral extent (Lw). This large simulation set shown in Fig. 4 represents ∼73 % of the 302 experiments presented in this study, which do not show a clear OPS.
First, no tectonic deformation is modeled in many experiments, i.e., deformation only occurs within the asthenosphere below the plates but is almost totally absent at shallower depths where plate cooling takes place (Fig. 4.1). This is notably obtained if the YP is too old, that is, for Ay≥3 up to 17 Myr depending on the physical parameter set (Fig. 6).
Second, we observe the YP ductile dripping, leading to the plate dismantlement, corresponding to a series of several fast lithospheric drips, soon after the simulation start (Fig. 4.2), modeled when ductile strengths are low. The OP is not affected and solely cools through time.
Third, a transient retreat of the YP is modeled, in very few experiments, while the OP remains motionless (Fig. 4.3). This occurs if the YP is very young (Ay≤2 Myr) and if the TF density, ρTF, is low (equal to the gabbro density). Because of its buoyancy, the weak material forming the TF rises up to the surface as soon as simulation starts. This fast vertical motion (velocities ≥50 cm yr−1) is partly transmitted horizontally and deforms the weaker and younger plate, triggering a backward motion. Velocities vanish as plate cooling proceeds.
Fourth, the YP sinking is triggered in some models (Fig. 4.4). The gravitational instability of the YP is very similar to the one expected for a thick plate spontaneous sinking (as sketched in Fig. 1). The polarity of the YP sinking depends on the density imposed for the TF interface (ρTF) and on whether (or not) the weak layer covers the YP surface (Lw>0 km). The duration of YP spontaneous sinking is always very brief (<0.5 Myr): either the process does not propagate fast enough to compete against plate cooling and strengthening (Fig. 4.4b) or the diving YP segment is limited by the imposed length Lw of lithosphere recovered by the weak material (Fig. 4.4a).
Fifth, in one experiment, a double subduction initiation is observed: while YP sinking initiates, the OP also becomes unstable and starts sinking when a wider portion of weak and dense material (Lw=50 km) is included (Fig. 4.5). Nevertheless, the OP slab rapidly undergoes slab break off once the Lw long weak segment has been entirely subducted (Fig. 4.5, 0.62 Myr), which we deem as too short to represent a successful OPS initiation since the subducted slab length is limited to 50 km.
Sixth, the vertical subduction of the YP initiates at the TF when the TF material is as dense as the mantle and vertically drags the YP into the mantle (Fig. 4.6). The motion can be transmitted away from the TF up to 500 km backward but systematically entails a YP stretching at the surface, as the slab is young and soft (Ay≤7 Myr). This prevents subduction from lasting more than 1.5 Myr. Moreover, plate cooling frequently freezes the downward YP flow (Fig. 5.6, bottom row).
Finally, in ∼40 % of experiments in which OPS initiation appears to start, the process freezes up and does not evolve into a developed plate sinking. The OP bending stops very early, typically in less than ∼0.4 Myr (Fig. 4.7), especially for OP older than 80 Myr. The velocities within the OP then vanish quite fast (Fig. 4.7a). OPS also aborts even when the mechanical decoupling does occur at the TF if hot mantle flows are too slow and/or if the lateral extent of the weak material Lw is narrow (Fig. 4.7b).
3.2 Modes of OPS triggering
Spontaneous subduction is modeled when one of the two lithospheres is gravitationally unstable, which occurs if the total lateral density offset (vertically integrated) at the plate boundary is not balanced by plate, mantle, and TF resistance to deformation, as summarized in Sect. 2.4. We observe the spontaneous sinking of the OP for quite various pairs of lithosphere ages (Fig. 5), which mostly depends on the chosen set of rheological parameters and on the presence of the weak layer at the whole plate surface. When simulated, OPS occurs following one of two basic ways, later called mode 1 and mode 2. Mode 1 happens in approximately one-half of OPS cases (Fig. 5a) and is the closest to the mechanism envisioned in the spontaneous subduction concept (Fig. 1b). The mantle flow generated by the OP sinking triggers an asthenospheric upwelling focusing along the weak TF “channel” up to the surface (“asthenosphere invasion” in Fig. 1b), while the YP remains mostly motionless. The subduction process develops due to a fast hinge rollback. As mantle velocities are huge, exceeding tens of meters per year in many cases, the asthenosphere catastrophically invades the box surface, filling a domain that is soon larger than 200 km, as depicted in Fig. 5a.
In mode 2, asthenosphere invasion does not occur at the surface and is often limited to the YP Moho. Mantle flow induced by OP bending drags the YP toward the OP (Fig. 5b, c). As a consequence, a significant mass of dense crust is transferred from the top of the YP to the one of the OP, where the accumulated crust builds a crustal prism that loads the OP, amplifying its bending and sinking. This phenomenon is observed in numerous cases, systematically if the YP age is 2 Myr (Table 3), and in several cases when Ay is either 0 or 5 Myr (simulations S1a to S2b, S22j–k). In both initiation modes, velocities at the slab extremity are very high (14.6 cm yr−1 in simulation S1a, 0 vs. 2, up to ∼ 180 cm yr−1 in simulations S10a, 0 vs. 80 and S11a, 0 vs. 100). The duration to form a slab longer than ∼200 km is less than 1.5 Myr. The kinetics of the OPS process modeled in this study are consequently always very fast. This swiftness most likely comes from the significant weakness that must be imposed in our modeling setup to obtain OPS triggering (see Sect. 3.3.2).

Figure 4Illustration of the different simulated behaviors, OPS apart: close-up on the transform fault. (1) Absence of plate deformation (simulation S37x, Table 3). (2) Young plate dripping and dismantlement (simulation S17f). (3) YP retreat (simulation S16c). (4) Initiation of YP transient sinking (simulation S16b, panel a, and simulation S36b, panel b). (5) Simultaneous initiation of YP and OP sinking processes (simulation S14n). (6) Initiation of YP vertical subduction at the TF (simulation S17o). (7) OP sinking initiation that soon aborts (simulation S33a, panel a, and simulation S16a, panel b). No vertical exaggeration. The velocity scale depicted in green is specific to each simulation. The parameter boxes are color coded as a function of the investigated ranges depicted in Fig. 3.
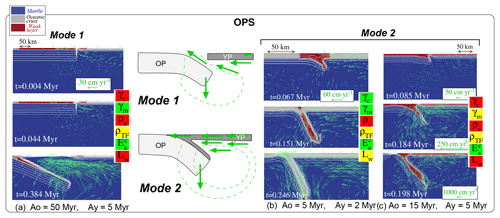
Figure 5Illustration of OPS: mode 1 in simulation S27c (panel a) vs. mode 2 in simulations S14i (panel b), and S22j (panel c). No vertical exaggeration. The parameter boxes are color coded as a function of the investigated ranges depicted in Fig. 3. Note that the velocity scale in panel (c) is specific for each snapshot. The dashed lines in the middle sketch are a schematic outline of the stream function, and the green arrows illustrate velocities.
3.3 Influence of tested parameters
The regime diagrams displayed as a function of the plate age pair (Ay,Ao) sum up our main results obtained as a function of the assumed rheological set, density field, and the lithological distribution at the surface (oceanic crust vs. TF weak material; Fig. 6). These eight regime diagrams bring out the respective influence of the main physical parameters tested in this paper, especially for deciphering conditions allowing for OPS. YP dismantlement, basically occurring when the ductile crust is softened, is not represented in the regime diagrams (discussed at the end of the section).
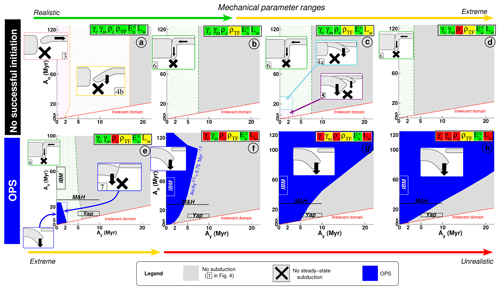
Figure 6Regime diagrams as a function of the combination of rheological properties, densities, and TF weak domain extent, Lw. “Irrelevant domain” would correspond to cases where Ay>Ao. In dotted areas, only transient behaviors, lasting less than 0.5 Myr, are modeled. Inside the inserted sketches, the numbers refer to the panel numbering in Fig. 4. The box colors correspond to parameter ranges depicted in Fig. 3. The parameter combination γc, γm, ρc, ρTF, and Lw, is, respectively, in panel (a): 0.05, 1.6, 2920, 2920 kg m−3, and 0 km; in panel (b) 0.05, 1.6, 2920 kg m−3, 3300, and 0 km; in panel (c): 0.05, 1.6, 2920, 3300 kg m−3, and 50 km; in panel (d): 0.05, 1.6, 3300, 3300 kg m−3, and 0 km; in panel (e): 0.05, 1.6, 3300, 3300 kg m−3, and 50 km; in panel (f): , 1.6, 3300, 3300 kg m−3, and 1100 km; in panel (g): , 0.1, 3300, 3300 kg m−3, and 1100 km; and in panel (h): , 0.05, 3300, 3300 kg m−3, and 1100 km. In all panels, kJ mol−1. The corresponding experiments are displayed in Fig. S2 and S3 in the Supplement. In panel (f), the boundary between the “no subduction” and “OPS” domains corresponds to the relationship Myr−1.5. When OPS is simulated (panels e to h), the conditions in Ao-Ay prevailing at subduction initiation inferred for Yap, IBM, and Matthew and Hunter (Table 1) are superimposed on the regime diagrams.
3.3.1 Transform fault and oceanic crust densities
Densities strongly affect the evolution of the TF system. If the TF weak medium is buoyant ( kg m−3), the TF material rises up to the surface forming a small and localized buoyant diapir that pushes laterally on the younger lithosphere (Fig. 4.3). The YP either shortens if it is weak enough (Ay≤2 Myr, Fig. 6a) in a backward motion or starts sinking if the YP thickness is intermediate ( Myr). On the other hand, a heavy material filling the TF gouge (ρTF=3300 kg m−3) inverts the aforementioned mechanics by pulling the YP downward at the TF to form a vertical subduction (Fig. 4.6, labeled YPVSI for “YP vertical subduction initiation” in Table 3). Note that when the fault density ρTF is very high, the oceanic crust density, ρc, buoyant or not, does not actually affect the mode of YP deformation (compare diagrams b and d in Fig. 6).
3.3.2 Lateral extent of the weak material
The results presented in Sect. 3.3.1 are obtained when the weak material is localized at the TF only (Lw=0 km). Assuming that the weak material laterally spreads out away from the TF (Lw>0 km), the mode of YP vertical subduction switches to YP sinking by gravitational instability. This is observed when young plates are modeled on both sides of the TF (Ay<5 Myr, Ao<40 Myr, Fig. 6c). The boundary between the dense weak material and the buoyant and stronger oceanic crust more or less acts as a “secondary” plate boundary, decoupling the two lithological parts of the YP, which does not occur if there is no buoyancy contrast between the crust and the weak material (Fig. 6e).
Moreover, we observe that enlarging the weak domain enables OPS in some cases if the YP is very thin (Ay≤2 Myr), regardless of the oceanic crust density (Fig. 6c, e), although OPS aborts fast, as OP subduction is limited to the weakened length Lw (set to 50 km, Fig. 6e). Simulations show that OP sinking is enhanced if Lw is much wider than expected in nature (Lw≥50 km, Fig. 3f, g, h). Otherwise, the backward propagation of bending is hindered, which stops the OPS process. We conclude that a very wide area of crust weakening on both sides of the TF is a necessary condition to simulate OPS. We quantify more accurately for different pairs of plate ages with minimum length Lw, allowing for a developed OPS in the Supplement (Sect. S2). These age pairs are selected to cover a wide range of YP ages (2 to 20 Myr). We find that the domain of weakened crust to impose in the vicinity of the TF is too large to be realistic, at least for classical mantle rheology, with the only exception being the setting with a very thin YP (Ay=2 Myr). These results suggest the strong resistant characteristic of thick YP in OPS triggering.
3.3.3 Crust brittle strength
What is the threshold in crust weakening enabling OPS? A usual value of the crust brittle parameter (γc=0.05) does not allow for OPS (Fig. 6a to e). Our simulations show that if γc is 100 times lower (), OPS can initiate for numerous plate age pairs if the whole crust is mechanically weak (Lw=1100 km, Fig. 6f) but such a brittle parameter seems unrealistic. To determine the threshold in γc allowing for OPS, we choose a high plate age offset, 2 vs. 80, the most propitious for OPS (keeping Lw=1100 km). We determine that the threshold in γc is encompassed between 10−3 and (simulations S18b, c, d, and e), which is still less than the lower bound of acceptable γc ranges (Fig. 3a). We hypothesize that for a small plate age offset, the threshold in γc would have to be even lower to observe OPS triggering.
3.3.4 Plate bending and mantle brittle parameter
Surprisingly, a very low crust brittle parameter is not sufficient for simulating OPS for some large plate age offsets, such as for (Ay,Ao) = 10 vs. 100 or 5 vs. 120 (simulations S41a and S29b, Table 3, Fig. 6f). A mechanism is thus hindering OPS. We assume that thick OPs are too strong to allow for bending. We test this by reducing the mantle brittle parameter, γm, that affects the maximum lithospheric stress in our brittle–viscous rheology, from 1.6 (Fig. 6f) to 0.1 (Fig. 6g) and 0.05 (Fig. 6h). The domain of the plate age pair where OPS can occur is then greatly enlarged toward much lower plate age offsets. We note that in most experiments showing “mantle weakening”-induced OPS, OPS stops by an early slab break off, once the infant slab reaches 200 to 300 km length because the reduced slab strength cannot sustain a significant slab pull (Fig. 5c).
In a limited set of experiments, we determine the threshold in below which OPS occurs. This threshold depends on the OP age: for the plate age pair 10 vs. 40 (simulations S37c to f) but the threshold is higher () for the plate age pair 10 vs. 50 (sim. S38a). The thicker the OP is, the easier the OPS triggering, as one may expect. We next compare experiments in which the OP and the YPs are both progressively thickened by considering the following age pairs: 10 vs. 50 (sim. S38a), 15 vs. 60 (S47a), 20 vs. 80 (S51a–e), and 25 vs. 100 (S57a–b). The experiments show that is ≥0.1, ≥0.1, ∼0.07, and ∼0.06, respectively. Hence, the plate rigidity has to be reduced as YP thickness increases, despite the joint OP thickening, down to extremely weak γm ranges (, Fig. 3). Despite the driving influence of thicker OP, thickening the YP impedes OPS in a much stronger way. Moreover, we test different means to lower the OP rigidity. For four plate age pairs for which OPS aborts (5 vs. 35, 7 vs. 70, 7 vs. 80, and 7 vs. 90), we decrease the mantle ductile strength by lowering the activation energy (Table 2) but keep constant the mantle viscosity at 100 km depth and the mantle brittle parameter (γm=1.6). We find that lowering instead of the mantle brittle parameter is much more inefficient for obtaining OPS (Table S1). Finally, our results suggest that the factors of the resistance to OPS mainly come from OP flexural rigidity and YP thickness and stiffness, in agreement with previous studies (Nikolaeva et al., 2010; Zhou et al., 2018).
3.3.5 Ductile strength decrease
The main effect of imposing a decrease in the crust and TF ductile strength (lowering to 185 kJ mol−1) is to trigger the fast dismantlement of YP by lithosphere dripping if the YP is young (Ay=2 Myr, Fig. 4.2). Otherwise, a low has no effect on the deformation of the two plates. One exception appears in simulation S14e, in which the weak ductile strength triggers mode 2 OPS. In this particular setup, both lithospheres are very thin ( vs. 5) and could be regarded as “crustal” plates because the mantle lithosphere is very thin or almost absent. In this simulation, the YP strength profile is actually similar to the other cases yielding mode 2 OPS (see Sect. S4 in the Supplement), which should explain why decreasing allows for OPS in this unique case. The YP destabilization and dripping result from the high crust density (ρc=3300 kg m−3) assumed in experiments performed with a reduced . Indeed, in experiments using a usual crustal density (ρc=2920 kg m−3), YP vertical subduction is obtained instead (simulation S15g, 2 vs. 10, for instance).
3.3.6 Plume-like thermal anomaly
The thermal anomaly simulating an ascending plume head below the TF produces effects very similar to those of a reduced : no effect if plates are older than 2 Myr and YP dismantlement if Ay=2 Myr and if the crust is dense (ρc=3300 kg m−3). Otherwise, for a normal crust density, a short stage of YP vertical subduction occurs after plume impact (2 vs. 10, simulation S15h). The hot thermal anomaly never triggers OPS in our modeling, contrary to other studies, even if we have investigated large plate age contrasts (2 vs. 40, sim. S17j, and 2 vs. 80, S18k) as well as small age offsets and plates younger than 15 Myr (Table S1). To obtain a successful plume-induced subduction initiation, it has been shown that the plume buoyancy has to exceed the local lithospheric (plastic) strength. This condition is reached either when the lithosphere friction coefficient is lower than ∼0.1 (Crameri and Tackley, 2016), and/or when the impacted lithosphere is younger than 15 Myr (Ueda et al., 2008), or when a significant magmatism-related weakening is implemented (Ueda et al., 2008) or assumed (Baes et al., 2016) in experiments reproducing modern Earth conditions. We hypothesize that if the mantle brittle parameter was sufficiently decreased, we would also achieve OPS by plume head impact. Besides, lithosphere fragmentation is observed by Ueda et al. (2008) when the plume size is relatively large in relation to the lithosphere thickness, in agreement with our simulation results showing the dismantlement for a significantly young (Ay=2 Myr) and thin lithosphere.
3.3.7 Additional tests on OPS conditions: fault gouge strength and width, transform fault vs. fracture zones, and asthenosphere viscosity
We sum up in this section the extra experiments performed to provide the precision of the mechanisms involved in OPS triggering. The detailed results are described in Sect. S3 in the Supplement. We first test the necessity of the fault softness to simulate OPS by inverting the oceanic crust and TF respective brittle parameter for models that originally displayed OPS (thus by setting for the inversion experiments: γTF=0.05, while γc=0.0005). We find that a very low TF strength is critical to model OPS.
We next wonder if OPS (when not modeled) could be triggered by widening the fault gouge from the surface to the bottom of the fault (domain 1 in Fig. 2) by setting the fault width to 20 km instead of 8.3 km in experiments that did not initially show OPS. The simulations show that OPS still does not occur, even if the mechanical decoupling is maximized (γTF decreased to ). The mechanical interplate decoupling is hence not sufficient alone to trigger OPS, at least for a 20 km wide fault.
Subsequently, we investigate the possible role of the TF thermal structure. The interplate domain is assumed to be very thin and modeled by a stair-step function (Sect. 2.2). In nature, this setup would correspond to an active transform fault. If the fault is instead inactive (fracture zone), the thermal state of the plate boundary is likely to be cooled by thermal conduction, possibly stronger and more resistant to plate decoupling. We test the effect of the TF thermal structure for the two plate age pairs for which OPS is simulated when crust weakening is assumed (γc=0.0005) by widening the TF thermal transition (from 11 up to 70 km), keeping the weak material forming the fault gouge at the center of the thermal transition in all cases. All these experiments show OPS. We here verify that the fault gouge weakening, governed by the soft material brittle properties, is independent of temperature and, at first order, is independent of the fault activity in our 2-D setup.
We finally test if a decrease in asthenosphere strength could help OPS triggering by unbalancing the OP weight excess. The experiments show that asthenospheric velocities and OP deformation are slightly amplified but still not enough to trigger OPS.
Table 4Relationship between investigated thermomechanical parameters and the main forces involved in the spontaneous subduction initiation modeled in this study. When increased from an experiment to another, the mechanical parameters are interpreted as either favoring OPS (plus sign), hampering OPS (minus sign), or not affecting OPS triggering (zero). Empty cells indicate that the relation between parameter and force cannot be inferred from our results, while a question mark means that the assumed relationship is not clear.
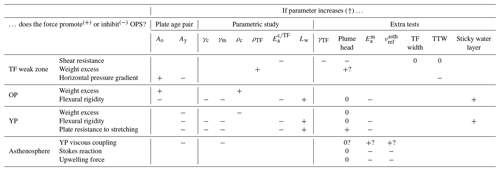
We derive the main processes involved in successful OPS triggering from the results presented in Sect. 3. In the following paragraphs, we discuss the relationship between the different thermomechanical parameters and their influence on the forces driving and resisting to OPS, which are summed up in Table 4.
4.1 OPS mode 1 vs. mode 2
The velocity fields show that modes 1 and 2 differ by the resulting YP kinematics. When mode 1 occurs, the YP remains almost motionless with respect to underlying asthenospheric flows (speeds ≤1 and ≥20 cm yr−1, respectively; see Supplement Fig. S7). In contrast, velocities during mode 2 are closer between the YP and the asthenosphere, where speeds are high (between 25 and 100 cm yr−1). Moreover, within the set of simulations showing OPS (Sect. 3.2), we find that mode 2 occurs in simulations where the YP age is 2 Myr for various rheological sets, or if Ay=5 Myr, provided that the mantle brittle strength is reduced. In all these experiments, the strength of the YP bottom part is the closest to the asthenospheric one (viscosity ratios ≲102 to 103; Fig. S8 in the Supplement). In contrast, the focusing of asthenosphere flows toward the weak TF is observed when the viscosity offset between the YP and the underlying mantle exceeds 102. We hypothesize that mode 2 results from a strong coupling between the YP and the asthenosphere, which is related to the asthenosphere ductile strength (Table 4). The particular (though not meaningful) case of Ay=0 Myr is addressed in the Supplement (Sect. S4).
The mode 2 OPS may be envisioned as an asymmetric double-sided subduction (Gerya et al., 2008, see the sketch in Fig. 5). In this subduction mode, the thick OP sinking drives the YP downward flow at the proto-slab surface because plate decoupling at shallow levels does not occur. The shallow interplate decoupling is hence not required in mode 2 since the YP is easily dragged by asthenosphere. In contrast, asthenospheric flows related to OPS in mode 1 might not be able to drag the YP because of the high viscosity offset between YP and asthenosphere . The asthenosphere upwelling along the TF (“upwelling force” in Table 4) would then result from the need to decouple the respective motions of the two plates, i.e., to accommodate OP downwelling and hinge retreat, whereas the YP is almost motionless. Simulations by Gerya et al. (2008) suggest that the thick OP lubrication by metasomatism is a way to force plate decoupling to model one-sided subduction.
4.2 Plate ages allowing for old plate sinking
The boundary between OPS and the absence of subduction can be defined for a normal mantle brittle strength γm=1.6 (Fig. 6f) using simulations in which OPS aborts (such as simulations S25a, 5 vs. 35; S29b, 5 vs. 120, or S33a, 7 vs. 80, Fig. S3 in the Supplement). We observe a dichotomy in the OPS domain boundaries. On the one hand, for thick OP (Ao>100 Myr), OPS is prevented if the YP is not extremely thin (plate age younger than 5 Myr). On the other hand, for thinner OP (Ao≤100 Myr), we experimentally show that the OPS condition corresponds to the following relationship: Myr−1.5 (Fig. 6f). In both cases, the influence of Ay is either strong or predominant. The YP age is the major determining factor in the TF evolution, compared to the OP age (separately considering the cases where the mantle brittle strength is reduced), which confirms the conclusion derived in Sect. 3.3.4 on the highly resistant effect of the YP thickness. This hindering effect results from two processes. On the one hand, high Ay ages yield low-pressure gradients across the TF due to a density contrast that decreases with YP aging (e.g., Hall and Gurnis, 2003). On the other hand, YP aging increases the YP strength competing against asthenosphere upwelling in the vicinity of the TF in OPS mode 1 and YP stretching far away from the TF to accommodate YP dragging in mode 2 (Table 4). As a result, the conditions that are the most propitious for OPS correspond to TFs, where the thinner lithosphere is as young as possible.
4.3 Parameters resisting and promoting old plate sinking
OPS is triggered if the pressure gradients at the TF related to the density offset exceed plate and mantle resistance to deformation. Density contrasts are maximized when the YP is thin, which partly explains the dominant role of the age of the YP (“proto-overriding” plate), compared to Ao, on subduction initiation, as already underlined in other studies (Nikolaeva et al., 2010; Dymkova and Gerya, 2013). Our results show that plate instability is essentially promoted by three mechanical conditions: when low brittle strengths are assumed for (1) the oceanic crust and (2) the mantle and (3) if the TF allows for plate decoupling. A weak brittle crust (1) enhances the fast propagation of deformation at shallow depths, which cannot be obtained in our modeling by crust ductile softening (contrary to Nikolaeva et al., 2010, in a passive margin setup). Moreover, the lowering of the crust brittle strength must be developed far away from the TF to allow for OPS. Although the minimum spatial scale of crust softening depends on plate age pair, we find that it is generally on the order of a hundred(s) of kilometers. Low brittle mantle strength (2) strongly promotes not only the OP plate bending and sinking by limiting the plate flexural rigidity but also YP deformations close to the plate boundary where asthenosphere upwelling focuses in mode 1. Finally, the TF must also be weak to enable mechanical decoupling between neighboring plates (3).
The amplitude of the preceding processes is regulated by five of the six physical parameters investigated in this study, as the activation energy does not actually affect OPS triggering (Fig. 3). Clearly, OPS cannot be simulated for a realistic set of physical parameters (Fig. 6a). To achieve OPS, the cursors controlling the plate mechanical structures have been tuned beyond the most realistic ranges (“yellow” domain, Fig. 3) for two parameters at least, and beyond reasonable values for at least one parameter (“red” domain, Fig. 6e to h). Nevertheless, combining different unlikely (“yellow”) parameter values (for ρTF and Lw) does help to achieve OPS for slightly less extreme mechanical conditions, as one parameter only has to be pushed up to the unrealistic (“red”) range (ρc, Fig. 6e). Note, however, that the plate age intervals showing OPS are then extremely narrow (Ay<3 Myr, Ao<25 Myr) and are not consistent with the three potential candidates of natural OPS.
5.1 Model limitations
5.1.1 2-D versus 3-D setup
Subduction initiation at a TF is here simplified using a 2-D process, whereas the fault strike-slip basically implies that it takes place as a 3-D phenomenon. For instance, the setting of Matthew and Hunter used to be a subduction-transform edge propagator (“STEP”) fault 2 Myr ago (Patriat et al., 2015), where 3-D mantle flows associated with the Australian plate subduction likely affected the TF structure and evolution, possibly favoring subduction initiation. This case exemplifies the role of 3-D far-field tectonics during subduction infancy (Table 1) and the potential role of deep mantle flows. Upward and downward mantle flows, even far away from the initiation site, have been shown to be able to initiate subduction in 2-D models (Lu et al., 2015; Baes and Sobolev, 2017). On the other hand, studies in 3-D by Boutelier and Beckett (2018) and Zhou et al. (2018) showed that subduction initiation depends on along-strike variations in plate structure. However, the strike-slip kinematics of an active TF have up to now, to our knowledge, never been taken into account in subduction initiation simulations. We show that a TF thermal state cooler than that modeled by a stair-step function does not hinder OPS. However, our results verify that in 2-D, without simulating the TF strike-slip, the process of spontaneous OPS has to occur at simulation onset to avoid the impeding effect of plate stiffening with further conductive cooling. Including the TF motion in 3-D experiments would compete against this strengthening effect in the area nearby the active spreading center.
Finally, one may argue that a 3-D setup would intrinsically facilitate OPS propagation at a transform fault. Plate sinking might initiate at the location where the offset in plate thickness is maximum (in the vicinity of a ridge spreading center) and then propagate away from this point (Zhou et al., 2018). However, as we focus on subduction initiation strictly speaking and not on subduction propagation, the use of a 2-D setup should remain meaningful to unravel the conditions of spontaneous sinking for a given plate age pair, considering apart the problem of the transform fault slip.
5.1.2 Free slip vs. free surface condition
Our results show that in most of our experiments showing OPS, the oceanic crust must be significantly weak (Fig. 6f–g). One may argue that the necessity of decoupling propagation close to the surface by shallow softening is related in our modeling to the absence of free surface (e.g., Crameri and Tackley, 2016). We test it by seeking for the threshold in the crustal brittle parameter allowing for OPS for one plate age pair 5 vs. 40 (sim. S26a in Table 3) as a function of the mechanical boundary condition imposed at the box top, either free-slip without vertical motion or free surface, mimicked by inserting a “sticky water” layer (see the Supplement Sect. S3 and Fig. S6). For the selected plate age pair, the threshold in crustal brittle parameter turns out to increase from ∼0.0025 without free surface to ∼0.0175. Hence, the necessary crust weakness that must be imposed to model OPS may be overestimated by a factor ∼7. This result agrees with previous studies showing that the free surface condition promotes the triggering of one-sided subduction in global mantle convection models (Crameri et al., 2012). Nevertheless, note that the threshold enabling OPS when the free surface is taken into account is still an unlikely value, since it is close to the limit of the extremely low range of the crust brittle parameter (“red” domain, Fig. 3).
5.1.3 Initiation swiftness and influence of elastic rheology
In a TF or fracture zone numerical setting without any external forcing, if subduction initiation has to occur, it can only take place at simulation onset because plate cooling results in a fast stiffening of oceanic lithospheres and, second, quickly attenuates the plate density offset (Hall and Gurnis, 2003). The process of subduction initiation modeled in our study systematically occurs very briefly after the simulation start, in less than 1 to 1.5 Myr. This quite “catastrophic” way of initiation has also been simulated in less than 0.8 Myr for other tectonic settings or triggering modes, such as passive margins (Nikolaeva et al., 2010; Marques and Kaus, 2016) or plume-induced mantle flows (Lu et al., 2015), using rheological conditions very similar to the ones assumed in this study. The initiation process is slightly slowed down but remains fast (duration <3 Myr) when the necessary weakness of the plate's stronger part is not fully imposed at simulation onset but progressively develops due to damaging or water-related weakening effects (Hall and Gurnis, 2003; Gurnis et al., 2004; Gerya et al., 2008; Dymkova and Gerya, 2013). Moreover, such unrealistically high velocities at plate sinking onset may result at least in part from the 2-D setup since, in a 3-D setup, the along-strike propagation slows down the initiation process; however, speeds of hinge retreat remain significantly high (between 13 and 20 cm yr−1 in Zhou et al., 2018). In addition, by neglecting elastic deformation, the amount of plate and interplate weakening required to trigger OPS may be excessive (Farrington et al., 2014). Nonetheless, the potential effect of elasticity on the OPS kinetics is not clear. On the one hand, including elasticity could slow down OPS initiation by increasing the threshold in the strength contrast, as aforementioned. On the other hand, the incipient subduction has been shown to remain as fast as modeled in the present study in elasto-visco-plastic models testing different modes of subduction initiation (Hall and Gurnis, 2003; Thielmann and Kaus, 2012; Baes et al., 2016). Previous modeling of subduction initiation including elasticity showed that the elastic flexure was a basic term of the subduction force balance (McKenzie, 1977; Hall and Gurnis, 2003; Gurnis et al., 2004). In our model, plate bending occurs by viscous (and brittle) deformations, as in numerous approaches to subduction that have successfully reproduced topographies and the strain and stress patterns observed in natural cases (e.g., Billen and Gurnis, 2005; Buffett, 2006). However, if elasticity might compete against subduction initiation by limiting the localization of lithospheric shearing, it may also help incipient subduction through the following release of stored elastic work (Thielmann and Kaus, 2012; Crameri and Tackley, 2016). Consequently, the threshold in mechanical parameters necessary to achieve OPS would probably be offset if elasticity was included.
5.1.4 Weakening of the oceanic mantle lithosphere
Our results show that OPS is strongly facilitated if the lithospheric mantle is weak. The reduction in mantle strength depends on the plate age pair and on other mechanical parameters, such as γm. A first-order estimate of the necessary mantle weakening is computed by comparing cases showing OPS to those in which OPS fails (Sect. S5 in the Supplement). The mantle weakening allowing for OPS is low to moderate for young plates and high plate age offsets (strength ratio ≤35), and larger when the plate age contrast is small (strength ratio ∼280). One may wonder if such mantle strength decreases are realistic. Different mechanisms of mantle weakening that we do not model may be discussed, such as (1) low-temperature plasticity (Goetze and Evans, 1979), that enhances the deformation of slab and plate base (Garel et al., 2014); (2) dislocation-accommodated grain-boundary sliding (GBS; Hansen et al., 2012); (3) grain-size reduction when diffusion linear creep is activated; or (4) fluid-related weakening. Peierls plasticity (1) limits the ductile strength in a high-stress regime at moderately high temperatures (≲1000 ∘C; Demouchy et al., 2013) but requires a high differential stress (>100 to 200 MPa) to be activated. Similarly, GBS power law regime (2) operates if stresses are >100 MPa, for large strain and low temperature (<800 ∘C; Drury, 2005). In our experiments, the simulated deviatoric stress is generally much lower than 100 MPa (Sect. S5 in the Supplement). For such low stresses, neither the Peierls nor the GBS creeps would be activated, hence we do not expect a major change in our results if they were implemented. Grain-size sensitive (GSS) diffusion linear creep (3) can strongly localize deformation at high temperature (e.g., Karato et al., 1986). In nature, GSS creep has been observed in mantle shear zones in the vicinity of a fossil ridge in Oman in contrast at rather low temperature (≲1000 ∘C; Michibayashi and Mainprice, 2004), forming very narrow shear zones (<1 km wide). However, the observed grain-size reduction of olivine is limited to ∼0.2–0.7 mm, which cannot result in a noticeable viscosity reduction. A significant strength decrease associated with GSS linear creep requires additional fluid percolation once shear localization is well developed within the subcontinental mantle (e.g., Hidas et al., 2016). The origin of such fluids at great depth within an oceanic young lithosphere is not obvious. Furthermore, GSS linear creep may only operate at stresses <10 MPa (Burov, 2011), which is not verified in our simulations (Sect. S5 in the Supplement).
In our models, mantle weakening is achieved by decreasing the mantle brittle parameter γm, to mimic the weakening effect of hydrated phases (4), such as talc or serpentine minerals (Sect. 2.5.1). Dymkova and Gerya (2013) show that the percolation of sea water down to ∼25 km depth during early OP deformation can enable the thick plate bending, assuming low porosity (≤2.5 %) and low mantle matrix permeability (10−21 m2) to significantly increase pore fluid pressure. In our approach, a high pore fluid pressure ratio (λ>0.5) is associated with a low mantle brittle parameter (γm<1, Fig. S1), for which OPS is modeled for a broad ranges of plate ages (Fig. 6g–h), in agreement with results by Dymkova and Gerya (2013). However, the low permeabilities assumed by Dymkova and Gerya (2013) are questioned by recent experiments of mantle hydration at ridge and of water percolation in a peridotite, and by estimates from a peridotite aquifer (Dewandel et al., 2004; Godard et al., 2013; Farough et al., 2016). These studies rather infer permeabilities between 10−19 and 10−16 m2, which would hamper high pore fluid pressures and, eventually, plate bending.
5.2 Comparison between OPS model requirements and natural cases
When analyzing the results of our parametric study (Sect. 4), the striking conclusion is that none of the realistic sets of parameters allowed for spontaneous subduction. Figure 6e, f, g, and h show that, even if one of the plates is extremely young (<7 Myr), the oceanic crust should be very dense (ρc=3300 kg m−3), as well as drastically weakened () at considerable distances from the TF (Lw≥50 km), to satisfy OPS necessary conditions. Assuming that such rather extreme conditions were fulfilled, OPS must develop (1) at simulation onset before plate cooling so that gravitational instability is maximal and (2) catastrophically in terms of the kinetics of the process, with sinking rates ≥15 up to 180 cm yr−1.
As depicted in Sect. 1, only two natural cases, IBM and Yap, attest to subduction initiation of an old oceanic plate beneath a young one at a TF, which later evolved into a mature subduction during the Cenozoic. The range of ages for both plates at time of initiation (Table 1) has been plotted in Fig. 6f, g and h. The plate ages at Yap subduction initiation are incompatible with the conditions of OPS inferred from our modeling results, suggesting that spontaneous subduction of the thicker plate is highly unlikely. Only IBM falls into the OPS domain based on age pairs at onset. There, the initial state of stress being unknown, as both plates edges have been consumed in subduction, it begs the question as to whether the old Pacific plate sunk spontaneously. Now, the question is as follows. To what extent are the rheological parameters and the characteristics of subduction initiation satisfied? Beyond the unrealistic values of crustal densities and brittle properties, the expected sinking rates and asthenosphere rise are high. The slab typically reaches a 200 km length within ∼1 Myr, so the remnants of the resulting “forearc crust” should be restricted to a very short time span. The argument of Arculus et al. (2015) that new findings of juvenile 52–48 Myr old oceanic crust in the Amami-Sankaku Basin that are far away from those already found in the IBM forearc (so-called “forearc basalts”) and the confirmation that the spontaneity of the subduction initiation and wide extent of the asthenosphere invasion was refuted by Keenan and Encarnación (2016) since younger juvenile oceanic crust cannot be used as a test for early uplift in presubduction initiation basement rocks. A second argument comes from the boninitic nature of the primary embryonic arc combining MORB and slab-derived hydrous fluid signatures (Ishizuka et al., 2006). Those boninites erupted between 51 and 44 Ma in the Bonin present arc and forearc (Ishizuka et al., 2011; Reagan et al., 2019) and between 48 and 43 Ma in the Mariana present forearc (Johnson et al., 2014). This time span appears incompatible with the swiftness of the processes required in our models. An alternative geodynamic scenario satisfying both the magmatic and the tectonic constraints has been proposed by Lallemand (2016). The kinematic change of Pacific plate motion following the Izanagi slab break off at approximately 60–55 Ma (Seton et al., 2015) created enabling conditions for convergence across a major TF or fracture zone. Compressive deformation progressively localizes until subduction starts at approximately 52 Ma. At approximately the same time, the occurrence of the Oki-Daitō plume has produced the splitting of the remnant arcs brought by the younger plate (Ishizuka et al., 2013). Oceanic basalts, called FABs (forearc basalts), spread along the axes perpendicular to the nascent trench (Deschamps and Lallemand, 2002, 2003). Boninites erupt as soon as hydrous fluids from the subducting plate metasomatize the shallow asthenosphere beneath the newly formed oceanic crust. Later, tectonic erosion along the IBM trench removes the frontal 200 km of the upper plate, exposing in the present forearc basalts and arc volcanics initially formed far from the trench.
As observed along the Hjort trench, subduction may start as soon as compressive tectonic forces are applied across a TF, but one should note that the subducting plate is the youngest there (Table 1; Abecassis et al., 2016). IBM and Yap cases likely fall in this “forced” category as mentioned above, but we lack direct field evidence, as they were both deeply eroded along their overriding edge.
5.3 Failure of old plate sinking is not excluded
Among the numerous parameter values tested in this study, especially those within reasonable (green) ranges, we have observed that most of them led to incipient subduction of either the young or the old plate but failed soon after (Fig. 6a to e). We have compiled in Table 1 several cases of potential subduction initiation along TFs or fracture zones that either failed (Romanche, Gagua, Barracuda, Tiburon, Saint Paul and Owen) or were just initiated, so we still ignore how it will evolve (Matthew and Hunter, Mussau, Macquarie, and Gorringe). The advantage of studying the aborted cases is that we still have access to the deformation that accompanied subduction initiation, and compression was always recorded in the early stages (see the references in Table 1). These incipient subduction areas are either restraining bends along transform faults or underwent changes in plate kinematics from strike-slip to transpression. A major limiting factor is the cooling of adjacent plates, as the distance from the spreading center or the plume increases, inhibiting their flexural capacities.
We perform a large set of 2-D thermomechanical simulations to study the conditions of spontaneous sinking of the older plate at a TF by investigating broad intervals of plate ages and by paying special attention to the mechanical parameter ranges allowing for OPS. OPS is simulated notably if the oceanic crust is dense and mechanically soft far away from the TF on both sides of the plate boundary. Our results confirm that the OP resistance to bending and the YP thickness are the most significant factors preventing OPS. Reducing the brittle properties of the oceanic lithosphere is thus the most efficient way to trigger OPS, compared to a softening by lowering the ductile strength, imposing a hot thermal anomaly or reducing the asthenospheric viscosity. When these extreme conditions are imposed, two processes of OPS are obtained, depending mainly on the assumed YP thickness. They can be summed up as (1) an OP rapid sinking that is decoupled from the YP kinematics and associated with a significant rise in the asthenosphere toward the subducting slab hinge and (2) a dragging of the YP by the sinking OP that is considered a two-sided subduction mode. In all cases, whatever the mode, OPS occurs in less than 1.5 Myr, that is, in an extremely short time span, and only if the initial mechanical setup is adjusted beyond reasonable limits for at least one key thermomechanical parameter. In addition, we find that neither the thermal structure and blurring of the transform fault area nor a plume head impact are able to affect OPS triggering in our modeling setup. Our study highlights the predominant role of a lithospheric weakening to enlarge the combination of plate ages allowing for OPS.
From the parametric study, we conclude that OPS cannot be simulated for a realistic combination of mechanical parameters. By comparing our modeling results to the most likely natural cases where spontaneous subduction at a TF has been invoked, we find that even though extreme mechanical conditions were assumed, the plate age setting at Yap should prevent OPS. Regarding the case of Izu–Bonin–Mariana, in addition to the weakness of geological arguments, the kinetics of subduction initiation, evidenced by geological records, is not compatible with the catastrophic mode systematically simulated in our experiments. We finally conclude that the spontaneous instability of the thick OP at a TF is an unlikely process of subduction initiation in modern Earth conditions.
The data that support the findings of this study are available upon request from the corresponding author, Diane Arcay (diane.arcay@umontpellier.fr).
The supplement related to this article is available online at: https://doi.org/10.5194/se-11-37-2020-supplement.
DA and SL designed the experiments, and DA and SA carried them out. DA, SL, and FG carried out the analysis and interpretation of the simulation results. DA and SL prepared the article with contributions from FG.
The authors declare that they have no conflict of interest.
Yann Heurtebize is acknowledged for his preliminary studies, during his masters degree in 2016, exploring the processes of OP subduction. This study benefited from stimulating and enlightening discussions about TF evolution and mantle physical properties with Marco Ligi, Marcia Maia, Daniele Brunelli, Marguerite Godard, Martin Patriat, and Andrea Tommasi. We are grateful to Stéphane Arnal, Fabrice Grosbeau, and Josiane Tack for the maintenance and development of the lab cluster of computing nodes on which all numerical experiments were performed. We are also grateful to Anne Delplanque, who drew Fig. 1. We warmly thank Ben Maunder and an anonymous reviewer for their thorough and very constructive comments that significantly improved the article, as well as Susanne Buiter for handling the editing.
This research has been supported by CNRS-INSU (National Institute of Universe Science) program “TelluS-SYSTER” (2015 and 2016).
This paper was edited by Susanne Buiter and reviewed by Ben Maunder and one anonymous referee.
Abecassis, S., Arcay, D., and Lallemand, S.: Subduction initiation at fracture zones: conditions and various modes, in: abstracts of the GeoMod conference, 17–20 October, p. 14, La Grande Motte, France, available at: http://geomod2016.gm.univ-montp2.fr/Home.html (last access: 20 December 2019), 2016. a, b
Adam, C., King, S., Vidal, V., Rabinowicz, M., Jalobeanu, A., and Yoshida, M.: Variation of the subsidence parameters, effective thermal conductivity, and mantle dynamics, Earth Planet. Sc. Lett., 426, 130–142, 2015. a
Afonso, J. C., Zlotnik, S., and Fernandez, M.: Effects of compositional and rheological stratifications on small-scale convection under the oceans: Implications for the thickness of oceanic lithosphere and seafloor flattening, Geophys. Res. Lett., 35, L20308, https://doi.org/10.1029/2008GL035419, 2008. a
Arcay, D.: Dynamics of interplate domain in subduction zones: influence of rheological parameters and subducting plate age, Solid Earth, 3, 467–488, https://doi.org/10.5194/se-3-467-2012, 2012. a
Arcay, D.: Modelling the interplate domain in thermo-mechanical simulations of subduction: Critical effects of resolution and rheology, and consequences on wet mantle melting, Phys. Earth Planet. Inter., 269, 112–132, https://doi.org/10.1016/j.pepi.2017.05.008, 2017. a, b
Arcay, D., Lallemand, S., and Doin, M.-P.: Back-arc Strain in Subduction Zones: Statistical Observations vs. Numerical Modelling, Geochem. Geophys. Geosyst., 9, Q05015, https://doi.org/10.1029/2007GC001875, 2008. a
Arculus, R. J., Ishizuka, O., Bogus, K. A., Gurnis, M., Hickey-Vargas, R., Aljahdali, M. H., Bandini-Maeder, A. N., Barth, A. P., Brandl, P. A., Drab, L., do Monte Guerra, R., Hamada, M., Jiang, F., Kanayama, K., Kender, S., Kusano, Y., Li, H., Loudin, L. C., Maffione, M., Marsaglia, K. M., McCarthy, A., Meffre, S., Morris, A., Neuhaus, M., Savov, I. P., Sena, C., Tepley III, F. J., van der Land, C., and Yogodzinski Zhang, G. M.: A record of spontaneous subduction initiation in the Izu-Bonin-Mariana arc, Nat. Geosci., 8, 728–733, https://doi.org/10.1038/ngeo2515, 2015. a, b
Baes, M. and Sobolev, S.: Mantle Flow as a Trigger for Subduction Initiation: A Missing Element of the Wilson Cycle Concept, Geochem. Geophys. Geosyst., 18, 4469–4486, https://doi.org/10.1002/2017GC006962, 2017. a, b
Baes, M., Gerya, T., and Sobolev, S. V.: 3-D thermo-mechanical modeling of plume-induced subduction initiation, Earth Planet. Sc. Lett., 453, 193–203, 2016. a, b
Behn, M. D., Lin, J., and Zuber, M. T.: Evidence for weak oceanic transform faults, Geophys. Res. Lett., 29, 60-1–60-4, https://doi.org/10.1029/2002GL015612, 2002. a
Billen, M. and Gurnis, M.: Constraints on subducting plate strength within the Kermadec trench, J. Geophys. Res., 110, B05407, https://doi.org/10.1029/2004JB003308, 2005. a
Bloomer, S.: Distribution and origin of igneous rocks from the landward slopes of the Mariana Trench: Implications for its structure and evolution, J. Geophys. Res., 88, 7411–7428, 1983. a
Bloomer, S. and Hawkins, J.: Petrology and geochemistry of boninite series volcanic rocks from the Mariana trench, Contrib. Mineral. Petrol., 97, 361–377, 1983. a
Bonatti, E., Ligi, M., Borsetti, A., Gasperini, L., Negri, A., and Sartori, R.: Lower Cretaceous deposits trapped near the equatorial Mid-Atlantic Ridge, Nature, 380, 518–520, 1996. a
Bousquet, R., Goffé, B., Henry, P., Le Pichon, X., and Chopin, C.: Kinematic, thermal and petrological model of the Central Alps: Lepontine metamorphism in the upper crust and eclogitisation of the lower crust, Tectonophysics, 273, 105–127, 1997. a
Boutelier, D. and Beckett, D.: Initiation of Subduction Along Oceanic Transform Faults: Insights From Three-Dimensional Analog Modeling Experiments, Front. Earth Sci., 6, 204, https://doi.org/10.3389/feart.2018.00204, 2018. a
Buck, W. R. and Parmentier, E.: Convection beneath young oceanic lithosphere: Implications for thermal structure and gravity, J. Geophys. Res.-Sol. Ea., 91, 1961–1974, 1986. a, b
Buffett, B.: Plate force du to bending at subduction zones, J. Geophys. Res., 111, B09405, https://doi.org/10.1029/2006JB004295, 2006. a
Burov, E. B.: Rheology and strength of the lithosphere, Mar. Petrol. Geol., 28, 1402–1443, https://doi.org/10.1016/j.marpetgeo.2011.05.008, 2011. a
Byerlee, J.: Friction of rocks, Pure Appl. Geophys., 116, 615–626, 1978. a, b
Cannat, M., Mamaloukas-Frangoulis, V., Auzende, J.-M., Bideau, D., Bonatti, E., Honnorez, J., Lagabrielle, Y., Malavieille, J., and Mevel, C.: A geological cross-section of the Vema fracture zone transverse ridge, Atlantic ocean, J. Geodynam., 13, 97–117, https://doi.org/10.1016/0264-3707(91)90034-C, 1991. a, b
Carlson, R. L. and Herrick, C. N.: Densities and porosities in the oceanic crust and their variations with depth and age, J. Geophys. Res.-Sol. Ea., 95, 9153–9170, https://doi.org/10.1029/JB095iB06p09153, 1990. a
Cazenave, A., Monnereau, M., and Gibert, D.: Seasat gravity undulations in the central Indian Ocean, Phys. Earth Planet. In., 48, 130–141, 1987. a
Christensen, U. R.: Convection with pressure- and temperature-dependent non-Newtonian rheology, Geophys. J. R. Astron. Soc., 77, 343–384, 1984. a
Christensen, U. R.: An Eulerian technique for thermomechanical modeling, J. Geophys. Res., 97, 2015–2036, 1992. a, b
Cloetingh, S., Wortel, R., and Vlaar, N. J.: On the initiation of subduction zones, Pure Appl. Geophys., 129, 7–25, https://doi.org/10.1007/BF00874622, 1989. a
Crameri, F. and Tackley, P. J.: Subduction initiation from a stagnant lid and global overturn: new insights from numerical models with a free surface, Prog. Earth Planet. Sci., 3, 30, https://doi.org/10.1186/s40645-016-0103-8, 2016. a, b, c
Crameri, F., Tackley, P., Meilick, I., Gerya, T., and Kaus, B.: A free plate surface and weak oceanic crust produce single-sided subduction on Earth, Geophys. Res. Lett., 39, L03306, https://doi.org/10.1029/2011GL050046, 2012. a
Demouchy, S., Tommasi, A., Ballaran, T. B., and Cordier, P.: Low strength of Earth’s uppermost mantle inferred from tri-axial deformation experiments on dry olivine crystals, Phys. Earth Planet. In., 220, 37–49, 2013. a
Deschamps, A. and Lallemand, S.: The West Philippine Basin: a Paleocene-Oligocene backarc basin opened between two opposed subduction zones., J. Geophys. Res., 107, 2322, https://doi.org/10.1029/2001JB001706, 2002. a, b, c
Deschamps, A. and Lallemand, S.: Geodynamic setting of Izu-Bonin-Mariana boninites, Geological Society, London, Special Publications, 219, 163–185, https://doi.org/10.1144/GSL.SP.2003.219.01.08, 2003. a, b
Deschamps, A., Monié, P., Lallemand, S., Hsu, S.-K., and Yeh, J.: Evidence for Early Cretaceous oceanic crust trapped in the Philippine Sea Plate, Earth Planet. Sci. Lett., 179, 503–516, 2000. a
Detrick, R. and Purdy, G.: The crustal structure of the Kane fracture zone from seismic refraction studies, J. Geophys. Res., 85, 3759–3777, 1980. a
Dewandel, B., Lachassagne, P., and Qatan, A.: Spatial measurements of stream baseflow, a relevant method for aquifer characterization and permeability evaluation. Application to a hard-rock aquifer, the Oman ophiolite, Hydrol. Process., 18, 3391–3400, https://doi.org/10.1002/hyp.1502, 2004. a
Doin, M.-P. and Henry, P.: Subduction initiation and continental crust recycling: the roles of rheology and eclogitization, Tectonophysics, 342, 163–191, 2001. a, b, c
Doin, M.-P., Fleitout, L., and McKenzie, D.: Geoid anomalies and the structure of continental and oceanic lithospheres, J. Geophys. Res., 101, 16119–16135, 1996. a
Doo, W.-B., Hsu, S.-K., Yeh, Y., Tsai, C., and Chang, C.: Age and tectonic evolution of the northwest corner of the West Philippine Basin, Mar. Geophys. Res., 36, 113–125, https://doi.org/10.1007/s11001-014-9234-8, 2015. a
Drury, M. R.: Dynamic recrystallization and strain softening of olivine aggregates in the laboratory and the lithosphere, Geological Society, London, Special Publications, 243, 143–158, 2005. a
Duarte, J.-A. C., Rosas, F., Terrinha, P., Schellart, W. P., Boutelier, D., Gutscher, M., and Ribeiro, A.: Are subduction zones invading the Atlantic? Evidence from the southwest Iberia margin, Geology, 41, 839–842, 2013. a
Dumoulin, C., Doin, M.-P., and Fleitout, L.: Heat transport in stagnant lid convection with temperature- and pressure-dependent Newtonian or non-Newtonian rheology, J. Geophys. Res., 104, 12759–12778, 1999. a, b
Dumoulin, C., Doin, M.-P., and Fleitout, L.: Numerical simulations of the cooling of an oceanic lithosphere above a convective mantle, Phys. Earth Planet. In., 125, 45–64, 2001. a
Dymkova, D. and Gerya, T.: Porous fluid flow enables oceanic subduction initiation on Earth, Geophys. Res. Lett., 40, 5671–5676, https://doi.org/10.1002/2013GL057798, 2013. a, b, c, d, e, f
Eakin, D., McIntosh, K., Van Avendonk, H., and Lavier, L.: New geophysical constraints on a failed subduction initiation: The structure and potential evolution of the Gagua Ridge and Huatung Basin, Geochem. Geophys. Geosyst., 16, 1–21, 2015. a
Escartín, J. and Cannat, M.: Ultramafic exposures and the gravity signature of the lithosphere near the Fifteen-Twenty Fracture Zone (Mid-Atlantic Ridge, 14∘–16.5∘ N), Earth Planet. Sci. Lett., 171, 411–424, 1999. a
Escartín, J., Hirth, G., and Evans, B.: Nondilatant brittle deformation of serpentinites: Implications for Mohr-Coulomb theory and the strength of faults, J. Geophys. Res., 102, 2897–2913, 1997. a
Farough, A., Moore, D. E., Lockner, D. A., and Lowell, R. P.: Evolution of fracture permeability of ultramafic rocks undergoing serpentinization at hydrothermal conditions: An experimental study, Geochem. Geophys. Geosyst., 17, 44–55, https://doi.org/10.1002/2015GC005973, 2016. a
Farrington, R. J., Moresi, L.-N., and Capitanio, F. A.: The role of viscoelasticity in subducting plates, Geochem. Geophys. Geosyst., 15, 4291–4304, https://doi.org/10.1002/2014GC005507, 2014. a
Fournier, M., Chamot-Rooke, N., Rodriguez, M., Huchon, P., Petit, C., Beslier, M., and Zaragosi, S.: Owen Fracture Zone: The Arabia–India plate boundary unveiled, Earth Planet. Sci. Lett., 302, 247–252, 2011. a
Fox, P. and Gallo, D.: A tectonic model for ridge-transition-ridge plate boundaries: Implications for the structure of oceanic lithosphere, Tectonophysics, 104, 205–242, https://doi.org/10.1016/0040-1951(84)90124-0, 1983. a
Fujiwara, T., Tamura, C., Nishizawa, A., Fujioka, K., Kobayashi, K., and Iwabuchi, Y.: Morphology and tectonics of the Yap Trench, Mar. Geophys. Res., 21, 69–86, 2000. a
Gaina, C. and Müller, D.: Cenozoic tectonic and depth/age evolution of the Indonesian gateway and associated back-arc basins, Earth Sci. Rev., 83, 177–203, https://doi.org/10.1016/j.earscirev.2007.04.004, 2007. a
Garel, F., Goes, S., Davies, D. R., Davies, J. H., Kramer, S. C., and Wilson, C. R.: Interaction of subducted slabs with the mantle transition-zone: A regime diagram from 2-D thermo-mechanical models with a mobile trench and an overriding plate, Geochem. Geophys. Geosyst., 15, 1739–1765, https://doi.org/10.1002/2014GC005257, 2014. a
Gerya, T., Connolly, J., and Yuen, D.: Why is terrestrial subduction one-sided?, Geology, 36, 43–46, 2008. a, b, c, d, e
Godard, M., Luquot, L., Andreani, M., and Gouze, P.: Incipient hydration of mantle lithosphere at ridges: A reactive-percolation experiment, Earth Planet. Sc. Lett., 371–372, 92–102, https://doi.org/10.1016/j.epsl.2013.03.052, 2013. a
Goetze, C. and Evans, B.: Stress and temperature in the bending lithosphere as constrained by experimental rock mechanics, Geophys. J. Int., 59, 463–478, https://doi.org/10.1111/j.1365-246X.1979.tb02567.x, 1979. a
Grose, C. J. and Afonso, J. C.: Comprehensive plate models for the thermal evolution of oceanic lithosphere, Geochem. Geophys. Geosyst., 14, 3751–3778, 2013. a, b, c
Gurnis, M., Hall, C., and Lavier, L.: Evolving force balance during incipient subduction, Geochem. Geophys. Geosyst., 5, Q07001, https://doi.org/10.1029/2003GC000681, 2004. a, b, c, d, e
Gutscher, M., Malod, J., Rehaul, J.-P., Contrucci, I., Klingelhoefer, F., Mendes-Victor, L., and Sparkman, W.: Evidence for active subduction beneath Gibraltar, Geology, 30, , 1071–1074, 2002. a
Hall, C. and Gurnis, M.: Catastrophic initiation of subduction following forced convergence across fra ctures zones, Earth Planet. Sci. Lett., 212, 15–30, https://doi.org/10.1016/S0012-821X(03)00242-5, 2003. a, b, c, d, e, f, g, h
Hall, C. E. and Gurnis, M.: Strength of fracture zones from their bathymetric and gravitational evolution, J. Geophys. Res.-Sol. Ea., 110, 1402, https://doi.org/10.1029/2004JB003312, 2005. a
Hansen, L. N., Zimmerman, M. E., and Kohlstedt, D. L.: The influence of microstructure on deformation of olivine in the grain-boundary sliding regime, J. Geophys. Res.-Sol. Ea., 117, 1402, https://doi.org/10.1029/2012JB009305, 2012. a
Harmon, N., Forsyth, D. W., and Weeraratne, D. S.: Thickening of young Pacific lithosphere from high-resolution Rayleigh wave tomography: A test of the conductive cooling model, Earth Planet. Sc. Lett., 278, 96–106, 2009. a
Hasterok, D.: A heat flow based cooling model for tectonic plates, Earth Planet. Sc. Lett., 361, 34–43, https://doi.org/10.1016/j.epsl.2012.10.036, 2013. a
Hawkins, J. and Batiza, R.: Metamorphic rocks of the Yap arc-trench system, Earth Planet. Sci. Lett., 37, 216–229, 1977. a
Haxby, W. F. and Weissel, J. K.: Evidence for small-scale mantle convection from Seasat altimeter data, J. Geophys. Res.-Sol. Ea., 91, 3507–3520, 1986. a
Hegarty, K. A. and Weissel, J. K.: Complexities in the Development of the Caroline Plate Region, Western Equatorial Pacific, in: The Ocean Basins and Margins, edited by: Nairn, A., Stehli, F., and Uyeda, S., Springer, Boston, MA, 7B, 277–301, https://doi.org/10.1007/978-1-4615-8041-6_6, 1988. a, b
Hegarty, K. A., Weissel, J. K., and Hayes, D. E.: Convergence at the Caroline-Pacific Plate Boundary: Collision and Subduction, chap. 18, pp. 326–348, American Geophysical Union (AGU), https://doi.org/10.1029/GM027p0326, 1983. a
Hickey-Vargas, R., Yogodzinski, G., Ishizuka, O., McCarthy, A., Bizimis, M., Kusano, Y., Savov, I., and Arculus, R.: Origin of depleted basalts during subduction initiation and early development of the Izu-Bonin-Mariana island arc: Evidence from IODP expedition 351 site U1438, Amami-Sankaku basin, Geochem. Cosmochem. Ac., 229, 85–111, https://doi.org/10.1016/j.gca.2018.03.007, 2018. a
Hidas, K., Tommasi, A., Garrido, C. J., Padrón-Navarta, J. A., Mainprice, D., Vauchez, A., Barou, F., and Marchesi, C.: Fluid-assisted strain localization in the shallow subcontinental lithospheric mantle, Lithos, 262, 636–650, https://doi.org/10.1016/j.lithos.2016.07.038, 2016. a
Hilde, T. and Lee, C.-S.: Origin and evolution of the west Philippine Basin: a new interpretation, Tectonophysics, 102, 85–104, https://doi.org/10.1016/0040-1951(84)90009-X, 1984. a
Hussong, D. and Uyeda, S.: Tectonic processes and the history of the Mariana Arc: a synthesis of the results of Deep Sea Drilling Project Leg 60, Initial Rep. Deep Sea Drill. Proj., 60, 909–929, 1981. a
Ishizuka, O., Kimura, J.-I., Li, Y. B., Stern, R. J., Reagan, M. K., Taylor, R. N., Ohara, Y., Bloomer, S. H., Ishii, T., Hargrove, U. S., and Haraguchi, S.: Early stages in the evolution of Izu-Bonin arc volcanism: New age, chemical, and isotopic constraints, Earth Planet. Sc. Lett., 250, 385–401, https://doi.org/10.1016/j.epsl.2006.08.007, 2006. a
Ishizuka, O., Tani, K., Reagan, M. K., Kanayama, K., Umino, S., Harigane, Y., Sakamoto, I., Miyajima, Y., Yuasa, M., and Dunkley, D. J.: The timescales of subduction initiation and subsequent evolution of an oceanic island arc, Earth Planet. Sc. Lett., 306, 229–240, https://doi.org/10.1016/j.epsl.2011.04.006, 2011. a, b
Ishizuka, O., Taylor, R. N., Ohara, Y., and Yuasa, M.: Upwelling, rifting, and age-progressive magmatism from the Oki-Daito mantle plume, Geology, 41, 1011–1014, https://doi.org/10.1130/G34525.1, 2013. a
Ishizuka, O., Hickey-Vargas, R., Arculus, R. J., Yogodzinski, G. M., Savov, I. P., Kusano, Y., McCarthy, A., Brandl, P. A., and Sudo, M.: Age of Izu-Bonin-Mariana arc basement, Earth Planet. Sc. Lett., 481, 80–90, https://doi.org/10.1016/j.epsl.2017.10.023, 2018. a
Johnson, J. A., Hickey-Vargas, R., Fryer, P., Salters, V., and Reagan, M. K.: Geochemical and isotopic study of a plutonic suite and related early volcanic sequences in the southern Mariana forearc, Geochem. Geophys. Geosyst., 15, 589–604, https://doi.org/10.1002/2013GC005053, 2014. a
Karato, S.-I., Paterson, M. S., and FitzGerald, J. D.: Rheology of synthetic olivine aggregates: Influence of grain size and water, J. Geophys. Res.-Sol. Ea., 91, 8151–8176, https://doi.org/10.1029/JB091iB08p08151, 1986. a
Keenan, T. and Encarnación, J.: Unclear causes for subduction, Nat. Geosci., 9, 338, https://doi.org/10.1038/ngeo2703, 2016. a, b
Korenaga, J.: Scaling of plate tectonic convection with pseudoplastic rheology, J. Geophys. Res.-Sol. Ea., 115, b11405, https://doi.org/10.1029/2010JB007670, 2010. a
Kuo, B.-Y., Chi, W.-C., Lin, C.-R., Chang, E.-Y., Collins, J., and Liu, C.-S.: Two-station measurement of Rayleigh wave phase velocities for the Huatung basin, the westernmost Philippine Sea, with OBS: implications for regional tectonics, Geophys. J. Int., 179, 1859–1869, https://doi.org/10.1111/j.1365-246X.2009.04391.x, 2009. a
Lallemand, S.: High rates of arc consumption by subduction processes: Some consequences, Geology, 23, 551–554, 1995. a
Lallemand, S.: Philippine Sea Plate inception, evolution and consumption with special emphasis on the early stages of Izu-Bonin-Mariana subduction, Prog. Earth Planet. Sci., 3, 15, https://doi.org/10.1186/s40645-016-0085-6, 2016. a, b, c, d, e
Lebrun, J.-F., Lamarche, G., and Collot, J.-Y.: Subduction initiation at a strike-slip plate boundary: the Cenozoic Pacific-Australian plate boundary, south of New Zealand, Geophys. Res. Lett., 108, 2453, https://doi.org/10.1029/2002JB002041, 2003. a
Leng, W. and Gurnis, M.: Subduction initiation at relic arcs, Geophys. Res. Lett., 42, 7014–7021, 2015. a, b
Lu, G., Kaus, B. J. P., Zhao, L., and Zheng, T.: Self-consistent subduction initiation induced by mantle flow, Terra Nova, 27, 130–138, https://doi.org/10.1111/ter.12140, 2015. a, b
Mackwell, S., Zimmerman, M., and Kohlstedt, D.: High-temperature deformation of dry diabase with applications to tectonics on Venus, J. Geophys. Res., 103, 975–984, 1998. a
Maia, M., Sichel, S., Briais, A., Brunelli, D., Ligi, M., Ferreira, N., Campos, T., Mougel, B., Brehme, I., Hémond, C., Motoki, A., Moura, D., Scalabrin, C., Pessanha, I., Alves, E., Ayres, A., and Oliveira, P.: Extreme mantle uplift and exhumation along a transpressive transform fault, Nat. Geosci., 9. 619–623, https://doi.org/10.1038/NGEO2759, 2016. a
Marques, F. and Kaus, B.: Speculations on the impact of catastrophic subduction initiation on the Earth System, J. Geodynam., 93, 1–16, https://doi.org/10.1016/j.jog.2015.09.003, 2016. a
Matsumoto, T. and Tomoda, Y.: Numerical simulation of the initiation of subduction at the fracture zone, J. Phys. Earth., 31, 183–194, https://doi.org/10.4294/jpe1952.31.183, 1983. a
McKenzie, D. P.: The Initiation of Trenches, in: Island Arcs, Deep Sea Trenches and Back-Arc Basins, edited by: Talwani, M. and Pitman, W. C., Maurice Ewing Series, 1, 57–61, American Geophysical Union (AGU), https://doi.org/10.1029/ME001p0057, 1977. a, b
Meckel, T., Mann, P., Mosher, S., and Coffin, M.: Influence of cumulative convergence on lithospheric thrust fault development and topography along the Australian-Pacific plate boundary south of New Zealand, Geochem. Geophys. Geosyst., 6, Q09010, https://doi.org/10.1029/2005GC000914, 2005. a, b
Michibayashi, K. and Mainprice, D.: The role of pre-existing mechanical anisotropy on shear zone development within oceanic mantle lithosphere: an example from the Oman ophiolite, J. Petrol., 45, 405–414, 2004. a
Moore, D., Lockner, D., Tanaka, H., and Iwata, K.: The coefficient of friction of chrysotile gouge at seismogenic depths, Int. Geol. Rev., 46, 385–398, 2004. a
Morency, C. and Doin, M.-P.: Numerical simulations of the mantle delamination, J. Geophys. Res., 109, 3410, https://doi.org/10.1029/2003JB002414, 2004. a
Morency, C., Doin, M.-P., and Dumoulin, C.: Three-dimensional numerical simulations of mantle flow beneath mid-ocean ridges, J. Geophys. Res.-Sol. Ea., 110, B11407, https://doi.org/10.1029/2004JB003454, 2005. a
Mortimer, N., Gans, P. B., Palin, J., Herzer, R. H., Pelletier, B., and Monzier, M.: Eocene and Oligocene basins and ridges of the Coral Sea-New Caledonia region: Tectonic link between Melanesia, Fiji, and Zealandia, Tectonics, 33, 1386–1407, https://doi.org/10.1002/2014TC003598, 2014. a
Mueller, S. and Phillips, R. J.: On the initiation of subduction, J. Geophys. Res.-Sol. Ea., 96, 651–665, 1991. a
Natland, J. and Tarney, J.: Petrologic evolution of the Mariana Arc and back-arc basin system – a synthesis of drilling results in the South Philippine Sea, Initial Reports of the Deep Sea Drilling Project, 60, 877–908, 1981. a, b
Nikolaeva, K., Gerya, T. V., and Connolly, J. A.: Numerical modelling of crustal growth in intraoceanic volcanic arcs, Phys. Earth Planet. In., 171, 336–356, https://doi.org/10.1016/j.pepi.2008.06.026, 2008. a
Nikolaeva, K., Gerya, T. V., and Marques, F. O.: Subduction initiation at passive margins: numerical modeling, J. Geophys. Res., 115, B03406, https://doi.org/10.1029/2009JB006549, 2010. a, b, c, d, e
Parsons, B. and Sclater, J. G.: An analysis of the variation of ocean floor bathymetry and heat flow with age, J. Geophys. Res., 82, 803–827, 1977. a
Patriat, M., Pichot, T., Westbrook, G., Umber, M., Deville, E., Bénard, F., Roest, W., Loubrieu, B., and the Antiplac cruise party: Evidence for Quaternary convergence between the North American and South American plates, east of the Lesser Antilles, Geology, 39, 979–982, 2011. a
Patriat, M., Collot, J., Danyushevsky, L., Fabre, M., Meffre, S., Falloon, T., Rouillard, P., Pelletier, B., Roach, M., and Fournier, M.: Propagation of back-arc extension into the arc lithosphere in the southern New Hebrides volcanic arc, Geochem. Geophys. Geosyst., 16, 3142–3159, https://doi.org/10.1002/2015GC005717, 2015. a, b, c, d
Pichot, T., Patriat, M., Westbrook, G., Nalpas, T., Gutscher, M., Roest, W., Deville, E., Moulin, M., Aslanian, D., and Rabineau, M.: The Cenozoic tectonostratigraphic evolution of the Barracuda Ridge and Tiburon Rise, at the western end of the North America – South America plate boundary zone, Mar. Geol., 303–306, 154–171, https://doi.org/10.1016/j.margeo.2012.02.001, 2012. a
Qiuming, C.: Fractal density and singularity analysis of heat flow over ocean ridges, Sci. Rep.-UK, 6, 19167, https://doi.org/10.1038/srep19167, 2016. a
Raleigh, C. and Paterson, M.: Experimental deformation of serpentinite and its tectonic implications, J. Geophys. Res., 70, 3965–3985, 1965. a
Ranalli, G.: Rheology of the Earth, Chapman and Hall, London, 2nd edn., 1995. a, b
Reagan, M. K., Heaton, D. E., Schmitz, M. D., Pearce, J. A., Shervais, J. W., and Koppers, A. A.: Forearc ages reveal extensive short-lived and rapid seafloor spreading following subduction initiation, Earth Planet. Sc. Lett., 506, 520–529, https://doi.org/10.1016/j.epsl.2018.11.020, 2019. a
Ribe, N. and Christensen, U.: Three-dimensional modeling of plume-lithosphere interaction, J. Geophys. Res., 99, 699–682, 1994. a, b
Rocchi, V., Sammonds, P. R., and Kilburn, C. R.: Flow and fracture maps for basaltic rock deformation at high temperatures, J. Volcanol. Geoth. Res., 120, 25–42, https://doi.org/10.1016/S0377-0273(02)00343-8, 2003. a
Sdrolias, M. and Müller, R.: Controls on back-arc basin formation, Geochem. Geophys. Geosyst., 7, Q04016, https://doi.org/10.1029/2005GC001090, 2006. a
Searle, R.: Multiple, closely spaced transform faults in fast-slipping fractures zones, Geology, 11, 607–610, 1983. a, b
Seton, M., Flament, N., Whittaker, J., Müller, R., Gurnis, M., and Bower, D.: Ridge subduction sparked reorganization of the Pacific plate-mantle system 60–50 million years ago, Geophys. Res. Lett., 42, 1732–1740, https://doi.org/10.1002/2015GL063057, 2015. a
Sibuet, J.-C., Hsu, S.-K., Le Pichon, X., Le Formal, J.-P., Reed, D., Moore, G., and Liu, C.-S.: East Asia plate tectonics since 15 Ma: constraints from the Taiwan region, Tectonophysics, 344, 103–134, 2002. a
Stein, S. and Stein, S.: A model for the global variation in oceanic depth and heat flow with lithospheric age, Nature, 359, 123–129, 1992. a
Stern, R. and Bloomer, S.: Subduction zone infancy: examples from the Eocene Izu- Bonin-Mariana and Jurassic California arcs, Geol. Soc. Am. Bull., 104, 1621–1636, https://doi.org/10.1130/0016-7606(1992)104<1621:SZIEFT>2.3.CO;2, 1992. a, b
Stern, R. J. and Gerya, T.: Subduction initiation in nature and models: A review, Tectonophysics, 746, 173–198, https://doi.org/10.1016/j.tecto.2017.10.014, 2018. a, b, c, d
Tesei, T., Harbord, C. W. A., De Paola, N., Collettini, C., and Viti, C.: Friction of Mineralogically Controlled Serpentinites and Implications for Fault Weakness, J. Geophys. Res.-Sol. Ea., 123, 6976–6991, https://doi.org/10.1029/2018JB016058, 2018. a
Tetreault, J. L. and Buiter, S. J. H.: Future accreted terranes: a compilation of island arcs, oceanic plateaus, submarine ridges, seamounts, and continental fragments, Solid Earth, 5, 1243–1275, https://doi.org/10.5194/se-5-1243-2014, 2014. a
Thielmann, M. and Kaus, B. J. P.: Shear heating induced lithospheric-scale localization: does it result in subduction?, Earth Planet. Sci. Lett., 359/360, 1–13, https://doi.org/10.1016/j.epsl.2012.10.002, 2012. a, b, c
Tompkins, M. J. and Christensen, N. I.: Effects of pore pressure on compressional wave attenuation in a young oceanic basalt, Geophys. Res. Lett., 26, 1321–1324, https://doi.org/10.1029/1999GL900216, 1999. a
Tortella, D., Torne, M., and Perez-Estaun, A.: Geodynamic Evolution of the Eastern Segment of the Azores-Gibraltar Zone: The Gorringe Bank and the Gulf of Cadiz Region, Mar. Geophys. Res., 19, 211–230, https://doi.org/10.1023/A:1004258510797, 1997. a
Turcotte, D. and Schubert, G.: Geodynamics: Applications of continuum physics to geological problems, Cambridge University Press, New York, second edn., 1982. a, b, c
Ueda, K., Gerya, T., and Sobolev, S. V.: Subduction initiation by thermal–chemical plumes: Numerical studies, Phys. Earth Planet. In., 171, 296–312, https://doi.org/10.1016/j.pepi.2008.06.032, 2008. a, b, c
Uyeda, S. and Kanamori, H.: Back-arc opening and the mode of subduction zones, J. Geophys. Res., 84, 1049–1062, 1979. a
van Keken, P., King, S., Schmeling, H., Christensen, U., Neumeister, D., and Doin, M.-P.: A comparison of methods for the modeling of thermochemical convection, J. Geophys. Res., 102, 22477–22495, 1997. a
Violay, M., Gibert, B., Mainprice, D., Evans, B., Dautria, J.-M., Azais, P., and Pezard, P.: An experimental study of the brittle-ductile transition of basalt at oceanic crust pressure and temperature conditions, J. Geophys. Res.-Sol. Ea., 117, B03213, https://doi.org/10.1029/2011JB008884, 2012. a, b
Whattam, S. A. and Stern, R. J.: Late Cretaceous plume-induced subduction initiation along the southern margin of the Caribbean and NW South America: The first documented example with implications for the onset of plate tectonics, Gond. Res., 27, 38–63, https://doi.org/10.1016/j.gr.2014.07.011, 2015. a
Wilks, K. and Carter, N.: Rheology of some continental lower crustal rocks, Tectonophysics, 182, 57–77, 1990. a
Wolfson-Schwehr, M., Boettcher, M. S., McGuire, J. J., and Collins, J. A.: The relationship between seismicity and fault structure on the Discovery transform fault, East Pacific Rise, Geochem. Geophys. Geosyst., 15, 3698–3712, https://doi.org/10.1002/2014GC005445, 2014. a
Yongsheng, Z., Changrong, H., Xiaoge, H., Juan, S., Zunan, S., and Hua, K.: Rheological Complexity of Mafic Rocks and Effect of Mineral Component on Creep of Rocks, Earth Sci. Front., 16, 76–87, 2009. a
Zhou, X., Li, Z.-H., Gerya, T. V., Stern, R. J., Xu, Z., and Zhangi, J.: Subduction initiation dynamics along a transform fault control trench curvature and ophiolite ages, Geology, 46, 607–610, https://doi.org/10.1130/G40154.1, 2018. a, b, c, d, e
Zhu, G., Gerya, T. V., Yuen, D. A., Honda, S., Yoshida, T., and Connolly, J. A. D.: Three-dimensional dynamics of hydrous thermal-chemical plumes in oceanic subduction zones, Geochem. Geophys. Geosyst., 10, Q11006, https://doi.org/10.1029/2009GC002625, 2009. a
Zhu, G., Gerya, T. V., Honda, S., Tackley, P. J., and Yuen, D. A.: Influences of the buoyancy of partially molten rock on 3-D plume patterns and melt productivity above retreating slabs, Phys. Earth Planet. In., 185, 112–121, https://doi.org/10.1016/j.pepi.2011.02.005, 2011. a
spontaneouslithospheric collapse at a transform fault (TF) by performing a large study of conditions allowing instability of the thicker plate using 2-D thermomechanical simulations. Spontaneous subduction is modelled only if extreme mechanical conditions are assumed. We conclude that spontaneous collapse of the thick older plate at a TF evolving into mature subduction is an unlikely process of subduction initiation at modern Earth conditions.
spontaneouslithospheric collapse at a transform...